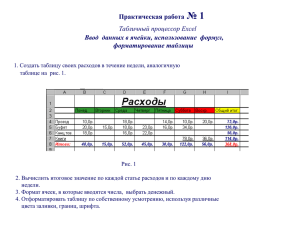
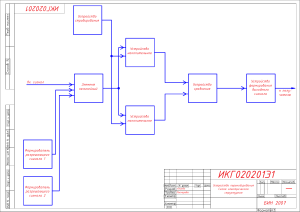
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ МЕДИКОВ И БИОЛОГОВ
МЕТОДЫ СПЕКТРАЛЬНОЙ ДЕКОМПОЗИЦИИ
ХРОНОКАРДИОГРАММ
ВВЕДЕНИЕ
Несмотря на успешное использование методов анализа вариабельности ритма в медицинской
практике, в данной области науки отсутствуют общепризнанные международные стандарты и
рекомендации: ни для выбора оптимальных методов, ни для выбора адекватных параметров,
ни даже устойчивые диапазоны для корректной интерпретации полученных результатов [??].
Причём очевидному желанию сравнивать промежуточные результаты анализа, проведённого
на продуктах от разных производителей, но придерживающихся схожих подходов, мешает то,
что по большей части все программные реализации численных методов являются «чёрными
ящиками» и обнаружить причину, по которой они, при заявленном совпадении их подходов,
выдают порой существенно отличающиеся результаты, крайне сложно не только для медиков
или биологов, но и для математиков, хорошо представляющих работу спектральных методов.
Ввиду такого положения дел кажется полезным издание методического пособия, призванного
ликвидировать разрыв между академическим представлением о методах анализа сердечного
ритма и пониманием специфики отдельных реализаций, уделяя особенное внимание именно
тем факторам, из-за которых и возникают критические изменения конечных результатов, как
это и будет продемонстрировано ниже с примерами и объяснениями.
Изложение материала данного пособия рассчитано на самый широкий круг читателей, кто в
общих чертах знаком с электронными таблицами и имеет возможность повторить расчёты в
любой среде, совместимой с MS Excel. Причём установки самой среды на свой компьютер не
потребуется при наличии современного браузера и доступа во всемирную сеть Интернет, где
существует целый ряд «облачных» решений для работы с подобными таблицами [??, ??, ??].
Доступ в Интернет понадобится также для загрузки ритмограмм из общедоступных тестовых
коллекций [??]. Таким образом, при написании методического пособия удалось максимально
снизить как необходимый уровень начальной подготовки читателя, так и все технические, а
также программные требования к устройствам, выполняющим расчёты, фактически, сведя их
к наличию любого современного компьютера общего назначения. Однако поясним, что даже
полное и успешное овладение навыками подобных расчётов и анализа вариабельности ритма
«на коленке» никоим образом не должны восприниматься как некая замена соответствующим
программным продуктам, имеющимся на рынке, так как последние гораздо более удобны для
автоматизации анализа и визуализации результатов. Напротив, освоение нового для себя вида
полу-автоматической обработки данных и анализа ритмограмм даст ясное представление об
используемых на практике инструментах, а также даст возможность проверки сомнительных
результатов анализа и «обкатывания» новых идей, которые можно сначала опробовать самим
и уже позже порекомендовать для включения в новую версию программного продукта. Таким
образом можно снизить уровень неопределённости для лиц, принимающих важное решение,
от чего может зависеть жизнь пациента. Таким образом, получим исследователей, не зажатых
между двумя «чёрными ящиками» – между скрытыми процессами в человеческом организме
и столь же скрытыми расчётами «под капотом» имеющегося программного инструментария –
сделав по прочтению этого пособия хотя бы один из них абсолютно прозрачным и понятным.
ПОЛУЧЕНИЕ РИТМОГРАММ
История вопроса
Первые методы диагностики здоровья при заболеваниях сердечно-сосудистой системы были
основаны исторически на самом простом способе – оценке частоты сердечных сокращений
(ЧСС), осуществляемой вручную ещё с самой древности, путём подсчёта пульс-ритмических
колебаний стенок артерий за определённый интервал времени (традиционно они измеряются
как удары/минуту, хотя должны измеряться в Гц согласно СИ). Такие методы, основанные на
пульсометрии, получили широкое распространение в виду простоты измерения ритма, т. к.
он легко прощупывается пальцами, если их расположить на запястье у основания большого
пальца, т. е. по ходу лучевой артерии. Другим немаловажным фактором, сыгравшем в пользу
исторического развития таких способов диагностики, особенно в рамках восточной народной
медицины, являются культурные особенности, не позволяющие проведение врачом полного
осмотра пациента другого пола.
Вообще, пульсовая диагностика включает в себя рассмотрение множества характеристик, не
только ЧСС, и их число росло за долгую историю развития на западе (от грека Герофила до
перса Авиценны) и на востоке (от китайца Бянь Цао до индийца Нагарджуна). Однако здесь
рассматриваются только оценки, связанные с ритмом сердца или, точнее, с вариабельностью
сердечных сокращений. Интересно отметить, что несмотря на отбрасывание массива важных
характеристик пульса, с помощью одной вариабельности ЧСС можно рассчитать важнейшие
оценки, чья достоверность подтверждена и в ходе клинических исследований, и на практике.
Причём ряд оценок возможно провести и вручную, например, пробу Руфье, которая известна
всем с детства и заключается в расчёте индекса Руфье-Диксона на основании двух-трёх ЧСС,
измеренных до и после физической нагрузки.
В данном пособии рассматриваются только оценки, получаемые на основании спектрального
анализа вариабельности сердечного ритма, рассчитываемые при помощи численных методов
при обработке крупных объёмов данных на ЭВМ, что позволяет извлечь из биомедицинских
данных глубокие, скрытые закономерности, повысив точность и ускорив вычисления, теперь
протекающие не в ручном, а в полуавтоматическим режиме. С другой стороны, если на ЭВМ
обработка данных происходит как многостадийный процесс, реализующий некую сложную
последовательную систему расчёта, то надёжность конечных результатов окажется в прямой
зависимости от надёжности всех стадий расчёта, накапливая всё новые и новые неточности и
ошибки на каждом этапе вычислений. Здесь же, в первой части пособия, рассмотрены самые
первые неточности, возникающие уже на стадии непосредственного получения ритмограмм.
Получение КИГ из ЭКГ
Очевидно, что достаточно крупные объёмы биомедицинских данных могут быть получены
только лишь инструментальными способами когда требуется позиционирование пика ударов
сердца с высокой точностью, вплоть до сотых и тысячных долей секунды. Причём, даже если
бы врач был способен фиксировать удары сердца с такой точностью по времени, то и тогда
установить вручную точное позиционирование пика сложно по причине его «размытости».
Исследуя артериальное давление легко фиксировать биения, но сложно точно определять, где
находились начало, конец или максимум для каждого из ударов сердца. Однако изобретение
электричества, давшее новые инструменты исследователям из самых разных областей науки,
не обошло вниманием и проблему инструментальной диагностики в области вариационной
пульсометрии. Оказалось, изменения электрических полей, образующихся при работе сердца,
возможно наблюдать и записывать – так возникла электрокардиография (ЭКГ), на графиках
которой легко различимы моменты пикового напряжения и значит, если сделать естественное
допущение, что частота таких пиков соответствует ЧСС, получим инструмент высокоточной
регистрации ЧСС через ЭКГ.
Все ЭКГ-аппараты основаны на одном биофизическом явлении: если электроды вольтметра
приложить к особым точкам на теле человека (т. н. отведениям), стрелка укажет на величину
электростатического потенциала, возникающего на этом участке в данный момент, причём
стрелка будет совершать колебания вслед за биением сердца. Далее несложно придти к идее
преобразования элеткромеханического вольтметра в самописец с протяжной лентой, заставив
стрелку измерительного прибора оставлять след на размеченной миллиметровой бумаге – так
удалось предложить первый способ записи изменений электрического поля (рис. ??), которые
неизменно происходят при сокращениях сердца. На рисунке легко видеть, что такие сигналы
состоят из схожих повторяющихся всплесков и зон относительного спокойствия между ними.
Профили всплесков специфичны для каждого отведения, но в каждом из них традиционно [?]
выделяются 5 характерных локальных экстремумов, помечаемых последовательно буквами:
P, Q, R, S, T; причём так, чтобы на точку R приходился глобальный максимум всего всплеска
(рис.?). Очевидно, наиболее чёткими, а значит наименее «размытыми», являются экстремумы
в R точках, что сделало их первыми кандитатами на роль главного маркера сердечного ритма,
а впоследствии, с развитием техники, паузы между сокращениями сердца стали вычисляться
именно как интервалы времени между соседними R пиками. Значения длин RR-интервалов, в
привязке к моменту их регистрации, называют кардиоинтервалограммой (КИГ) [??] (или же
ритмограммой [??]) и именно эти данные обычно используются для оценки вариабельности
сердечного ритма (ВСР). В общих чертах такой подход получения ритмограмм не изменился
и по сей день, но конечно, современные методы вычисления RR-интервалов уже не требует
применения миллиметровки и линейки, т. к. вместо аналоговых ЭКГ-аппаратов используются
ЭВМ, оцифровывающие ЭКГ с заданной частотой дискретизации (от 100 до 1000 Гц) [??].
Ещё раз напомним: предполагается, что сердечный ритм есть некий колебательный процесс,
а интервалам RRt соответствуют периоды колебаний, отмеченные в момент времени t, но т. к.
период колебания есть величина обратная к частоте колебания, легко придти к взаимосвязи
RR-интервалов и частоты сердечный сокращений. Ввиду этого последовательность обратных
величин: 1/RRt, иногда называют «мгновенными» ЧСС [?], что, в некотором роде, объединяет
современные и ранние научные знания в области диагностики здоровья человека по ритму
сердца. Заметим, что как и в древности, при переходе к КИГ, от сигнала ЭКГ остаётся крайне
мало первоначальной общей информации, но и её достаточно для проведения диагностики.
Доступность данных
Продемонстрируем процесс получения ритмограмм из ЭКГ, воспользовавшись коллекциями
данных из общедоступных источников, например, полученными нашими коллегами из ННГУ
им. Н. И. Лобачевского [??]. Но прежде определимся с форматом файлов, используемым для
хранения оцифрованных биомедицинских сигналов [??], т. к. часто форматы несовместимы
между собой и слишком специфичны для открытия одним универсальным редактором, а это
предполагает установку программного обеспечения (ПО) под каждый отдельный формат [??].
Многие из этих ПО являются проприетарными, но как оговаривалось выше, следует избегать
использования любого платного ПО, кроме Excel или других совместимых с ним редакторов
электронных таблиц. Такое условие раньше показалось бы чересчур жёстким, но не сегодня,
когда появилась масса облачных решений, превративших современные браузеры из простого
веб-обозревателя в «швейцарский нож» на все случаи жизни. Благодаря браузерам целый ряд
задач уже не требует установки специального ПО, в том числе и задача графического вывода
ЭКГ-сигналов и преобразования в табличный вид, с чем легко справляется веб-приложение
LightWAVE от Лаборатории вычислительной физиологии Массачусетского технологического
института (МТУ), которое доступно каждому посетителю на сайте PhysioNet.org. На том же
сайте размещена и коллекция ННГУ [??], что упростит дальнейшую демонстрацию процесса.
Коллекция ННГУ представлена в формате WaveForm-DataBase (WFDB), также
разработанном в МТУ, причём задолго до популяризации новых подходов по сериализации
данных в файлах, до введения метафайлов, позволяющих в составе единого файла хранить
как данные, так и их описания (метаданные). Поэтому анкетные данные пациентов, время
снятия ЭКГ и так далее, согласно формату WFDB, указываются в отдельном файле-заголовке
с расширением hea (от англ. header), а оцифрованные ЭКГ-сигналы пишутся в файл-данных
с расширением dat (от англ. data). Причём файлы заголовков представлены в текстовом
формате и просматриваются любым текстовым редактором, а в файлах данных хранятся
значения в компактном бинарном виде, который невозможно открыть напрямую из Excel. По
сути, dat файл является матрицей неких значений, чей размер и компьютерный формат
представления чисел указаны в файле-заголовке. Такие файлы часто называются «сырыми»,
т. е. записанными с устройства как есть и требующими дополнительной обработки, но даже
их не преобразовать в текстовый вид без специального ПО или, как альтернатива, вебприложения LightWAVE.
В таком случае процесс получения ритмограмм можно начать с открытия сайта physionet.org
в любом современном браузере и в строке поиска Search ввести запрос “lobachevsky university
electrocardiography”, а затем на странице выдачи результатов поиска найти публикацию от 19
января 2021 года, под которой находится типовая ссылка Visualize waveforms – она уже ведёт
к автоматическому открытию текущей коллекции в приложении LightWAVE. После перехода
в выпадающем меню Record следует выбрать любой из 200 наборов, например, “data/1”, что
приведёт к переключению на вкладку View/edit, где в графическом виде отобразятся сигналы
ЭКГ от всех указанных отведений. Так как для импортирования в Excel требуются табличные
данные, далее следует переключиться на вкладку Tables, где следует отметить флажки "View
annotations as text" и "View signals as text", затем нажать кнопку “↴”, после чего по странице
ниже возникнут дополнительные разделы, помимо Summary (англ. сводка): Annotations (англ.
аннотации) и Signals (англ. сигналы). В разделе Signals расположена текстовая таблица – её
следует выделить (см. рис. ??), скопировать и вставить в новую электронную таблицу.
Доступность ПО
Во всех примерах пособия далее для определённости будет предполагаться, что используется
конкретный редактор электронных таблиц, а именно веб-приложение Таблицы от облачного
сервиса Яндекс.Диск, доступное всем пользователям бесплатной службы Яндекс.Почта. Для
создания новой таблицы следует перейти на сайт disk.yandex.ru, после чего последовательно
нажать кнопки «Создать» и «Таблицу» (см. рис ??). Такой выбор редактора таблиц позволит
совершенно избавиться от необходимости установки какого-либо ПО на ПК (персональный
компьютер), планшет и смартфон, ограничившись исключительно стандартными средствами,
поставляемыми по умолчанию на любую платформу и операционную систему (ОС).
Обратим внимание, если строки текста скопированы с веб-сайта, то для их вставки в таблицу
рекомендуется использовать сочетание клавиш [Ctrl+Shift+V], а не более привычное [Ctrl+V].
Иначе строки текста, скопированные из веб-документов, будут иметь разный размер шрифта
и каждая вставка текста будет вызывать длительные паузы («подвисания»), необходимые для
пересчёта высоты строк таблицы. Во избежание этого эффекта следует очищать вставляемый
текст от форматирования, что можно сделать не одним способом: 1) продвинутые редакторы
автоматически удаляют форматирование перед вставкой, если нажаты клавиши Ctrl+Shift+V;
2) этого же эффекта можно добиться и через контекстное меню, если нажать правую кнопку
мыши и выбрать опцию «Параметры вставки → Значения», или же, в более ранних версиях,
пункт «Специальная вставка...»; 3) наконец, самый раний, проверенный способ предполагает
промежуточное копирование фрагментов в любой редактор текста (старого образца), который
«не понимает» стилевые оформления текста и отбрасывает их, после чего этот «очищенный»
текст можно снова скопировать и вставить теперь уже в редактор таблиц.
Примечание: в качестве текстового редактора старого образца можно предложить Блокнот –
стандартное приложение ОС Windows, вызвать которое можно сочетанием клавиш [Win+R],
после чего следует ввести слово “notepad” в текстовое поле и нажать кнопку “OK”. В таком
случае, если выбран третий способ промежуточного копирования, все действия упрощаются
до привычных Ctrl+A,Ctrl+C для копирования всего текста со страницы и Ctrl+V для вставки
текста в Блокнот, где выделять фрагменты таблиц станет даже проще, чем на веб-сайте.
После вставки строк в таблицу в первую очередь следует проверить выровнены ли числа по
правому краю ячеек. Если нет, используемый редактор локализован для региона, где дробные
части чисел принято отделять десятичной запятой, а значит значения с англоязычного сайта,
где используется десятичная точка, будут ошибочно восприниматься редактором как строки
текста, выравниваясь по левому краю ячейки. Существует масса способов исправления такой
ошибки, например, с помощью прямой замены всех точек на запятые, что легко организовать
в автоматическом режиме, вызвав пункт меню «Правка →Найти и заменить...», затем в поле
«Найти» ввести одну точку, а в поле «Заменить на» одну запятую, после чего нажать кнопку
«Заменить все» (см. рис ??).
Ручная обработка данных
Итак в первой колонке таблицы указаны моменты времени, когда регистрируется напряжение
на каждом из отведений. Величина электрического напряжения, измеренная в милливольтах,
указана в текущей строке в ячейке столбца, заголовок которого содержит соответствующий
код отведения. При этом динамика напряжения в таблице в точности совпадает с данными на
сайте, но первые ячейки столбца Time равны нулевому отсчёту времени, что не соответствует
действительности. Так происходит из-за более грубого представления времени в редакторах
таблиц, в сравнении с профессиональными приложениями, но эту проблему легко разрешить,
если значения в формате времени заменить на отсчёты времени в секундах, представленные
дробными числами двойной точности [?]. Это несложно осуществить при знании интервала
выборки (промежутка времени между соседними точками регистрации сигнала), т. е. шага по
времени, который легко вычислить как величину, обратную к частоте дискретизации, что
указано на сайте в разделе Summary в поле Clock frequency. Итак, имея 500 отсчётов сигнала в
секунду, получим интервал между отсчётами: 1/500 = 0,002 с., что и будет использовано ниже
для построения равномерной решётки, общей для всех ЭКГ-сигналов.
Построение корректной временнόй сетки начнём с чистого листа, точнее, на новом листе, для
создания которого следует щёлкнуть по значку «+» (плюс), находящемуся внизу экрана, сразу
за ярлычком «Лист1». После этого скопируем столбец B на новый Лист2. Выделить столбец
целиком можно кликнув по названию столбца на координатной панели, после чего следует
скопировать (Ctrl+C) и вставить (Ctrl+V) его на Лист2, выделив перед этим ячейку B1. Далее
в ячейки A1, A2 и A3 соответственно записывается: «Время», «(мс)» и «0», задающие начало
отсчёта времени. Начиная с A4 следует указывать расчётное время, полученное на основании
известного интервала (шага решётки) и следующей формулы: “ = A3 + 0,002 ”.
Как видно, эта формула является рекуррентной, т. е. зависит от предыдущего значения и если
скопировать ячейку A4, а затем начать вставлять её содержание в нижележащие A5, A6, A7, и
так далее, то в них автоматически будут возникать корректные значения: 0,004, 0,006, 0,008,
так как в Excel, как и в других совместимых редакторах электронных таблиц, все формулы по
умолчанию считаются рекуррентными и все ссылки на ячейки по умолчанию относительные,
а не абсолютные. Другими словами, если значение в ячейке рассчитывается как, например,
сумма двух чисел из соседних ячеек, одной сверху и другой справа, то копирование формулы
в новое место приведёт к автоматической перенастройке этих ссылок так, чтобы указывать
на ячейки сверху и справа, но относительно уже новой ячейки. Такая авто-настройка ссылок
упрощает копирование формул на новое место, однако, если необходимо вписать формулу в
тысячи ячеек вплоть до позиции A5002, то этого упрощения недостаточно и в ручном режиме
это проделать сложно. Для таких случаев предназначен маркер заполнения, реализованный во
всех современных редакторах таблиц – маркер находится в правом нижнем углу выделенной
ячейки, за него можно ухватить мышью, потянув в любом направлении (вправо, вниз, влево
или вверх), при этом формула из стартовой ячейки будет автоматически копироваться во все
встреченные позиции. Наконец, в некоторых редакторах предусмотрена ещё большая степень
автоматизации, когда копирование ячейки направлено строго вниз – в этом случае достаточно
осуществить двойной щелчок мышью по маркеру заполнения, что приведёт к копированию
во все нижние ячейки вплоть до нижней границы таблицы (т. е. до позиции A5002).
Теперь в столбцах A и B находятся соответственно моменты времени и величина напряжения,
зарегистрированная на отведении I в эти моменты, а значит теперь легко вывести ЭКГ в виде
графика путём выделения обоих столбцов и выбора в пункте меню «Вставка» подходящего
типа графика, т. е. опции «Точечная с прямыми отрезками» из выпадающего меню диаграмм.
Очевидно, построенный график идентичен фрагменту ЭКГ, наблюдаемому в веб-приложении
LightWAVE, а подобрав стиль диаграммы можно добиться и внешнего сходства (см. рис ??).
Как и предполагалось, на рисунке ?? видны легкоразличимые характерные паттерны сигнала,
оставляющие на ЭКГ почти регулярные остроконечные пики – расстояние между ними есть
искомые RR-интервалы, из которых и следует построить КИГ (кардиоинтервалограмму). Для
начала возможно локализовать пики вручную, наподобие того, как это было проделано ранее
исследователями из данной группы [??]. Вообще, кардиологи отмечают на ЭКГ не одни лишь
пики, но целый ряд различных явлений, имеющих значение для специалистов и отмечаемых
особыми символами (кодами) [??], но сейчас интерес представляют только пиковые значения
нормальных ударов (англ. normal beat), отмечаемые буквой “N”, как это приведено в разделе
Annotations [??], где можно видеть, что для отведения I (Annotator: i) первые удары отмечены
на 1,328 и на 2,688 секунде, что даёт значение в 1,360 секунду для всего NN-интервала (этот
термин часто используется в данном контексте как синоним к RR-интервалу).
Разумеется, в век растущих объёмов информации никак не удастся осилить задачу получения
полной аннотации для всех оцифрованных ЭКГ-сигналов исключительно в ручном режиме, в
связи с чем исследователями разработаны различные методы автоматического аннотирования
ЭКГ [??]. Однако, несмотря на значительное облегчение труда специалистов, автоматическая
обработка иногда допускает собственные ошибки в описании сигналов, что требует введения
дополнительной ручной перепроверки (верификации) результатов. Такая полуавтоматическая
(англ. semiautomatic) обработка сигналов даёт наиболее качественные и всё ещё оперативные
результаты, охватывая гораздо большие объёмы данных, чем это возможно было бы сделать в
ручном режиме, однако сильно уступая и по скорости, и по объёмам полной автоматизации
процессов анализа. Для большего понимания, типичные ошибки автоматической обработки
продемонстрированы ниже на конкретном примере, т. е. на текущем фрагменте ЭКГ-сигнала.
Автоматический рассчёт R-R интервалов
Итак, на Листе 2 в столбцах A и B находятся время в секундах и напряжение в милливольтах,
зарегистрированное на отведении I в данные моменты времени. Требуется последовательно
вывести значения интервалов времени между пиками соседних паттернов. Эту задачу будет
логичным разбить на три этапа:
1) выделение пиков;
2) поиск позиции пиков;
3) рассчёт R-R интервалов.
Тогда для поиска пиков можно предложить метод поиска экстремумов, т. е. точек, в которых
производная сигнала меняет свой знак. Применение формул численного дифференцирования
в электронных таблицах не вызовет трудностей, однако такой подход всё равно неприменим,
т. к. таким образом выделятся не только глобальные максимумы паттернов (пики), но и масса
промежуточных локальных экстремумов. Существует способ отсечения побочных «пичков»,
когда используется пороговое значение – величина, ниже которой измерения сигнала следует
игнорировать, обнулять. Такой способ часто применяется в различных приложениях [??], т. к.
он сильно упрощает анализ «значимой» части сигналов, однако следует помнить, что выбор
оптимальных пороговых значений является отдельной нетривиальной задачей, ведь слишком
высокие значения порога отсекут наименьшие из искомых пиков, а вот неоправданно низкие
подмешают в выдачу ряд ложных промежуточных пиков. Пока же пороговое значение можно
выбрать вручную, на основании визуальной оценки текущего графика (рис. ??). Считая порог,
например, равным 0,6, можно уверенно отделить окрестности искомых пиков от остальной
части сигнала. Далее можно вывести все требуемые надпороговые значения в столбец C, так
его и озаглавив (т. е. вписав в ячейки C1/C2 слова «Надпороговые»/«значения»), после чего
останется ввести в ячейку C3 формулу “=ЕСЛИ (B3>0,6; B3; 0)” и распространить её на все
низлежащие ячейки столбца.
Теперь с высокой степенью уверенности для каждой окрестности можно утверждать, что её
глобальный максимум совпадает с пиком текущего паттерна и что паузы между максимумами
равны искомым RR-интервалам. Но как найти глобальный максимум для каждой окрестности
надпороговых значений, если их протяжённость, как и дистанция между ними, варьируется?
Очевидно, что в таком случае любая точка с неотрицательным надпороговым значением
может оказаться одной из искомых точек максимума, а значит для всех позиций потребуется
провести проверку: является ли значение в этой позиции наибольшим для всего окружения
точки в некоторого радиусе r. Иными словами, например, если r = 5, для всех точек следует
проверить, является ли значение в данной позиции больше пяти значений до этой позиции и
пяти значений после неё. Таким образом из целого ряда значений на каждом шаге выделяется
небольшое «окно» из (2r+1) точек, которое «скользит» вдоль координатной оси, смещаясь на
каждом шаге на одну позицию – такой подход к обработке сигналов и данных в самом общем
случае называется методом скользящего окна [??], а в рассмативаемом случае – максимумом
скользящего окна или скользящим максимумом [??].
Реализация метода скользящего окна в электронных таблицах отвечает базовым принципам
работы в этой среде, так как все формулы над ячейками, как говорилось ранее, по умолчанию
считаются рекуррентными. Дополнительным преимуществом в подобных средах является то,
что большинство встроенных функций предполагает расширение их действия на фрагменты
таблиц, как то: вертикальные или горизонтальные диапазоны столбецов или строк, или даже
прямоугольные блоки из соседних табличных значений. Например, если в ячейку D6 ввести
формулу “=MAX (1; 2)”, то в ней возникнет число “2”, а если “=MAX (1; 2; 3)”, то число “3”,
но данная функция предполагает, что в качестве входных параметров могут выступать также
названия ячеек, таким образом замена фомулы на “=MAX (A3;A4;A5)” приведёт к появлению
в D6 максимального из значений, расположенных в ячейках A3,A4 и A5. Следует помнить,
что для удобства пользователей предусмотрен более краткий способ ввода диапазона ячеек,
когда они расположены последовательно – в этом случае указываются только крайние ячейки
блока ячеек, т. е. самая верхняя/левая и самая нижняя/правая (N.B.: разделённые
двоеточием), что в данном случае означает ввод: “=MAX (A3:A5)”. Получается, что легко и
просто можно задать диапазон произвольной длины, в том числе, охватив окно из r ячеек
надпороговых значений до текущей позиции и столько же после неё, то есть “=MAX
(С1:С11)” в случае r = 5 на точке D6. Скольжению окна из 11 ячеек соответствует
автоматическое копирование формулы на все низлежащие ячейки столбца до конца таблицы,
после чего можно озаглавить столбец, вписав в ячейки D1/D2 строки
«Скользящий»/«максимум», а недостающие верхние ячейки заполнив нулями (D3, D4, D5).
Примечание: отметим особо, что диапазон ячеек таблицы, определяемый через двоеточие, не
должен быть строго вертикальной колонкой или фрагментом горизонтальной строки, а может
быть некоторой прямоугольной областью таблицы. Например, выражение “=СУММ(A1:D3)”
задаёт прямоугольную область (блок) из двенадцати ячеек (по четыре в ряд) и суммирует все
числовые значения, оказавшиеся внутри рамки, ограниченной столбцами A,D и строками 1,
3. Вообще, поблочный анализ популярен в электронных таблицах, позволяя элегантно и
просто реализовать в подобных средах ряд довольно сложных задач, от бухгалтерских
рассчётов до оконных преобразований и фильтров данных.
Примечание: очевидно, если скопировать ячейку с формулой в новое место, то и рамка блока
автоматически сместится на столько же строк и столбцов вслед за переносом. Но что делать,
если потребуется иной вид смещения рамки, когда ей можно скользить по горизонтали, но не
«съезжать» на другие строки? В этих случаях следует закрепить строки знаком доллара ($),
вставив перед индексами строк. Тогда формула выше примет вид: “=СУММ (A$1:D$3)”. Так
же можно закрепить столбцы, указав знак доллара перед названиями: “=СУММ ($A1:$D3)”.
Наконец, чтобы зафиксировать весь диапазон, не позволяя блоку смещаться ни по вертикали,
но по горизонтали, следует записывать: “=СУММ ($A$1:$D$3)”.
Примечание: здесь же интересно было бы также отметить, что в большинстве электронных
таблиц существует возможность явного смещения блока с помощью специальной встроенной
(базовой) функции. Так, формула: “=СУММ (СМЕЩ (A100:B200; -1; 2))” использует сдвиг
блока A100:B200 на 1 строку вверх, 2 столбца вправо и эквивалентна “=СУММ (C99:D199)”.
Таблица готова к завершению первого этапа – к нахождению моментов времени с пиковыми
значениями. Легко видеть, что существуют строки, в которых Надпороговые значения равны
Скользящему максимуму в данной позиции – это и есть искомые пиковые моменты, согласно
введённому ранее определению. Для выделения таких моментов времени следует ввести ещё
одну колонку таблицы, вписав в E1/E2 название столбца: «Пиковые»/«моменты», а в ячейку
E3 формулу “=ЕСЛИ (И (C3=D3;D3<>0);A3;"")”, которую затем следует скопировать во всю
длину таблицы. Как видно, большинство ячеек столбца остались пустыми, но некоторые из
них: E15, E668, …, заполнены искомыми отсчётами времени, что рассчитывалось по формуле
так: «ЕСЛИ текущее пороговое значение РАВНО текущему скользящему максимуму И оно НЕ
РАВНО нулю, то в ячейку записывается текущий отсчёт времени, иначе же – пустая строка».
Второй этап поставленной выше задачи заключается в расчёте промежутков времени между
пиками, что можно проделать вручную, выбрав непустые ячейки колонки Пиковые моменты.
Ручная работа упрощается, если эту колонку скопировать на новый лист без форматирования
(Ctrl+Shft+V), воспользовавшись далее меню: «Данные → Сортировка по возрастанию». Но
так как процесс должен быть полностью автоматизирован, такой подход не годится. Вообще,
задача автоматической фильтрации «пустых ячеек» для большинства алголоподобных языков
программирования является тривиальной, однако в большинстве ПО для электронных таблиц
автоматическая фильтрация реализована так, что применение подобного инструмента требует
изучения новых навыков, имеющих специфику в каждой среде, а значит «инструментальное»
решение фильтра не будет легко переносимо на различные среды и даже на новые таблицы.
Ввиду вышесказанного предпочтительнее строить решение, используя лишь базовые фунции.
Простейшим началом станет рассчёт по формуле “= МИН (E1:E5002)”, результат чего равен
минимальному, т. е. первому значению времени из Пиковых моментов. При этом нечисловые
значения, включая пустые клетки, будут проигнорированы. Далее следует ввести в F1/F2
строки «Поиск»/«пиков», а эту начальную формулу в F3, и задуматься над тем, как отыскать
второй, третий и все следующие моменты времени, записав их последовательно под первым
из искомых отсчётов, уже полученным в F3. Видно, что первое значение взято из 15 строки, а
значит, сместив диапазон на 15 клеток и записав в F4: “= МИН (СМЕЩ (E1:E5002; 15; 0))”,
удасться найти второй момент времени пропустив первый. Очевидно, что так же можно легко
найти третий, четвёртый и другие моменты, если знать позицию предыдущего отсчёта, но
тогда придётся вручную переписывать формулу, задавая очередные смещения в явном виде.
Для автоматизации поиска моментов потребуются вспомогательные построения, под которые
можно выделить столбец G, вписав в G1/G2 строки «Позиции»/«моментов», а в G3 вставив:
“=ПОИСКПОЗ (F3;E$1:E$5002)”, построив формулу на одной из самых основных функций.
Причём рамка этого диапазона жёстко привязана к строкам, не позволяя ей «соскальзывать»
при переносе формулы на низлежащие ячейки: G4, G5 и др. Но прежде следует переписать
формулу из F4, теперь указывая смещение в неявном виде по ссылке на момент времени, уже
найденный в G3: “= МИН (СМЕЩ (E$1:E$5002; G3; 0))”, где рамка также зафиксирована. И
так получено рекуррентное соотношение, согласно которому значение в F4 зависит от G3, а
G3 зависит от F3, что в итоге задаёт ряд: F3 → G3 → F4 → G4 → F5 → … , который следует
продолжить до конца таблицы (например, сначала щёлкнув по маркеру заполнения в ячейке
F4, а затем уже в G3).
Третий этап заключается в рассчёте RR-интервалов, которые естественно было бы поместить
в стобец H, озаглавив его строками «Интервалы»/«R-R» в ячейках H1/H2. Очевидно, что если
вписать в H3 разность “=F4-F3” и распространить эту формулу вниз, то в первых же ячейках
получится выделить искомые R-R интервалы. Однако большая часть колонки будет заполнена
ошибочными значениями “#Н/Д” (т. е. «Нет Данных»), т. к. данные о последующих пиковых
моментах действительно отсутствуют. Несмотря на то, что поставленная выше задача уже, по
сути, выполнена, наличие ошибок в итоговой колонке таблицы крайне нежелательно, т. к. эта
колонка может быть использована и для дальнейшего анализа данных, приводя к ошибочным
либо невозможным результатам. Например, для того, чтобы узнать среднее значение для R-R
интервалов по всей колонке следует воспользоваться формулой “= СРЗНАЧ (H1:H5002)”, но
сейчас такой анализ приведёт к ошибкам, избежать которые можно, если заранее освободить
столбец H от всех “#Н/Д” значений. Для этого впишем в H3 более сложную, но корректную
формулу: “= ЕСЛИ (И (ЕНД (G3); ЕНД (G4)); ""; F4-F3)”, где уже проводится проверка: Не
находятся ли ошибки вида “#Н/Д” в ячейках с индексами строк, в которых обнаружены пики
сигнала? Теперь скопировав формулу из H3 до конца таблицы, легко видеть: все искомые R-R
интервалы получены без ошибок, а формула среднего значения выдаёт корректный результат.
Примечание: внимательному читателю может показаться, что откорректированную формулу
из H3 можно значительно упростить, ограничившись одной лишь проверкой для ячейки G4,
но тогда он, читатель, может упустить ошибку, которая произойдёт в самой последней ячейке
этой колонки, H5002, что является частой ошибкой у неопытных пользователей электронных
таблиц. Вообще, после любого изменения части таблицы считается правилом хорошего тона
проверять не нарушило ли оно целостности таблицы и не внесло ли оно ошибки в ключевых
колонках и столбцах, что особенно важно при командной работе над общим проектом.
Примечание: внимательному читателю могло показаться, что если бы рекуррентная формула
из F4 была переписана: “= МИН (СМЕЩ (E$1:E$5002; ПОИСКПОЗ (F3;E$1:E$5002); 0))”,
то можно было отказаться от вспомогательных построений в G столбце, и это действительно
так, но такой подход даёт дополнительные возможности, смысл которых будет раскрыт ниже.
Верификация и уточнение данных
Теперь будет полезным вспомнить про раздел Annotations – выше ранее по описанию удалось
вручную рассчитать первый N-N интервал, равный 1,360 секундам и лежащий между 1,328 и
2,688 секундами, что согласно описанию на сайте соответствует 664 и 1344 отсчёту времени
(англ. sample) с интервалом выборки 0,002 секунды. Далее было бы правильным сопоставить
результаты, получаемые вручную на сайте, и результаты на Листе 2 электронной таблицы.
Во-первых, можно заметить, что первый пик ЭКГ в описании на сайте проигнорирован, но на
Листе 2 он отмечен и это привело к появлению дополнительного (первого) R-R интервала. С
остальными интервалами, начиная с интервала в 1,360 секунд, результаты точно совпадают.
Во-вторых, несмотря на дальнейшее совпадение N-N интервалов на сайте и R-R интервалов
на Листе 2, легко видеть, что позиции пиковых значений численно разнятся. Так, в описании
ряд начинается с чисел: 664, 1344, 2002, но в таблице отмечены: 668, 1348, 2006. Индексы на
Листе 2 как будто бы сдвинуты на четыре позиции. Интересно, что этот сдвиг вызван сразу
тремя совершенно различными причинами. Первая из них – сдвиг на 2 позиции, заключается,
конечно же, в том, что в столбцы вставлены названия колонок, заняв две строки из диапазона.
Вторая причина – в электронных таблицых принято натуральное индексирование, т. е. отсчёт
объёктов начинается с единицы (как квартиры в доме и дома на улице), но вот в большинстве
языков программирования принята так называемая нумерация с нуля, что снижает индексы на
сайте ещё на одну позицию. Третья причина вызвана систематической ошибкой в описании
на сайте, а именно сдвигом пикового момента ровно на один отсчёт раньше по времени. Это
легко видеть и по таблице на сайте, и по электронной таблице, если взять, к примеру, первый
пик сигнала из описания – 1,328, то легко видеть, что следующее значение, на 1,330 секунде,
выше. Точно так второй пик из описания должен быть не на 2,688, а на 2,690 секунде, и т. д.
В процессе верификации (сверки) легко придти к общему выводу – ритмограммы в таблицах,
т. е. RR интервалы, вычислены корректно. Однако корректность вычислений условна, т. к. она
основана на предположении, что все пиковые значения сигнала попадают чётко в дискретные
моменты времени, когда величина сигнала фиксируется. На самом деле это не так, чаще всего
фиксируется не сам пик, а соседние состояния, попавшие на дискретные моменты, и по ним
можно приблизительно определить тот момент времени, на который пришёлся пик сигнала.
Вопрос о том, насколько важно снижать погрешность определения пиков ЭКГ при получении
ритмограмм до сих пор остаётся открытым, вызывая дискуссии среди специалистов [??, ??],
однако все основные подходы повышения точности отыскания пиков можно разделить на две
группы:
1) технические;
2) аналитические.
Все технические подходы зависят исключительно от аппаратных возможностей и обычно они
состоят в повышении частоты дискретизации [?] и глубины квантования [?] сигналов. Так, за
историю своего развития частота повысилась от пары десятков отсчётов в секунду до тысячи
герц, а разрядность квантования выросла от 8 бит до нескольких байтов на один отсчёт ЭКГ.
Не совсем ясно, насколько это оправданно с точки зрения получения качественных КИГ и не
является ли такое повышение объёмов ЭКГ-данных избыточным. Хотя известна масса других
областей медицины, где необходимость повышения разрешения и разрядности сигналов не
вызывает никаких сомнений. Например, разрядность цифрового рентгеноснимка начинается
с 10 битов на точку изображения, что уже требует в четыре раза больше оттенков серого, чем
способен вывести на экран обычный дисплей – но меньшая глубина квантования не имела бы
смысле для ренгенолога [??]. С другой стороны, повышение частоты дискретизации сигнала
не способно решить все вопросы, связанные с определением действительного пика, особенно
когда это критически важно, например, в задачах, связанных с масс-спектрометрией [??], так
что всё равно приходится прибегать к «искусственному» повышению разрешения сигнала – к
аналитическим подходам.
Действие простейщего аналитического подхода легко продемонстрировать на трёх примерах,
представленных на рисунке ??. Действительно, пусть известны только значение локального
максимума и значения в двух соседних точках, слева и справа от него – тогда логичным будет
выделить три характерных случая: 1) соседние значения равны между собой; 2) левое выше;
3) правое выше. В первом из описанных случаев (при отсутствии любой другой информации)
следовало бы полагать, что действительный пик полностью совпадает с зарегистрированным
локальным максимумом. Но такие случаи на практике крайне редки – обычно предполагают,
что действительный пик сигнала смещён относительно центрального значения, причём влево
во втором случае, а в третьем вправо. Более того, чем больше разница между левой и правой
величинами, тем сильнее смещение от центра. Но как же это смещение рассчитать численно?
Интуитивно ясно, что если через три эти точки можно было провести некую гладкую линию,
то верхушка этой кривой прошла бы близко от искомого действительного максимума сигнала
из этой окрестности. Процесс «достраивания» дискретного сигнала в промежутках между его
известными значениями называется интерполированием и сам является предметом многих
научных исследований, но здесь можно ограничиться самыми базовыми понятиями из этой
теории – формулой Лагранжа.
В предельном случае, если дискретный сигнал состоит всего из двух известных величин: y0 и
y1, зафиксированных в моменты x0 и x1, то они, по сути, определяют две точки на плоскости,
через которые кривая сигнала точно проходит. За неимением дополнительной информации в
этом случае останется лишь соединить эти две точки отрезком, «достроив» так недостающие
значения сигнала на промежутке между x0 и x1. Полученный отрезок есть часть некоторой
прямой, значит в общем виде точки отрезка заданы уравнением: y=kx+b, где k – коэффициент
наклона линии, а b – базовое значение в точке x=0. Для определения параметров прямой, как
известно из школьного курса алгебры, следует решить систему из двух уравнений, например,
с помощью метода подстановок:
Заметим, что в предельном случае: точек сигнала две, параметров кривой – два, уравнений
системы – тоже два. Такое совпадение неслучайно и оно сохранится для случая из трёх точек
сигнала, или четырёх, пяти и так далее. В общем случае справедливо утверждение [??]: через
любые N точек дискретного сигнала можно провести один и только один интерполяционный
многочлен, состоящий ровно из N членов (т. е. от 0-ой до (N-1)-ой степени), что часто удобно
представлять в канонической форме:
При решении задач информатики часто возникает необходимость в переход от одной системы
описания данных к другой, причём нередк так или иначе формулируется принцип сохранения
независимых переменных. Как для систем физического мира действуют законы сохранения
массы/энергии/импульса, в информатике можно было бы тоже сформулировать общий закон
сохранения независимости: в изолированной информационной среде при переходе от одной
системы описания данных к другой количество независимых параметров остаётся прежним
либо уменьшается. В некотором смысле этот закон напоминает второе начало термодинамики
(закон возрастания энтропии), что полезно запомнить как мнемоническое правило, которое
пригодится в последующем изложении материала.
Теперь же ясно, что через каждую тройку значений сигнала (y0, y1, y2) можно единственным
образом пропустить параболу, определяемую тремя параметрами, например, как (a0, a1, a2)
канонической формы, но для этого придётся решить систему из трёх уравнений. Как в случае
с системой двух уравнений, можно воспользоваться методом последовательных подстановок
и в случае трёх, как и для любой другой системы произвольного размера. Причём для СЛАУ
(системы линейных алгебраических уравнений) правильнее будет называть подобный способ
решения методом Гаусса [??]. Несмотря на очевидную простоту этого метода, с повышением
размерности системы все вычисления довольно быстро становятся невозможными для счёта
вручную, а с некоторого порога слишком долгими даже для современных ЭВМ. Насколько же
долгими? Настолько, что решение тестовых СЛАУ на время нередко используется для оценки
быстродействия мощных вычислительных кластеров [??] и математических программ [??].
Ввиду большей сложности расчёта на трёх точках, следует отказаться от решения системы из
трёх уравнений в пользу прощеполучаемого интерполяционного многочлена второго порядка
(т. е. параболы), пускай даже выраженного не в канонической форме. Главное, что благодаря
канонической форме точно известно, что искать следует многочлен второй степени,который в
точности и однозначным образом пройдёт через любые три предоставленные точки сигнала.
На помощь в такой ситуации приходит интерполяционный многочлен Лагранжа – изящный и
элегантный способ представления интерполяционного многочлена, не требующий никаких
предварительных вычислений. Это блестящее инженерное решение, но выполняющее строго
свою функцию и малопригодное, в отличии от канонической формы, для проведения над ним
дальнейших аналитических преобразований.
Изложение метода Лагранжа целесообразно начать также с предельного случая, когда заданы
только две точки дискретного сигнала, как рассматривалось выше. Для начала упростим ещё
и решётку дискретных значений, положив: x1=0, x2=1, x3=2 и т. д. Тогда, минуя вычисления,
интерполирующую линию можно задать в виде:
y = y1 * (1-x) + y2 * x.
Легко видеть, что при x = 0 второе слагаемое уничтожается, а сомножитель для y1 становится
равным единице – так легко и просто получается требуемый «проход» через первую точку. С
другой стороны, при x = 1 аналогичные рассчёты происходят на втором отсчёте, обеспечивая
точный «проход» линии и через вторую точку. Между же означенными точками происходит
плавный «переход» линии от одного значения к другому согласно указанной формуле. Теперь
можно вернуться к случаю произвольных отсчётов решётки (x1, x2, …), который отличается
от первого только переносом начала координат и коэффициентами масштабирования:
y = y1 * (x-x2)/(x1-x2) + y2 * (x-x1)/(x2-x1).
Но если такой метод применим для двух точек, что мешает перенести его точно также и на
случай трёх, четырёх и более точек? Действительно, тогда для случая трёх точек получим
а в общем случае:
где M – количество точек, через которые проходит данный интерполирующий многочлен.
Отметим, многочлен Лагранжа не случайно имеет такую же степень, что интерполяционный
многочлен в канонической форме – это одна и та же кривая, но представленная в разных
формах, и иначе не могло быть, вследствие требований о существовании и единственности
решения для системы независимых линейных уравнений [??]. Но как было сказано выше,
метод Лагранжа проще, не требует проведения предварительных рассчётов, вычисления
дискриминантов или чего-либо другого.
Следует вспомнить, какая проверка использовалась для отыскания локального максимума в
дискретном случае – значение должно быть выше прилегающих соседних значений. Но при
этом диапазон ошибок составит ±h/2, где h – шаг решётки [??], что для исследуемого набора
составит ±10 миллисекунд. Предполагая, что этой точности недостаточно, но получив
теперь в аналитическом виде представление интерполирующей кривой, проходящей через
соседние точки «дискретного» максимума, можно отыскать «действительный» максимум
сигнала, если знать и производную данной кривой. Связь производной с точками экстремума
функции (т. е. точек локального максимума или минимума) также входит в курс школьной
алгебры [??], но напомним, что в точках экстремумов производная функции всегда меняет
свой знак, причём если знак меняется с отрицательного на положительный – в этой точке
находится локальный минимум, а если наоборот – максимум. Ранее предполагалось, что
интерполирующая кривая должна быть гладкой, что в математическом анализе подразумевает
соблюдение конкретного свойства – кривая должна быть описана непрерывно
дифференцируемой функцией [??]. Что это даёт? Если производная непрерывна, то переходя,
например, от отрицательных значений к положительным, она непременно пройдёт через
точку, в которой она равна нулю – значит поиск экстремумов можно значительно упростить,
заменив его на простое правило: искать нули производной и проверять, сменяется ли знак
производной при переходе через эти точки.
Если интерполирующая кривая представлена многочленом, такое правило всегда применимо,
т. к. все многочлены обладают бесконечным порядком гладкости, т. е. производные любого
порядка являются непрерывными функциями. Тогда задачу можно упростить до поиска
нулей производной, а в случае с параболой – это всего одна точка. Ясно, что если бы кривая
была представлена в канонической форме, то её символьное дифференцирование оказалось
бы совершенно тривиальной задачей, но и над формулой Лагранжа на трёх точках несложно
проделать такие преобразования.
Но прежде упростим формулу, проделав подстановку переменной: t=(x–x2)/h, перенося точки
решётки с позиций (x1, x2, x3) на отцентрированные точки (-1, 0,+1). Тогда получим:
где f(t) = y(x), а f_,f0, f^ равны значениям y1, y2, y3 соответственно. Упростив запись и сделав
приведение слагаемых можно получить:
Полученное выражение есть интерполирующая кривая Лагранжа третьей степени (парабола),
записанная теперь в канонической форме.
Примечание: интересно, что выражение в знаменателе первого слагаемого совпадает со 2-ой
производной при численном дифференцировании функции на регулярной решётке с шагом
единица, а сомножитель второго слагаемого совпадает с конечной разностью для вычисления
первой производной с высокой точностью [?]. Но тогда выражение можно переписать в виде:
что фактически является степенным рядом, аппроксимирующим функцию в точке t = 0, т. е.
рядом Тейлора (точнее Маклорена [??]). Таким образом получается, что и интерполирующий
многочлен Лагранжа, и каноническая форма, и ряд Тейлора из трёх первых слагаемых – суть
одна и та же парабола, выраженная в трёх разных видах. Так происходит часто, но не всегда,
т. к. существует разница между интерполирующими и аппроксимирующими кривыми [??].
Теперь применим полученную форму для нахождения производной аналитическом виде для
Автоматический рассчёт порогового значения
Наконец, можно приступить к анализу полученной КИГ, рассчитав по нему например среднее
ЧСС пациента. Найденных R-R интервалов не так много, но даже одного из них достаточно
для рассчёта мгновенного ЧСС, как это показано выше. Значит колонке из интервалов можно
сопоставить колонку из мгновенных ЧСС, вписав строки «Мгновенные»/«ЧСС» в I1/I2, затем
формулу “= ЕСЛИ (H3="";""; 60/H3 )” вписав в ячейку I3 и растянув её до конца таблицы.
Полученных значений уже хватит для того чтобы приблизительно оценить частоту сердечных
сокращений пациента в момент регистрации – для этого в ячейку J3 можно вписать простую
формулу: “= СРЗНАЧ (I1:I5002)” и надписав в J1/J2 название «Средняя»/«ЧСС» (рис. ??).
Рассчётный пульс (т. е. ЧСС), полученный по первым 10 секундам ЭКГ из набора data/1 [??],
как видно, окажется равным почти 45 ударам в минуту, а для среднестатистического человека
это довольно низкий показатель. Здесь будет полезно вспомнить, что в разделе Summary есть
подраздел Notes (англ. пометки), в котором можно видеть краткий анамнез пациента, взятый
из специального файла-заголовка. Как видно из анамнеза (см. рис. ?), тестовые исследования
на Листе 2 проводились на ЭКГ женщины 51 года, страдающей от синусовой брадикардии,
что объясняет и всецело согласуется с наблюдаемым пульсом, рассчитанным в ячейке J3.
WFDB Annotation Codes
https://physionet.org/physiotools/wpg/wpg_32.htm
К сожалению, названия функций в переводе на русский не отличаются особой
благозвучностью, но возможно, отчасти благодаря именно этому такие сокращений легче
запоминаются.
на примере которой ниже продемонстрирован процесс получения ритмограмм из ЭКГ,
Verified
Ноли сумм ЭДС не случайны …
В качестве рабочих материалов для данного методического пособия имеет смысл выбирать
общедоступные данные, например, через сеть Интернет. Одной из самых ранних и известных
коллекций материалов такого рода являются данные, полученные в институте в результате
двухчасового наблюдения
Медицинская диагностика заболеваний
/Interbeat_interval
Без интернета
В качестве иллюстрации можно привести старинный анекдот о двух случайных попутчиках,
которые решили сыграть в карты, изображая абсолютных профанов, однако один из них сразу
же заметил, как только он распаковал новую пачку, что одна из карт в колоде отсутствует, что
тут же подтвердил другой, также взвесив колоду в руках: «Точно, здесь нет валета пик». Но
несмотря на анекдотичность ситуации, следует согласиться с тем, что если бы взвешивание
осуществлялось с точностью аптекарских весов, т. е. до долей грамма, то отсутствие карты не
так сложно обнаружить. Более того, выяснить, какой именно карты не достаёт в колоде, тоже
несложно путём её взвешивания, учитывая специфичное количество краски на каждой карте,
однако и точность измерения должна быть куда выше, до долей миллиграмма, как, например,
у лабораторных весов.
Бернулли
округления
var view = new DataView (R.result, bOFFSET);
https://archive.physionet.org/faq.shtml#file_types
10 heartbeat time series in this directory: 5 young subjects
(denoted as Y1.txt, Y2.txt, etc) and 5 elderly subjects (O1.txt,
O2.txt, etc).
Each file contains 1 column data of interbeat interval (in second).
The length of the recording is approximately 2 hours for each subject.
For detailed description of the database, see
Iyengar N, Peng C-K, Morin R, Goldberger AL, Lipsitz LA.
Age-related alterations in the fractal scaling of cardiac
interbeat interval dynamics. Am J Physiol 1996;271:1078-1084.
These 10 data sets form a sub-set of the complete database studied in
the above article.
PLEASE NOTE: THIS COLLECTION OF HUMAN HEART RATE AND GAIT DATABASES
WAS CONSTRUCTED AS A TEACHING RESOURCE FOR THE NECSI INTENSIVE COURSE
(OCTOBER 1999): "THE MODERN SCIENCE OF HUMAN AGING"
(www.necsi.org). AS SUCH, THIS SPECIFIC "MINI-COLLECTION" IS NOT
INTENDED FOR BASIC RESEARCH/PUBLICATIONS. HOWEVER, IT MAY BE USEFUL IN
OTHER CLASSROOM OR TUTORIAL SETTINGS, AND FOR SELF-GUIDED EXPLORATIONS
INTO THE WORLD OF BIOLOGIC COMPLEXITY. FOR CURRENTLY AVAILABLE
RESEARCH DATABASES, PLEASE CONSULT THE WEBSITE OF THE RESEARCH
RESOURCE FOR COMPLEX PHYSIOLOGIC SIGNALS (www.physionet.org).
<html>
<body>
<textarea id="out" rows="25"> ... </textarea><br>
<input type="file" onchange="R.readAsArrayBuffer(this.files[0])">
<script>
var A = 0, B = 1000, N=2, T = Uint16Array;
var R = new FileReader(), S = 'Extracted data:';
R.onload = function () {
var bin = new T ( R.result.slice ( A, B - A ));
for (var i in bin) S += (i%N?'\t':'\n')+bin[i];
document.getElementById ("out").value = S;
}
</script>
</body>
</html>