збіжність

1
1 . Дослідження збіжності
1.1. Основні означення, необхідна умова збіжності ряду
Нехай задана послідовність дійсних чисел ( xn ) . Числовим рядом
 xn
 n 
називається послідовність дійсних чисел   xk  .
 k 1 
n
Числа xn та S n   xk називаються відповідно n  м членом (загальним
k 1
членом) та n  частковою сумою ряду.
Границя послідовності часткових сум ряду, якщо вона існує і скінчена,
називається сумою ряду
 xn та позначається символом

 x k . Ряд, що має суму,
k 1
називається збіжним. Не збіжний ряд називається розбіжним.
Як ми бачимо, на відміну від теорії послідовностей, послідовність часткових
сум може збігатися до нескінченності (тобто в наших визначеннях з теорії
послідовностей бути збіжною), але відповідний числовий ряд вважається
розбіжним. Дуже рідко, в особистих випадках, про такий ряд можемо сказати, що
він збігається до нескінченності.
З означення ряду слідує, що будь-яка послідовність дійсних чисел ( S n ) може
розглядатися як деякий ряд, членами якого є числа x n  S n  S n 1 n  N S 0  0  .
Теоре
(Необхідна умова збіжності ряду)
ма 1.
Якщо ряд
 xn
збігається, то послідовність його загальних
членів прямує до нуля.
Доведення. Якщо
 xn - збіжний, то послідовність його часткових сум має
границю, позначимо її як S . Але тоді x n  S n  S n 1  S  S  0 .
2
Теорема доведена.
(Критерій Коші)
Теоре
ма 2.
Ряд
 xn
збігається тоді і тільки тоді, коли   0 N ( ) :
n  N ( ) p  N
n p
 xk
.
k  n 1
Доведення теореми безпосередньо слідує із застосування критерію Коші для
послідовності часткових сум ( S n ) .
Вже тут можна побачити, що багато тверджень можна формулювати як в
термінах теорії послідовностей так і в термінах теорії рядів. Один з прикладів вже
наведений вище – це критерій Коші. Наведемо невелику таблицю, в якій терміни,
що відповідають один одному в цих теоріях, наведені в одному рядку.
Теорія рядів
Теорія послідовностей
Ряд
Послідовність
Член ряду
Різниця між членами послідовності
Часткова сума ряду
Член послідовності
Сума ряду
Границя послідовності
Збіжний ряд
Збіжна послідовність
Згрупований ряд
Підпослідовність
Сума згрупованого ряду
Часткова границя послідовності
Ряд, що задовольняє умову Коші
Фундаментальна послідовність
Ряд, що має обмежені часткові
Обмежена послідовність
Ряд з невід’ємними (додатними)
Неспадна
суми
членами
(зростаюча)
послідовність
Цю таблицю далі можна буде розширити, при поглибленні вивчення теорії
рядів. Крім того її можна продовжувати далі штучним чином. Вільний перехід з
3
однієї мови на іншу в деяких випадках може повністю або частково
спростити доведення тієї чи іншої теореми.
Однак цілком зрозуміло, що є твердження, які природніше формулювати в
термінах лише однієї мови, або навіть вони зовсім не формулюються в термінах
іншої мови. Одним з прикладів такого твердження є теорема Рімана, з якою ми
познайомимось пізніше. Будуть також твердження, що формулюються на мішаній
мові, тобто з використанням термінології теорії рядів та теорії послідовностей,
наприклад, теореми Абеля та Діріхле.
 n j 
Ряд   x k 
називається n  залишком ряду
 k  n 1  jN
 xn .
(Про n  залишок числового ряду)
Нас
лідок.
Ряд
 xn
збігається
чи
розбігається
одночасно
з
своїм
n  залишком. Якщо ряд збігається, то його n  залишок збігається до
нуля.
Доведення. Якщо ряд
 xn збіжний і його сума S , тоді
S n  S  rn , де
послідовність (rn ) як раз і є n  залишком цього ряду. З відомої теореми з теорії
послідовностей слідує, що S n  S   rn  0 . Аналогічно розглядається випадок
розбіжного ряду.
Наслідок доведено.
Із зв’язку рядів та послідовностей легко доводиться наступна теорема.
Теоре
(Лінійність збіжних рядів)
ма 3.
Нехай ряди
 ( x n  
 xn та  y n збігаються,  ,   R , тоді ряд
y n ) також збігається, та для його суми виконується
4
рівність:



n 1
n 1
n 1
  x n   y n     x n    y n .
1.2. Достатні ознаки збіжності рядів
В цьому розділі будемо вважати сі ряди, які ми розглядаємо, є знакосталими, і
навіть рядами з додатними членами. Зрозуміло, що для рядів з від’ємними членами
мають місце аналогічні властивості.
Теоре
(Критерій збіжності знакосталого ряду)
ма 0.
Ряд
 an
- збіжний  послідовність його часткових сум
n
S n   x k - обмежена.
k 1
Доведення. Монотонно зростаюча послідовність збіжна в R тоді і тільки тоді,
коли вона обмежена.
Теорема доведена.
Нагадаємо, що дві послідовності дійсних чисел
( x n ), (a n )
пов’язані
співвідношенням x n  O(a n ) , якщо існує така послідовність ( n )  O (1) (обмежена
послідовність), для якої x n   n a n n  N . В такому разі послідовність (a n )
називають мажорантою для послідовності ( x n ) .
Теоре
(Ознака мажорації)
ма 1.
Нехай послідовність (a n ) є мажорантою для послідовності ( x n ) ,
то: якщо ряд
 an
збіжний, то ряд
умови розбіжності ряду
 xn
 xn
також збіжний; навпаки, з
слідує також розбіжність ряду
 an .
5
Доведення. Нехай ряд
 an
збіжний, тоді послідовність його часткових
n
сум An   a k монотонно зростає і обмежена. З умови x n  O(a n ) слідує, що
k 1
n
S n  O( An ) , де S n   x k . Але тоді послідовність ( S n ) також є обмеженою, крім
k 1
того вона монотонно зростає, а тому є збіжною. З цього і слідує збіжність ряду
 xn .
Якщо ряд
 xn
розбіжний, то послідовність ( S n ) необмежена, але тоді і
послідовність ( An ) також не обмежена, бо вона мажорує послідовність ( S n ) . З
цього слідує розбіжність ряду
 an .
Теорема доведена.
Теоре
(Ознака порівняння)
ма 2.
Якщо ряд
n  N 0 
 a n збіжний, та існує номер
виконуються нерівності
N 0 , починаючи з якого
x n 1 a n 1

, то ряд
xn
an
 xn
також
збіжний.
Доведення. Перепишемо задану нерівність у вигляді:
тому виконується така оцінка
x n  O(a n ) , і за теоремою 1 ряд
x n 1 x n

a n 1 a n
n  N 0  ,
а
xn x N0

 C n  N 0 . А тому x n  a n , тобто
a n a N0
 x n збіжний.
Теорема доведена.
Зі школи добре відомо, що ряд
 qn ,
тобто сума геометричної прогресії, є
збіжним тоді і тільки тоді, коли q  1 . Якщо вибрати в останній теоремі в якості
збіжного ряду геометричну прогресію (тобто 0  q  1), отримаємо такі дві ознаки.
6
(Узагальнена радикальна ознака Коші)
Теоре
ма 3.
Для ряду
 xn
позначимо q  lim n x n , тоді: якщо q  1, то ряд
n 
 x n - збіжний; якщо
q  1 , то ряд
 x n - розбіжний.
Доведення. Нехай q  1 Перепишемо визначення верхньої границі таким
чином: q  lim n x n  lim sup k x k  1. Виберемо число q1 таким чином, щоб
n 
n  k  n
q  q1  1. Тоді існує такий номер N 0 , що n  N 0 sup k x k  q1 . А тому n  N 0
k n
n
x n  q1 . Звідси маємо x n  q1n , а тому x n  O (q1n ) . З того, що ряд
та з теореми 1 слідує, що й ряд
 xn
 q1n
- збіжний
є збіжним.
Якщо q  1 , то виберемо q1 , таке що 1  q1  q . Тоді N 0 : n  N 0
 
sup k x k  q1 . Але тоді існує така підпослідовність x nk , що k  N x nk  q1 . Бо
k n
інакше, якщо остання нерівність виконується тільки для скінченої кількості членів
послідовності, то позначимо через N 1 найбільший номер з них, тоді sup
k  N1 1
k
x k  q1 ,
що суперечить одержаній нерівності. А тоді з існування вказаної підпослідовності
слідує, що lim x n  0 , а це суперечить необхідній умові збіжності ряду, а тому ряд
n 
 xn
- розбіжний.
Теорема доведена.
Нас
(Радикальна ознака Коші)
лідок.
Якщо для ряду
то ряд
Теоре
 xn
 xn
існує границя q  lim
n
n 
- збіжний; якщо q  1 , то ряд
 xn
x n , тоді: якщо q  1,
- розбіжний.
(Узагальнена ознака д’Аламбера)
ма 4.
Якщо для ряду
 xn
q  lim
n 
x n 1
 1 , то ряд
xn
 xn
- збіжний.
7
Доведення. Знову виберемо число q1 таким, щоб виконувались умови:
lim
n 
x n 1
x
 lim sup k 1  q  q1  1.
n  k  n x
xn
k
одержимо, що n  N 0
ряд
Тоді,
починаючи
з
деякого
номера
N0,
x n 1
x k 1
q1n 1
 q1  n , і за теоремою 2
sup
 q1  n  N 0
xn
k n x k
q1
 x n збіжний.
Теорема доведена.
(Ознака д’Аламбера)
Нас
лідок.
Якщо для ряду
то ряд
 xn
 x n існує границя
q  lim
n 
- збіжний; якщо q  1 , то ряд
 xn
x n 1
, тоді: якщо q  1,
xn
- розбіжний.
Доведення. Перша частина безпосередньо слідує з теореми, бо якщо існує
границя послідовності, то вона співпадає із своєю верхньою границею.
Доведемо другу частину. За умовою lim
n 
x n 1
 q  1. Виберемо число q1
xn
таким, щоб виконувались умови: lim
x n 1
 q  q1  1. Тоді, починаючи з деякого
xn
номера N 0 , одержимо, що n  N 0
x n 1
x n 1
q1n 1
 q1  n , і за
 q1  n  N 0
xn
xn
q1
n 
теоремою 2 ряд
 x n розбіжний.
Наслідок доведено.
Теоре
(Про рівнозбіжність рядів)
ма 5.
Нехай послідовність ( x n ) не зростаюча. Тоді ряд
чи розбіжний одночасно з рядом
 2 n x2
n
.
 x n збіжний
8
n
Доведення. Розглянемо такі позначення для часткових сум S n   x i ,
i 1
k
 k   2 j a2 j .
j 0
Якщо n  2 k , то

n

S n   xi  x1   x 2  x3   x 4  x5  x 6  x 7   ...  x 2k  ...  x 2k 1 1 
i 1
 x1  2 x 2  4 x 4  ...  2 k x 2k   k , а тому
Sn   k .
(1)
Якщо n  2 k , то

n

S n   xi  x1   x 2   x3  x 4   x5  x 6  x 7  x8   ...  x 2k 1 1  ...  x 2k 
i 1

1
1
x1  x 2  2 x 4  ...  2 k 1 x 2k   k , тобто
2
2
1
Sn   k .
2
Якщо ряд
(2)
 2 n x2
n
збіжний, то послідовність
 k 
обмежена, а тому
обмеженою є також послідовність ( S n ) , що слідує з нерівності (1), тоді й ряд
збіжним. Якщо ж ряд
 2 n x2
n
 xn є
розбіжний, то відповідна послідовність часткових
сум  k  необмежена, а тому й послідовність ( S n ) також необмежена, що слідує з
нерівності (2). А з останнього слідує, що ряд
 xn
- розбіжний. Повністю
аналогічно в зворотному порядку.
Теорема доведена.
(Збіжність степеневого ряду)
Наслі
док 1.
Степеневий ряд
p  1.

1
np
збіжний, якщо p  1 , та розбіжний якщо
9
Доведення. Якщо p  0 , то розбіжність цього ряду слідує з необхідної
умови збіжності ряду, тобто загальний член ряду не прямує до нуля. Нехай тепер
p  0 , використаємо теорему, розглянемо ряд
геометрична прогресія із знаменником q 
1
2 p 1
2
k
x 2k
2k
1
  kp   k ( p 1) , а це є
2
2
. Цей ряд збіжний при q  1, тобто
при p  1, та розбіжний в іншому випадку.
Наслідок доведено.
Наслі
(Збіжність степенево-логарифмічного ряду)
док 2.

Ряд
1
n ln p n
збіжний при p  1, та розбіжний при p  1 .
Доведення. Знову розглянемо рівнозбіжний ряд, про який йдеться у
відповідній теоремі.

k

2k
2 ln 2

k p

1
ln p 2

1
kp
, а далі залишається скористатися
наслідком 1.
Наслідок доведено.
Теоре
(Ознака Куммера)
ма 6.
Якщо для ряду
 a n існує послідовність
(bn ) додатних чисел
така, що:
1) ряд
1
b
- розбіжний;
n
2) числа v n 
Тоді ряд
a n bn
 bn 1 одного знаку.
a n 1
 an
збіжний, якщо існує l  0 , для якого n  N
v n  l ; якщо ж v n  0 , то цей ряд розбіжний.
10
Доведення. Спочатку розглянемо перший випадок, коли існує l  0 ,
для
якого
виконуються
нерівності:
vn  l  0 .
Тоді
можемо
записати:
la n 1  a n bn  a n 1bn 1 . Записуючи ці нерівності послідовно для n  1,2,..., одержимо:
la 2  a1b1  a 2 b2
la 3  a 2 b2  a 3 b3
............................
la n 1  a n bn  a n 1bn 1
Додамо ці нерівності і будемо мати:
l (a 2  a 3  ...  a n 1 )  a1b1  a n 1bn 1  a1b1 ,
n 1
S n 1   a k 
k 1
і
так
як
l  0,
то
a1b1
 a1 , тобто послідовність ( S n ) обмежена, а тому і збіжна.
a n 1
Нехай тепер v n 
a n bn
 bn 1  0 , тоді можемо записати це у такому вигляді:
a n 1
a n bn  a n 1bn 1 . Продовжуючи це, маємо:
a n 1bn 1  a n bn  a n 1bn 1  ...  a1b1  a n 1 
1
b
слідує розбіжність і ряду
a1b1
, звідки з розбіжності ряду
bn 1
 an .
n
Ознака доведена.
Нас
(Ознака Куммера в граничній формі)
лідок.
Якщо для ряду
 a n існує послідовність
(bn ) додатних чисел
така, що:
1) ряд
1
b
- розбіжний;
n
a b

2) lim  n n  bn 1   l .
n  a
 n 1

Тоді при l  0 ряд
 a n збіжний; а при l  0 , цей ряд розбіжний.
11
Доведення. Якщо l  0 , то N 0 : n  N 0 v n 
a n bn
l
 bn 1   0 , а
a n 1
2
тепер достатньо застосувати ознаку Куммера. Аналогічно для від’ємного l .
Наслідок доведено.
(Ознака Раабе)
Теоре
ма 7.
Якщо для ряду
 a n виконується умова
 a

lim n   n  1  r  R ,
n 
 a n 1

то при r  1 цей ряд збігається, а при r  1 - розбігається.
Доведення. Застосуємо ознаку Куммера, поклавши bn  n , зрозуміло, що при
цьому ряд
vn 
1
b
n

1
- розбіжний. Тоді
n
 a

a n bn
a
 bn 1  n n  (n  1)  n   n  1  1  r  1 , а далі залишається
a n 1
a n 1
 a n 1

використати ознаку Куммера в граничній формі.
Теорема доведена.
Теоре
(Ознака Гаусса)
ма 8.
Якщо для ряду
 a n виконується умова
an


    1n , де
a n 1
n n
 ,  ,   0 - сталі, а послідовність  n  O(1) , то ряд  a n :
-збіжний, якщо   1, або   1,   1;
- розбіжний , якщо   1 , або   1,   1.
Доведення. Випадок   1 безпосередньо слідує з ознаки д’Аламбера. Випадок
  1,   1 - це наслідок з ознаки Раабе. Залишається розглянути випадок
  1,   1. Тобто ми маємо рівність:
an
1 
 1   1n . Застосуємо ознаку Кум
a n 1
n n
12
мера, вибравши в якості послідовності bn  n ln n , як було показано вище,
1
 n ln n
степенево-логарифмічний ряд
vn 
розбіжний. Тоді маємо:
a n bn
1  

 bn 1  1   1n n ln n  (n  1) ln( n  1) 
a n 1
n n 

 (n  1) ln n 
 n ln n
n
 (n  1) ln( n  1) 
 n ln n
n
1

 (n  1) ln 1   .
n

Перший доданок прямує до нуля, а другий до  1 , тому що для логарифму
1 1

можна скористатися відомою формулою еквівалентності: ln 1   ~ . Таким
n n

чином v n  1 , і з ознаки Куммера цей ряд розбіжний.
Теорема доведена.
(Абеля)
Теоре
ма 9.
 an
1. Нехай
довільний розбіжний ряд. Тоді існує така
нескінченно мала послідовність ( n )  n  o(1)  , що ряд
 an n
залишається розбіжним;
 an
2. Нехай
довільний
збіжний
ряд.
Доведення.
1)
1
S n  S n 1


Нехай
n
S n   ak   ,
тоді
n 1
n 1
 an n  
 lim

n
n  k 1
 0 , S 0  0 , доведемо, що ряд
n 

an
S n  S n 1


S k  S k 1  lim
n 1
n 
така
що ряд
залишається збіжним.
Sn  .
і
k 1
n 
існує
bn    ,
нескінченно велика послідовність (bn )
 a n bn
Тоді
S n  S n 1
S n  S n 1


n 1

 an n
Покладемо
залишається розбіжним.

S n  S n 1 
S n   , що й треба було показати.
13
2) Якщо a n  0 , то твердження очевидне. Нехай a1  0 , покладемо
n 

 ak
k  n 1
- n  залишок ряду. З відповідної теореми  n  0 при n   , внаслідок
1
чого і  n  0 . Покладемо bn 


n 1
n 1
 a n bn  
 lim
n 

an
 n   n 1
 n   n 1
 lim
n

n  k 1
  . Тоді маємо
n
 k 1   k
 lim    k 1   k  
 k   k 1 n k 1

 0   n   0   , що й доводить збіжність відповідного ряду.
Теорема доведена.
1.3. Теорема Рімана та інші властивості рядів
Якщо відображення
перестановкою ряду
Теоре
f
N N
- бієкція, то ряд
 a f (n)
називається
 an .
(Збіжність перестановки ряду)
ма 1.
Якщо ряд
 an
збігається абсолютно та має суму S , то будь-яка
його перестановка також збігається та має ту ж саму суму S .
n
Доведення. Нехай Bn   a f ( k )
- часткові суми перестановки ряду, а
k 1
n
C n   a f ( n ) , тоді послідовність (C n ) - монотонно зростає та обмежена числом
k 1

 ak
, а тому ця послідовність збіжна, з чого слідує абсолютна збіжність будь-якої
k 1
перестановки, а тому і проста її збіжність.
З критерію Коші маємо:   0 N : p  N
a N 1  a N  2  ...  a N  p   .
(1)
14
Нехай M - найбільший з індексів, який мають числа a1 , a 2 , ..., a N ,
 a f (n) .
коли вони є членами перестановки
n
n
k 1
k 1
Зрозуміло, що M  N . Розглянемо
довільне n  M , тоді в різниці  n   a k   a f ( k ) , члени ряду з номерами від 1 до
N скорочуються, і залишаються лише члени з номерами, більшими за N . Внаслідок
(1) n  M  n    lim  n  0 , а тому  lim Bn  lim S n   n   S , що й треба
n 
n 
n 
було довести.
Теорема доведена.
Нехай ряд
 an
містить нескінченну кількість як додатних, так і від’ємних
членів, позначимо послідовно через u1 , u 2 ,... - додатні, а через  v1 ,  v 2 ,... - від’ємні
члени цього ряду. Таким чином можна розглянути ряди з додатними членами
та
 un
 vn .
(Про додатну та від’ємну частини ряду)
Теоре
ма 2.
Якщо ряд
одночасно і ряди
обидва ряди
 u n ,  v n . Якщо ж ряд  a n
 a n збігається абсолютно, позначимо
n
n
k 1
k 1
Нехай тепер ряд
збіжність ряду

 an
 w , тоді
n 1
 u k та Vn   v k монотонно зростають та обмежені числом w ,
а тому вони збіжні, що означає збіжність рядів
 v n , то з рівності
збігається умовно, то
 u n ,  v n одночасно розбігаються.
Доведення. Нехай ряд
послідовності U n 
 a n збігається абсолютно, то також збігаються
 an
 un ,  vn .
збігається умовно. Якби збігалися обидва ряди
n
p
q


k 1
k 1
k 1
k 1
k 1
 un ,
 a k   u k   v k  U p  Vq   u k   v k слідує абсолютна
 a n , що суперечить умові. Якщо ж збігається рівно один з двох
15
n
p
q
k 1
k 1
k 1
рядів, то з рівності S n   a k   u k   v k  U p  Vq , де ми маємо рівність
між двома збіжними та однією розбіжною послідовностями, що неможливо. Тому
обидва ряди є розбіжними.
Теорема доведена.
(Необмеженість додатної та від’ємної частини ряду)
Нас
лідок.
Якщо ряд
 an
збігається умовно, то A, B  R
n 0  N
 p, q  N :
u n0 1  u n0  2  ...  u n0  p  A
v n0 1  v n0  2  ...  v n0  q  B
(2
)
Доведення наслідку слідує з того, що треба записати заперечення критерію
Коші. З теореми 2 слідує, що послідовності часткових сум рядів
 u n та  v n
необмежені, з чого все й слідує.
(Рімана)
Теоре
ма 3.
Якщо ряд
 an
збігається умовно, то l  R існує така
перестановка цього ряду
Доведення.
Розглянемо
 a f (n) , яка збігається до l .
lR,
випадок
інші
випадки
розглядаються
аналогічно. Як і раніше розглянемо додатну та від’ємну частини ряду
 un
та
 a n через
 v n . З попереднього наслідку маємо:
p1
p1 1
k 1
k 1
 p1 : U p1   u k  l та U p1 1 
 uk
l.
p1
q2
p1
q2 1
k 1
k 1
k 1
k 1
Аналогічно  q 2 : U p1  V q2   u k   v k  l та U p1  V q2 1   u k 
 vk
l.
16
Продовжимо
U p1  Vq2 1 
цей
p3 1
 uk
 p3 :
процес:
U p1  Vq2 
p3
 uk
l
та
k  p1 1
l.
k  p1 1
Тепер знову знайдемо q 4 і т.д. ми одержали перестановку, при якій
відбувається коливання часткових сум перестановки навколо числа l , при цьому
різниця на кожному кроці не перевищує відповідного значення u pi чи v q j , але з
умовної збіжності ряду
 a n слідує, що загальний член цього ряду прямує до нуля,
а тому прямують до нуля також послідовності (u n ) та (v n ) , з чого слідує, що
різниця між частковою сумою перестановки та числом l прямує до нуля, що й
означає збіжність цієї перестановки до l .
Теорема доведена.
1.4. Поточкова збіжність. Рівномірна норма
Відображення
функціональною

N F ,
де
F
послідовністю
-
(ФП).
множина всіх функцій називається
Значення
відображення
 ( n)  f n
називається n  м членом, та будемо її позначати ( f n ) .
В подальшому, якщо про це не сказано додатково, в цьому розділі будемо
вважати, що усі функції визначені на спільній множині X  R .
Функціональна послідовність ( f n ) називається поточково збіжною до
функції f , якщо x  X
f ( x)  lim f n ( x) . Будемо це позначати як f n  f . У
n 
випадках, коли важливий сам факт поточкової збіжності ФП, а не гранична функція,
будемо це позначати як f n  .
Функціональна послідовність ( S n ) називається функціональним рядом (ФР),
якщо існує така функціональна послідовність ( f n ) , для якої виконується умова:
17
n  N
x  X
n
S n ( x)   f k ( x) . Такий функціональний ряд будемо
k 1
позначати
 f n . Значення
S n називається частковою сумою ФР
 f n , а функція
f n її загальним членом ( n  м членом) функціонального ряду.
Поточковою сумою ФР
 f n на множині X називається поточкова границя
його часткових сум, якщо вона існує. ФР називається поточково збіжним на X ,
якщо його поточкова сума існує та скінчена в кожній точці множини X .
Якщо ФР збігається до деякої функції S , то будемо це позначати
 fn
якщо важливий сам факт збіжності ряду, то позначатимемо це так:
Поточкову суму ряду, якщо вона існує будемо позначати
S,
 fn
.

 fn .
n 1
ФП ( S n ) завжди можна розглядати як ФР
 S n
 S n 1  , S 0  0 .
Для функції f : X  R число sup f ( x)  R називається рівномірною нормою
xD f
функції та позначається f .
(Про рівномірну норму функції)
Теоре
ма 1.
Для сукупності функцій, що мають областю визначення
множину X , рівномірна норма функцій є нормою.
Доведення. Перевір оми аксіоми норми. Її невід’ємність очевидна.
1) f  0  sup f ( x)  0  x  X f ( x)  0  f  0 .
xX
2) f ( x)    f ( x) - очевидно.
3)
x  X
f ( x)  g ( x)  f ( x)  g ( x)  f  g ,
супремуму і одержуємо нерівність трикутника.
Теорема доведена.
далі
переходимо
до
18
Теоре
(Про обмежену функцію)
ма 2.
Функція f : R  R обмежена тоді і тільки тоді, коли f   .
Доведення безпосередньо слідує з означення супремуму. f  sup f ( x)  
xD f
 M  R : x  D f
Теоре
f ( x)  M .
(Рівномірна норма добутку)
ма 3.
Нехай
f : R  R,
g : R  R,
якщо
D f  Dg   ,
то
fg  f  g .
Доведення. x  D f  D g
f ( x) g ( x)  f ( x)  g ( x)  f  g , а далі знову
переходимо до супремуму.
Теорема доведена.
Теоре
(Про рівномірну норму композиції)
ма 4.
Якщо D f  g   , то виконується рівність: f  g  f
Z
, де f
Z
-
звуження функції на множину X  E g  D f .
Доведення. Нехай x  D g та g ( x)  D f . Тоді f ( g ( x))  f ( w) , де w  g ( x)  X
 sup ( f  g )( x)  sup f (W ) звідки й слідує твердження теореми.
xD f  g
wX
Теорема доведена.
1.5 Достатні ознаки рівномірної збіжності
Нехай в цьому розділі виконується умова: всі функції, що розглядаються
визначені на спільній множині X .
19
ФР
 fn
називається нормально збіжним, якщо ряд

f n - збіжний.
(Зв’язок рівномірної та нормальної збіжності)
Теоре
ма 1.
 f n нормально збіжний, то він є рівномірно
Якщо ряд
збіжним.
Доведення. Використаємо критерій Коші: із збіжності ряду
записати:   0 N  : n  N  p  N
ряд
 fn
n p

k  n 1
fk   
n p
 fk
k  n 1


n p

k  n 1
fn
можемо
f k   , а тому
задовольняє рівномірну умову Коші, а тому він є рівномірно збіжний.
Теорема доведена.
(Ознака Вейєрштрасса)
Наслі
док.
Нехай для ФР
ряд
 n
 f n існує така числова послідовність ( n ) , що
- абсолютно збіжний та
f n  O( n ) , тоді ряд
 fn
збігається рівномірно.
Доведення. З відповідної теореми про мажорантну ознаку збіжності слідує, що
ряд

f n - збіжний, а тому ряд
 fn
- рівномірно збіжний.
Теорема доведена.
Теоре
(Рівномірна збіжність рядів, пов’язаних перетворенням Абеля)
ма 2.
Якщо ФП
 g n ( f n 1 
fn )
( fn gn ) 
g 0  0
на
X , то ФР
 f n (g n
 g n 1 )
та
збігаються рівномірно чи не збігаються
рівномірно одночасно.
З тотожності Абеля можемо x  X записати:
20
n

k 1
n 1
f k ( g k  g k 1 )  f n g n   g k ( f k 1  f k ) ,
а
далі
з
лінійності
k 1
рівномірної границі все і слідує.
Теорема доведена.
(Ознака Діріхле-Абеля рівномірної збіжності ФР)
Теоре
ма 3.
Якщо x  X послідовність  f n (x )  монотонна та

 

 sup g k    sup f k  f n   o(1)
 k n
  k n

То ряд
x  X
 g n ( f n 1 
f n ) збігається на X рівномірно.
n p
 g k ( x) f k 1 ( x) 
запишемо:
k  n 1


 sup g k  
 k n

n p
  f k 1 ( x) 
k  n 1
(1)
f k ( x)  
n p
 g k ( x)
k  n 1
f k 1 ( x)  f k ( x) 


f k ( x)    sup g k   f n  p 1 ( x)  f n ( x) 
 k n


 

  sup g k    sup f k  f n   o(1) , а далі залишається використати критерій
 k n
  k n

Коші для рівномірної збіжності ФР.
Теорема доведена.
Теоре
(Ознака Абеля рівномірної збіжності ФР)
ма 4.
Нехай x  X
n  і
послідовність
f n  O(1) , то ряд
 f n (x) 
 f n n  на
монотонна. Якщо ФР
X.

n
n 1
k 1
Доведення. Нехай     n . Покладемо n  N g n    k   . За умовами
теореми


g n  o(1) . Оскільки  sup g k  
 k n

n p
  f k 1 ( x) 
k  n 1
n  2  n  g n  g n 1 , то ряд з ознаки Абеля-Діріхле ряд
f k ( x)   o(1)  O(1)  o(1) , та
 g n ( f n 1 
f n ) збігається
рівномірно. З оцінки f n g n  f n  g n  O(1)  o(1)  o(1) слідує рівномірна збіжність
21
до нуля ФП ( f n g n ) , то з теореми 2 про рівнозбіжність рядів, пов’язаних
перетворенням Абеля, рівномірно збігається також і ФР
 f n (g n
 g n 1 )   f n n .
Ознака доведена.
(Ознака Діріхле рівномірної збіжності ФР)
Теоре
ма 5.
Нехай x  X
f n  o(1) і
n
 k
послідовність
 O(1) , то ряд
k 1
Покладемо n  N
 f n (x) 
монотонна. Якщо ФР
 f n n  на
X.
n


g n    k . Оскільки  sup g k  
 k n

k 1
n p
  f k 1 ( x) 
k  n 1
f k ( x)  
 O(1)  o(1)  o(1) та n  2  n  g n  g n 1 , то з теореми 3 збігається ряд
 g n ( f n 1 
ФП
f n ) , крім того з умови
( fn gn ) ,
 f n (g n
а
тому
з
f n g n  f n  g n  O(1)  o(1)  o(1) слідує, що
теореми
2
рівномірно
збігається
також
ряд:
 g n 1 )   f n n , що й треба було довести.
Теорема доведена.
1.6. Властивості ФП та ФР
Нехай в цьому розділі виконується умова: всі функції, що розглядаються
визначені на деякій спільній множині X .
Теоре
(Ознака Діні для ФП)
ма 1.
Нехай
ФП
( f n ( x))
x [a, b]  X
монотонна
і
fn  f
поточково на множині X . Тоді, якщо n  N f n , f  C ( X ) , то на цій
множині f n  f .
Доведення. Нехай x  X
f n (x) неспадна, покладемо rn ( x)  f ( x)  f n ( x) ,
тоді для ФП (rn ( x)) маємо такі властивості:
22
1) rn  0 , rn  C ( X ) ;
2) rn незростаюча x  X ;
3) x  X rn ( x)  0 при n   .
Треба показати, що rn  0 , що означає sup rn ( x)  0    0 N  :
x X
n  N 
x  X
n 
rn (x)   , але внаслідок не зростання достатньо, щоб N 1 :
rN1 ( x)   x  X , тоді і для усіх більших номерів буде виконуватись така ж
нерівність.
Від супротивного, припустимо, що це не виконується, тобто   0 n  N
умова rn (x)   не виконується на X , а тому x n  X : rn ( x n )   . З теореми
Больцано-Вейєрштрасса x nk : x nk  x 0 при k   . Всі функції rm (x ) неперервні в
точці x 0  X  rm ( x nk )  rm ( x 0 ) . Але з іншого боку m  n k rm ( x nk )  rnk ( x nk )  
з чого слідує, що rm ( x 0 )   , але це суперечить умові: x  X rn ( x)  0 при n   ,
бо в точці x 0 воно не виконується.
Теорема доведена.
Теоре
(Ознака Діні для ФР)
ма 2.
Нехай усі члени ФР

 fn
сума S ( x)   f n ( x)  C ( X ) , то
n 1
неперервні і невід’ємні на X  [a, b] і
 fn  S
на X .
Це є просте переформулювання попередньої теореми для послідовності
n
часткових сум ряду S n ( x)   f k ( x) , з чого все й слідує.
k 1
При
клад.
Дослідити на рівномірну збіжність ФП f n ( x)  x n на множині
 1
X  0,  .
 2
Перевіримо, що виконуються умови теореми Діні.
23
1) x  X f n ( x)  x n  0 при n   ;
2) x  X f n ( x)  x n спадає;


3) 0, x n  C ( X ) .
З теореми 1 маємо висновок f n ( x)  x n  0 на X .
(Перехід до границі в ФР)
Теоре
ма 3.
Нехай для ФР
1)
 fn  S
 fn
виконуються умови:
на X ;
2) n  N lim f n ( x)  bn ;
xa
тоді  lim S ( x) і виконуються рівності:
x a


lim S ( x)   lim f n ( x)   bn
x a
n 1 x a
(знак суми та границі можна
n 1
міняти місцями).
Доведення. 1) Спочатку покажемо, що ряд
 bn
- збіжний. З критерію Коші
для ФР запишемо:   0 N ( ) : n  N ( ) p  N x  X
f n 1 ( x)  ...  f n  p ( x)   . Зробимо граничний перехід при x  a 
bn  1  ...  bn  p   , тобто для числового ряду
 bn
виконується критерій
Коші, а тому він збіжний.
2) Оцінимо в околі точки a різницю:

  S ( x)   bn 
n 1
n

k 1
n
f k ( x)   bk 
k 1


f k ( x) 
k  n 1

 bk
. Виберемо довільне
k  n 1
  0 , тоді із збіжності ряду  bn та з рівномірної збіжності ФР  f n слідує, що їх
n  залишки прямують до нуля (для ФР рівномірно), а тому N ( ) : n  N ( )

 bk   ,
k  n 1

 f k ( x)   ,
k  n 1
але тоді для скінченої кількості доданків, оскільки
24
f n ( x)  bn
n

k 1
x  a,
при
то
x  S (a,  )   X \ {a}
  0
n
f k ( x)   bk    що x  S (a,  )   X \ {a}   3 , що й треба було довести.
k 1
Теорема доведена.
Теоре
(Граничний перехід у ФП)
ма 4.
Нехай ФП f n ( x)  f ( x) на X і n  N  lim f n ( x) ( a n 
гранична точка множини X ), то  lim f ( x) та виконуються рівності:


n 


lim f ( x)  lim lim f n ( x)  lim lim f n ( x) .
x a
x  a n 
n  x  a
Це є переформулювання теореми на випадок ФП.
Наслі
(Неперервність суми ФР та границі ФП в точці)
док 1.
Якщо в умовах теореми 3 (теореми 4) додатково вимагати, щоб:
1) a  X ;
2) n  N функції f n неперервні в точці a , то
функція S  f  буде неперервною в точці a функцією.
Доведення. Розглянемо відповідну рівність з теореми 3.
lim S ( x)  lim
xa


x  a n 1

f n ( x)   lim f n ( x) 
n 1 x  a


n 1
f n (a) 

 bn  S (a) ,
що доводить
n 1
неперервність функції S . Аналогічно доводиться для ФП.
Наслідок доведено.
Наслі
(Неперервність суми ФР та границі ФП на сегменті)
док 2.
Якщо усі члени ФР

 fn  S   fn  f n
n 1
 f n (члени ФП
( f n ) ) неперервні на [a, b] і
 f  , то функція S  C[a, b]  f  C[a, b] .
25
Для доведення достатньо перевірити, що виконуються умови
попереднього наслідку в кожній точці сегменту [a, b] .
(Інтегрування неперервної ФП)
Теоре
ма 5.
Якщо ФП f n  f на [a, b] і n  N f n  C [a, b] , то f n  R [a, b]
і цю ФП можна інтегрувати почленно, тобто
 lim
n 
b
b
a
a
 f n ( x)dx  
lim f (x)dx   f (x)dx .
b
n 
n
a
Доведення. Умова f n  R [a, b] безпосередньо слідує з умови f n  C [a, b] .
З
fn  f
умови
слідує,
що
  0
N ( ) :
n  N ( )
x  [a, b]
f n ( x)  f ( x)   . З теореми 1 f  C [a, b]  f  R [a, b] , а далі легко одержимо:
b

b
b
a
a
f n ( x)dx   f ( x)dx   f n ( x)  f ( x) dx   (b  a) , звідки і слідує потрібна
a
рівність.
Теорема доведена.
Теоре
(Інтегрування ФП)
ма 6.
Якщо ФП f n  f на [a, b] і n  N f n  R [a, b] , то f n  R [a, b]
і цю ФП можна інтегрувати почленно, тобто
 lim
n 
b
b
a
a
 f n ( x)dx  
lim f (x)dx   f (x)dx .
b
n 
n
a
Доведення. Розглянемо деяке розбиття P проміжку [a, b] :
a  x 0  x 1  ...  x m  b . Тоді x, x  xk маємо такі оцінки:
f ( x)  f ( x)  f ( x)  f n ( x)  f n ( x)  f n ( x)  f n ( x)  f ( x ) . З рівномірної
збіжності ФП   0 N ( ) : n  N ( ) x [a, b]  першій та третій доданки не
перевищують  . Тоді можемо записати:  k ( f )   k ( f n )  2 (коливання на k  му
проміжку розбиття), помножимо кожну відповідну нерівність на x k та додамо від
26
1 до k , тоді одержимо: S  S  S n  S n  2 (b  a)  існує таке
розбиття P , для якого S  S    2 (b  a) , з чого слідує інтегрованість за Ріманом
функції f , а відповідний граничний перехід доводиться аналогічно до попередньої
теореми.
Теорема доведена.
(Інтегрування ФР)
Теоре
ма 7.
Якщо ФР
 fn
 S на [a, b] і n  N f n  C [a, b] , то S  R [a, b]
і цей ФР можна інтегрувати почленно, тобто
 b

n 1 a
b


f n ( x)dx     f n ( x) dx   S ( x)dx .

a  n 1
a
b
Це є пере формулювання відповідної теореми 5.
(Диференціювання ФП)
Теоре
ма 8.
Нехай для ФП ( f n ) x  [a, b] n  N f n (x) та ФП похідних
( f n )  на [a, b] , а сама ФП ( f n ( x)) збігається принаймні в одній точці
x 0  [a, b] . Тоді
fn  f
та цю послідовність можна почленно
диференціювати, тобто x  [a, b] f (x) та f n  f  .
Доведення. Спочатку доведемо рівномірну збіжність ФП ( f n ) . З того, що
f n ( x 0 )  та f n  можемо записати:   0N ( ) : n  N ( ) p  N x  [a, b]
f n  p ( x 0 )  f n ( x 0 )   та f n p ( x)  f n ( x)   . Нехай x - довільна точка з [a, b] , а
тому для різниці
f n  p (t )  f n (t ) виконуються усі умови теореми Лагранжа на
проміжку між точками x та x 0 . Тому   [ x0 , x]  [ x, x0 ] , для якої виконуються
умови:
 f n p ( x)  f n ( x)   f n p ( x0 )  f n ( x0 )   f n p ( )  f n ( )( x  x0 ) .
Тоді маємо:
f n  p ( x)  f n ( x)  f n  p ( x0 )  f n ( x0 )  f n p ( )  f n ( )  x  x0     (b  a) . З того,
що остання нерівність справджується для усіх x  [a, b] , то ФП ( f n ) є рівномірно
27
фундаментальною, а тому f n  на [a, b] . Позначимо граничну функцію
через f . Залишається показати диференційованість f , та збіжність f n  f  .
x  [a, b] розглянемо функції: g n (t ) 
f n (t )  f n ( x)
f (t )  f ( x)
, g (t ) 
, де
tx
tx
t  [a, b] \ {x}, а також g n ( x)  f n ( x) . За умовою lim g n (t )  f n ( x) . Розглянемо
tx
оцінку ( t  x ):
g n  p (t )  g n (t ) 
f n  p (t )  f n  p ( x)
tx

f n (t )  f n ( x)
 f n p ( )  f n ( )  f n p  f n  
tx
, крім того g n  p ( x)  g n ( x)  f n p ( x)  f n ( x)  f n p  f n   . Таким чином ФП
( g n ) рівномірно фундаментальна, а тому й рівномірно збіжна. З умови f n  f та з
визначення функцій g n , g , слідує, що g n  g . Таким чином, якщо використати
теорему про граничний перехід у ФП, можна одержати:
lim f n ( x)  lim lim g n (t )  lim lim g n (t )  lim g (t )  f ( x) ,
n 
n  t  x
t  x n 
tx
що
доводить
диференційованість функції f та потрібну збіжність.
Теорема доведена.
Теоре
(Диференціювання ФР)
ма 9.
Нехай для ФП ( f n ) x  [a, b] n  N f n (x) та ФР
[a, b] , а сам ФР
 f n ( x0 )
x 0  [a, b] . Тоді ФР
 fn
 f n 
на
збігається принаймні в деякій точці
S
та цей ФР можна почленно
диференціювати, тобто x  [a, b] S ( x) 
d 
 
  f n ( x)    f n ( x) .
dx  n1
 n1
Пере формулювання теореми 8.
Теоре
(Первісна ФП)
ма 10.
Якщо n  N існує первісна для функції f n , та ФП f n  f , то
f має первісну на [a, b] . Якщо x 0 - довільна точка на [a, b] , і Fn - така
28
первісна функції f n , що Fn ( x0 )  0 , то Fn  F , де F - первісна
граничної функції f , у якої F ( x 0 )  0 .
Доведення. Оскільки Fn  f n , то виконуються умови теореми 8, а тому F :
Fn  F та x  [a, b] F ( x)  lim Fn ( x)  lim f n ( x)  f ( x) .
n 
n 
Теорема доведена.
Теоре
(Первісна ФР)
ма 11.
Якщо n  N існує первісна для функції f n , та ФР
 fn
 s , то
s має первісну на [a, b] . Якщо x 0 - довільна точка на [a, b] , і Fn - така
первісна функції f n , що Fn ( x0 )  0 , то
граничної функції s , у якої S ( x0 )  0 .
Пере формулювання теореми 10.
2. Практичний аналіз збіжності
2.1
2.2
 Fn
 S , де S - первісна
29
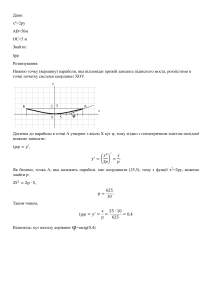
Исходное выражение можно упростить:
Тогда исходный ряд можно представить в виде:
Исследуем сходимость ряда при помощи интегрального признака сходимости Коши.
Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый ряд.
2.3
Областью сходимости степенного ряда является интервал (-R;R), где:
R - радиус сходимости. Вычислим его:
x1 = -1 - 1 = -2
x2 = -1 + 1 = 0
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих
интервалу (-2;0)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -2
Получаем ряд:
Исследуем сходимость ряда при помощи признаков сходимости.
Исходное выражение можно упростить:
30
Тогда
исходный
ряд
можно
представить
в
виде:
Признак Даламбера.
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность
(дополнительные исследования).
Поскольку q = 1, то получаем неопределенность.
Исследуем сходимость ряда при помощи интегрального признака сходимости
Коши.
Рассмотрим несобственный интеграл:
Так как несобственный интеграл сходится, то сходится и исследуемый ряд.
Ряд сходится, значит, x = -2 - точка сходимости.
При x = 0
получаем ряд:
Исследуем
его
сходимость
при
помощи
признаков
сходимости.
Исходное выражение можно упростить:
Тогда исходный ряд можно представить в виде:
Исследуем сходимость ряда при помощи интегрального признака сходимости Коши.
Рассмотрим несобственный интеграл:
Так как несобственный интеграл расходится, то расходится и исследуемый
ряд.
Значит, x = 0 - точка расходимости.
Таким
x∈ [-2;0)
образом,
данный
степенной
ряд
является
сходящимся
при:
31
2.4
2.5
2.6
2.7
2.8
2.9
2.10