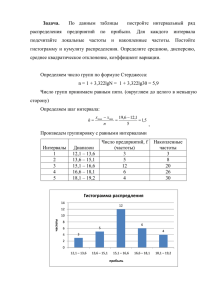
Статистический анализ одномерных выборок - 1,2 Задачи для самостоятельного решения 1. Сравнить риск и возможный доход от вложений средств в два фонда Ожидаемый возврат, % Стандартное отклонение, % Фонд А Фонд В 10 3 7 2,5 Как вы считаете, какой из фондов предпочтительнее? 2. Построить столбиковую и круговую диаграммы доли занятых в различных отраслях региона по следующим данным: Отрасли Количество занятых (тыс.чел.) Промышленность и строительство Сельское хозяйство Сфера обслуживания Сфера интеллектуального труда 40 34 16 24 3. Имеются данные о числе продаж каждоым из 15 случайно выбранных продавцов универмага: 15, 14, 15, 15, 20, 10, 10, 18, 10, 20, 15, 18, 18, 15, 18. По имеющимся данным построить вариационный ряд распределения, дискретный ряд распределения и начертить полигон распределения, вычислить эмпирическую функцию распределения и построить график, построить интервальный ряд распределения числа продаж и начертить гистограмму распределения, вычислить числовые характеристики выборки и дать интерпретацию полученных значений. 4. Дано распределение признака X (случайной величины X), полученное по n наблюдениям. В данной задаче X – месячный доход жителя региона (в руб.); n=1000 (жителей). Менее 500100015002000Свыше 500 1000 1500 2000 2500 2500 ni 58 96 239 328 147 132 Построить гистограмму и эмпирическую функцию распределения X. Найти среднюю арифметическую X , медиану Me и моду M0, дисперсию, среднеквадратическое отклонение и коэффициент вариации V, коэффициенты асимметрии и эксцесса. Дайте интерпретацию полученных значений Xi Теория - Статистический анализ одномерных выборок Пример. Имеются данные о доходах работников некоторой фирмы (тыс.руб.): 2, 4, 7, 3, 1, 1, 3, 2, 7, 3. Построить вариационный ряд, дискретный и интервальный ряды распределения. Найти эмпирическую функцию распределения и построить ее график. Решение. Проведем ранжирование выборки и получим вариационный ряд распределения: 1, 1, 2, 2, 3, 3, 3, 4, 7, 7. Дискретный статистический ряд удобно записывать в следующей таблице xi 1 2 3 4 7 ni 2 2 3 1 2 5 n i 1 2 10 2 10 3 10 1 10 2 10 i 10 5 р i 1 * i 1 Построим эмпирическую функцию по данным дискретного ряда и ее график (рис. 19) по данным таблицы: 0 при x 0; 0,2 при 0 x 2; 0,4 при 2 x 3; * F x 0,7 при 3 x 4; 0,8 при 4 x 10; 1 при x 10; F * x 1 0,8 0,7 0,4 0,2 1 2 3 4 5 6 7 8 9 10 x Эмпирическая функция распределения доходов Для построения интервального ряда сначала определим количество интервалов k =[1 + 3,322 lgn] = [1+3,322 lg 10] = [4,322] = 4 и длину интервалов Запишем интервальный ряд в виде таблицы: Интервалы Частоты [1; 2,5) [2,5; 4) [4; 5,5) [5,5; 7] 4 3 1 2 ∑ Относительные частоты 0,4 0,3 0,1 0,2 ∑ Пример. Определить среднюю цену квартиры в некотором районе г. Перми по имеющимся данным (тыс. руб.): 340, 320, 340, 410, 360, 1580, 365. Решение. По имеющимся данным найдем среднее ̅ ∑ тыс. руб. В качестве моды берем наиболее часто встречающееся значение тыс. руб. для нахождения медианы расположим выборочные значения в порядке возрастания: 320, 340, 340, 360, 365, 410, 1580. Так как , то : тыс. руб. Полученное среднее арифметическое значение не будет являться наиболее типичным значением цены однокомнатной квартиры, т.к. большинство квартир (6 из 7) предлагаются по цене ниже 420 тыс.руб. Следовательно, в этом случае применение среднего арифметического для оценок и выводов приводит к ошибочным и недостоверным результатам. Так, потенциальный покупатель, желающий приобрести квартиру по цене, не превышающую 360 тыс. руб., при принятии решения на основе средней цены, скорее всего, откажется от покупки квартиры в данном районе. В то же время более 85% предложений удовлетворяют его требованиям. Здесь целесообразно использовать медиану, которая равна 360 тыс. руб. В данном случае медиана будет правильнее в качестве показателя, характеризующего наиболее типичное значение из имеющихся данных. Пример. Группировка населения по среднемесячной заработной плате (руб.): 1800, 2070, 2550, 3180, 4400. Решение. Найдем выборочное среднее x по формуле: X x 1 n xi n i 1 1800 2070 2550 3180 4400 2800 5 Определим стандартное отклонение из формулы: S2 S 1 n ( xi x)2 , (1800 2800) 2 (2070 2800) 2 (2550 2800) 2 (3180 2800) 2 (4400 2800) 2 927.34 5 Определим коэффициент вариации по формуле: V S x где V S - стандартное отклонение, x- 100% , средняя величина признака. 927.34 100% 33,1% 2800 Коэффициент вариации не превышает 33%, следовательно, совокупность считается однородной. Пример. Обследование жилищных условий жителей поселка представлено следующим распределением. Охарактеризовать жилищные условия жителей поселка. Количество м. кв. До 5 5-7 7-9 9-11 11-13 13-15 15-17 17-19 19-21 21-23 Свыше 23 100 130 170 300 450 400 330 280 140 120 80 на одного человека Численность жителей, человек Решение. Среднюю величину анализируемого признака – средний размер занимаемой площади на 1 человека – будем определять по формуле средней арифметической взвешенной: Количество Численность Накопленные Центральная м.кв. на одного жителей, частоты варианта хi ср человека человек ni До 5 100 100 4 5–7 130 230 6 7–9 170 400 8 9 – 11 300 700 10 11 – 13 450 1150 12 13 – 15 400 1550 14 15 – 17 330 1880 16 17 – 19 280 2160 18 19 – 21 140 2300 20 21 – 23 120 2420 22 80 2500 24 Свыше 23 - n ni 2500 - Центральные варианты определяются как среднее арифметическое из двух значений интервала, например, (5+7)/2 = 6. Так как первый и последний интервал является открытыми, то величина интервала первой группы принимается равной величине интервала последующей (2), а величина интервала последней группы – величине интервала предыдущей группы (2). Таким образом, условно принимаем: первая группа: 3 – 5 последняя группа: 23 – 25 Средний размер занимаемой площади на 1 человека составит: X х 1 4 100 24 120 34220 13,7 n 2500 1 k ni xi . n i 1 м. кв. Размах вариации представляет собой разность между наибольшим ( ( ) и наименьшим ) значениями вариант, т.е.: . Размах вариации составит: R = 25 – 3 = 22 м. кв. Выборочная дисперсия S2 – это средняя из квадратов отклонений значений признака от его средней арифметической величины. Выборочная дисперсия определяется по формуле: S2 1 n ( xiср x )2 ni n ( xiср )2 ni x 2 1 Выборочная дисперсия составит: S2 1 57317 42 242 13,7 2 22,93 . 2500 2500 Стандартное отклонение – это корень квадратный из выборочной дисперсии. S S2 . Среднее квадратическое отклонение составит: S 57317 22,93 4,8 2500 м. кв. V S 100% . x Коэффициент вариации показывает однородность выбранной совокупности: чем он меньше, Мерой сравнения степеней колеблемости для двух, трех и более вариационных рядов служит показатель, который носит название коэффициента вариации и определяется по формуле: тем более однородна совокупность. Для однородной совокупности он не превышает 33%. Коэффициент вариации составит: V 4,8 100% 35% 13,7 Структурными средними являются мода, медиана, квартили. Мода ( Mo ) – варианта, встречающаяся в изучаемой совокупности чаще всего, т.е. варианта, которой соответствует наибольшая частота. Вычисление моды в интервальном ряду с равными интервалами производится по формуле: Mo xМо h где nMo nMo 1 (nMo nMo 1) (nMo nMo 1) , x Мо – начало (нижняя граница) модального интервала; h ─ величина интервала; nMo1, nMo , nMo1 – частоты пред модального, модального и после модального интервалов. Модальный интервал 11 – 13, так как ему соответствует максимальная частота, равная 450. Воспользуемся данными табл. и рассчитаем моду: Mо 11 2 450 300 12,5 (450 300) (450 400) м. кв. Медиана ( Mе ) – варианта, находящаяся в середине ряда распределения. Расчет медианы для интервального ряда производится по формуле: Mе xМе h где 0,5n n x( Me 1) nMe , xMe – начало (нижняя граница) медианного интервала; h ─ величина интервала; n– сумма накопленных частот ряда; n x ( Me 1) nMe – – накопленная частота вариант, предшествующему медианному; частота медианного интервала. Воспользуемся данными табл. и рассчитаем медиану. В таблице медиана лежит между 1250 и 1251 частотами, а они находятся в сумме накопленных частот, равной 1550, поэтому интервал 13 – 15 является медианным. Определим медиану: 2500 1150 Me 13 2 2 13,5 400 м.кв. Для характеристики социально-экономического явления, отраженного рядом распределения, следует рассчитать первый и третий квартили (второй равен медиане) по следующим формулам, аналогичным медиане: Qi xi i n i / 4 n x(i 1) ni , i 1,3 . Первый квартиль составит: Q1 9 2 2500 400 4 10,5 300 м.кв. Третий квартиль составит: Q3 15 2 3 2500 1550 4 17 330 м.кв. Расчет квартилей позволяет отметить, что 25% жителей имеют до 10,5 м.кв. занимаемой площади на 1 человека, а 25% свыше 17 м.кв. занимаемой площади на 1 человека. Остальные 50% жителей имеют от 10,5 до 17 м.кв. занимаемой площади на 1 человека. Сравнивая среднее значение признака с модой и медианой можно отметить, что их значения довольно близки, но не равны между собой. Следовательно, ряд распределения имеет некоторую ассиметрию, которая может быть определена с помощью меры скошенности по формуле: Sk х Мо S . Мера скошенности составит: Sk 13,7 12,5 0,25 , 4,8 т.е. мера скошенности больше 0, а мода меньше среднего значения признака, это говорит о небольшой правосторонней ассиметрии. Интервальный ряд распределения изобразим с помощью гистограммы. 500 400 350 300 250 200 150 100 50 Свыше 23 21 – 23 19 – 21 17 – 19 15 – 17 13 – 15 11 – 13 9 – 11 7–9 5–7 0 До 5 численность жителей, чел. 450 количество м2 на одного человека Гистограмма распределения жителей по количеству м.кв. на одного человека Вывод: среднее количество м.кв. на одного человека составило 13,7 м.кв.. В данной совокупности жителей наиболее часто встречается количество м.кв. на одного человека, равное 12,5 м.кв.. 50% жителей имеют количество м.кв. на одного человека менее 13,5 м.кв., а 50% жителей – более 13,5 м.кв.. Рассчитанный коэффициент вариации больше 33%, следовательно, данная совокупность является неоднородной. Пример. По группировке населения по среднемесячной заработной плате (руб.) расчитать выборочные характеристики. Группы населения по Количество среднемесячной З.П., руб. человек 1800 – 4400 5 4400 – 13690 15 13690 – 22900 10 ИТОГО: 30 Решение. Группы населения по Количество Середины интервалов (xi) Накопленное среднемесячной З.П., руб. человек 1800 – 4400 5 3100 5 4400 – 13690 15 9045 20 13690 – 22900 10 18295 30 ИТОГО: 30 - - Найдем выборочное среднее x количество человек по формуле: X x 1 k ni xi n i 1 3100 5 9045 15 18295 10 11137,5 руб. 30 Выборочная дисперсия определяется по формуле: S2 S2 1 n ( xi x)2 , (3100 11137,5) 2 5 (9045 11137,5) 2 15 (18295 11137,5) 2 10 30032781,21 . 30 Определим стандартное отклонение из формулы: S S 2 30032781,21 5480,23 руб. Вычисление Mo xМо h моды в nMo nMo 1 (nMo nMo 1) (nMo nMo 1) Mo 4400 9290 интервальном ряду производится по формуле: , тогда получим 15 5 10593.33 руб. (15 5) (15 10) Расчет медианы для интервального ряда производится по формуле: 1 30 5 Me 4400 9290 2 15 Mе xМе h 0,5n n x( Me 1) nMe , 10593.33 руб. Квартили находятся по следующим формулам, аналогичным медиане: Qi xi i n i / 4 n x(i 1) ni , i 1,3 . Квартили делят совокупность на четыре части: 25%; 50%; 75%; 100%, для того чтобы найти первый квартили нужно узнать сколько составляет 25% от 30: 1 30 5 Q1 4400 9290 4 15 30 25% 7.5 . 100% 5948.33 руб. Для того чтобы найти второй квартили нужно узнать сколько составляет 50% от 30: 30 50% 15 . 100% 2 30 5 Q 2 4400 9290 4 15 10593.33 руб. Для того чтобы найти третий квартили нужно узнать сколько составляет 75% от 30: 30 75% 22.5 . 100% 3 30 20 Q3 13690 9210 4 10 15992.5 руб. Мы знаем что 100%=30, найдем четвертый квартиль: 4 30 20 Q 4 13690 9210 4 10 22900 руб. k Определим асимметрии по формуле: As (3100 11137,5) 3 As ni ( xi x ) 3 i 1 5 (9045 11137,5)3 15 (18295 11137,5)3 10 30 5480,233 nS 3 , 6,7 Левосторонняя, значительная асимметрия. Для симметричных распределений может быть рассчитан показатель эксцесса ( Ex ): n Ex ( xi x ) 4 i 1 nS 4 Ex (3100 11137,5) 4 3, 5 (9045 11137,5) 4 15 (18295 11137,5) 4 10 30 5480,233 Плосковершинное распределение. 3 0,23