Лекция № 6. ВЛИЯНИЕ ПРОСТРАНСТВЕННОГО ЗАРЯДА ЭЛЕКТРОННЫХ И ИОННЫХ ПУЧКОВ.

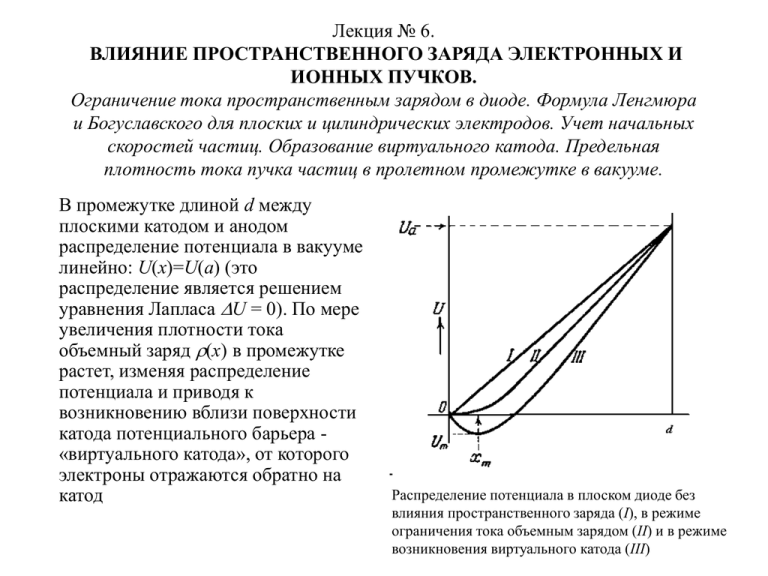
Лекция № 6.
ВЛИЯНИЕ ПРОСТРАНСТВЕННОГО ЗАРЯДА ЭЛЕКТРОННЫХ И
ИОННЫХ ПУЧКОВ.
Ограничение тока пространственным зарядом в диоде. Формула Ленгмюра
и Богуславского для плоских и цилиндрических электродов. Учет начальных
скоростей частиц. Образование виртуального катода. Предельная
плотность тока пучка частиц в пролетном промежутке в вакууме.
В промежутке длиной d между
плоскими катодом и анодом
распределение потенциала в вакууме
линейно: U(x)=U(a) (это
распределение является решением
уравнения Лапласа U = 0). По мере
увеличения плотности тока
объемный заряд (x) в промежутке
растет, изменяя распределение
потенциала и приводя к
возникновению вблизи поверхности
катода потенциального барьера «виртуального катода», от которого
электроны отражаются обратно на
катод
Распределение потенциала в плоском диоде без
влияния пространственного заряда (I), в режиме
ограничения тока объемным зарядом (II) и в режиме
возникновения виртуального катода (III)
Распределения потенциала в промежутке
Для определения распределения потенциала в промежутке необходимо
решать уравнение Пуассона U= -4(x) с учетом того, что плотность тока в
промежутке j = - v. Если считать, что электроны эмитируются с катода с
нулевой скоростью (тепловая энергия эмиссионных электронов много
меньше энергии, приобретаемой в промежутке), то устойчивым является
режим, когда «виртуальный катод» не образуется, а электрическое поле на
поверхности катода равно нулю:
dU
E
dx
x 0
0
При таком граничном условии в режиме ограничения тока объемным
зарядом решением уравнения Пуассона
2
4j
d U
1

dx 2
2e / m U
(здесь учтено, что при начальной нулевой скорости энергия электронов
mv2/2 = eU) является распределение потенциала в промежутке в виде:
x 4/3
U ( x)  U (d )( )
d
Закон «3/2»
В этом случае плотность электронного тока, который можно пропустить
через промежуток ограничена величиной, зависящей от напряжения на аноде
Ua и от расстояния между катодом и анодом d (закон Чайльда-Ленгмюра, или
закона «3/2» :
j 3 / 2 [ А / см 2 ] 
2
9
3/ 2
U
e U a3 / 2
6
a [ В]
 2.33  10
2
me d
d 2 [см]
Для цилиндрических диодов предельная плотность
электронного тока так же зависит от напряжения на
аноде, как степень «3/2», но зависимость от расстояния
между катодом и анодом носит более сложный характер
(как результат решения уравнения Пуассона в
цилиндрических координатах) и описывается r
( a ) ,
специальной функцией Богуславского
rk
2
где ra и rk – радиусы анода и катода соответственно:
J3/ 2
2

9
2e
me
U a3 / 2
2 ra
ra  ( )
rk
l
rk
ra
1
10
100
r
rk
Образование виртуального катода.
В случае, когда начальная скорость эмитированных
электронов не равна нулю, минимум распределения
потенциала будет находиться на некотором расстоянии от
поверхности катода, т.е. возникает так называемый
«виртуальный катод». Это название возникло с точки зрения
места, с которого как бы происходит эмиссия электронов.
Электроны, покидающие катод, как будет показано позднее,
имеют модифицированное распределение максвелла.
V0  0

e
0
xm
Часть электронов, имеющих энергию более высоты потенциального барьера
(значения потенциала в минимуме), продолжают движение к аноду, другая
часть отражается от барьера обратно к катоду. Глубина потенциальной ямы
«виртуальный катода» равна средней кинетической энергии
электронов.
2
d  4j
4j
Уравнение Пуассона с учетом V0 ≠ 0 примет вид:


2
3
V
dx
2e
V0 1 
2 e  m2
2
mV
j
0
Определим из условия:
9 m x m2
4

3


W
x

x
W0


m
 U a  0  

, x  xm

e   d  xm 
e

После интегрирования получим:
  x  
4

W0  x  xm  3


 , x  xm
e
x

 m 
Ua
Транспорт потока заряженных частиц в пролетном промежутке (задача Бурсиана).
Плотность тока заряженных частиц в
пролетном промежутке между
электродами с одинаковым
потенциалом также ограничена из-за
собственного объемного заряда и,
соответственно, потенциала пучка.
Рассмотрим эту задачу (задачу
Бурсиана) на примере потока в
пролетном промежутке длины d ионов
массы M, ускоренных до этого в
плоском диоде потенциалом U0
Экстремальное значение dm соответствует критическому значению максимума
потенциала: Um = (3/4)U0. При возрастании плотности ионного тока дебаевский
радиус пучка уменьшается, потенциал в пролетном промежутке будет возрастать до
Um, затем скачком возникает «виртуальный анод» с Um = U0, от которого произойдет
отражение части ионов обратно в сторону источника, в результате чего ток на
коллектор уменьшится в 4.5 раза.
Транспорт потока заряженных частиц в пролетном промежутке
(задача Бурсиана).
Распределение потенциала в промежутке
задается уравнением Пуассона:
Mi
4
4 j
2e  
   4  
U0  
M 
j i 
 2e 
U0
Введем безразмерные величины:
 

U0
1
i
U0
2

1
1
x
0
x

rd
d
3
M 
4 j  i 
 2e 
MV 


2
e


2
i 0
U0 4
1

4
U0
1
U0
Размерность rd определяется из соотношения:
С учетом j  neV0 получим:
rd 


3
4
M 
4 j  i 
 2e 
1
4
M iV02

4 ne2
 Mi 
4j 

2
e


3
U0 2
1
2
d
2

1
rd2
- дебаевский радиус пучка.
Транспорт потока заряженных частиц в пролетном промежутке (задача
Бурсиана).
Перепишем уравнение Пуассона в безразмерных величинах и домножим на 2   d 
   
1
1 
| 2   d
 2  4
После интегрирования получим
1   C
Константу интегрирования определяем из граничного условия:  | 0  E 0  C  E0  4
С учетом этого
 2  4

1   1  E02
Советский физик В.Р. Бурсиан показал, что решение устойчиво, если
3
При E0  2
т.е.  max 
4
E0 
развивается неустойчивость Бурсиана, и потенциал скачком возрастает до
Распределение потенциала до развития неустойчивости задается
уравнением:

d

4 1   1  E
 d
2
0
d
|0  2
d
 1
Транспорт потока заряженных частиц в пролетном промежутке (задача
Бурсиана).

Последнее уравнение можно переписать в виде:
 
0

d

4 1    1  E02
Условие устойчивости E0  2 соответствует условию на
4 2
d
rd . d m
максимальную длину пролетного промежутка:
3
Экстремальное значение dm соответствует критическому значению
максимума потенциала: Um = (3/4)U0.
При возрастании плотности ионного тока дебаевский радиус пучка
согласно уменьшается, потенциал в пролетном промежутке будет
возрастать до Um, затем скачком возникает «виртуальный анод» с Um
= U0, от которого произойдет отражение части ионов обратно в
сторону источника, в результате чего ток на коллектор уменьшится в
4.5 раза. Таким образом, ток в пролетном промежутке ограничен
3
током Бурсиана:
2
jmax  jБ 
8
9
2e U 0
 8 j3
2
2
Mi d
Транспорт компенсированного потока заряженных частиц (задача Пирса).
Даже в случае скомпенсированного пучка
электронов, когда пространственный
заряд электронов в пролетном
промежутке скомпенсирован ионами
(задача Пирса), возникает ограничение на
максимально возможную плотность тока
из-за неустойчивости, также приводящей
к образованию виртуального катода и
запиранию пучка.
+ +
e
+
+
+
d
Компенсированный поток электронов.
Условием устойчивости на длину пролетного промежутка в случае
скомпенсированного потока является d < rd, а предельная плотность
тока (ток Пирса) равна:
.

2e U 03 / 2 9 2
jП 
4(1  (m / M )
1/ 3
)
m d
2

4
j3 / 2
Транспорт компенсированного потока заряженных частиц
(задача Пирса).
Физическая причина неустойчивости Пирса та же, что и
неустойчивости Бурсиана, – положительная обратная связь
электронов пучка с электронами внешней электрической цепи,
которая возникает, если дебаевский радиус пучка становится меньше
расстояния между электродами. Качественно эти неустойчивости
сродни пучковой неустойчивости, при которой энергия
направленного движения передается в энергию плазменных
колебаний.
2
k

Пучковая неустойчивость возникает, когда kVe  0 , где
Lхар ,
Lхар -характерная длина развития неустойчивости,
0 плазменная частота (частота ленгмюровских колебаний).
Максимальная плотность потока электронов, ограниченная
jП  jmax  enкрит Ve
неустойчивостью Пирса: