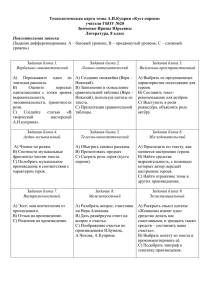
Интерполяция методом обратно взвешенных расстояний (ОВР)
реклама

Блочное моделирование МПИ После создания базы данных и проверки корректности Провели статистический анализ Блок 2 Блок 1 Блок 2 Блок 1 Выделили однородные блоки Создали композиты (рудные пересечения) Отрисовали контуры рудного тела на разрезах Построили каркасную модель Можно приступать к подсчёту запасов Создаётся пустая блочная модель Пустая блочная модель ограничивается каркасом рудного тела В каждом блоке рассчитывается (оценивается) содержание полезного компонента. которое присваевается центральной точке блока Для оценки содержания полезного компонента используются пробы, ближайшие к центроиду блока. 0.637221 0.440068 0.346988 Далее для каждого блока вычисляется объём руды в блоке вес (запасы) руды в блоке вес (запасы) металла в блоке Vруды = _X *_Y *_Z Pруды = V руды* σруды Pметалла = Pруды * Сметалл _Z Cметалла _Y _X Общие запасы по отдельным рудным телам или по месторождению в целом определяются сложением запасов в блоках. + + + + + + + V = ΣVi Qруды = Σpi (руды) + Qметалла = Σpi (металла) Блочная модель позволяет оценить распределение запасов в пределах месторождения, планировать добычу и поддерживать постоянный рудопоток. Когда вы начнёте выполнять подсчёт запасов с использованием блочной модели, у вас возникнет целый ряд вопросов. ? ? ? ? ? ? ? Как выбрать размер блока ? ? ? ? Как ориентировать блоки ? Как выбирать точки для оценки содержания в блоке? Сколько ? Какие? ? ? ? ? Как учитывать блоки, которые пересекают границу рудного тела ? ? ? РУДА ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ПУСТАЯ ПОРОДА Как проверить блочную модель ? Выбор размера блока Размеры блока должны быть связаны с размерами разведочной сети. Для получения несмещенной оценки ? ? ? размер оцениваемых блоков не должен быть меньше половины среднего расстояния между пробами в данном направлении. Чем меньше будет размер блока, тем большее смещение средней оценки мы должны ожидать. Несмотря на это, многие эксперты принимают минимальный размер блоков модели, равный 25 -30% от среднего размера разведочной сети. При выборе размера блока нужно учитывать геометрию рудной залежи ("вписываться" в геологию) и горно-технические требования отработки (минимальная горная мощность, высота уступов карьера, планируемая дневная добыча и др.). Для месторождений планируемых к подземной отработке, особенно жильных рудных тел малой мощности, лучше использовать размер блока близкий к их мощности. Если мы хотим оценить и показать изменение контуров рудных тел при изменении бортового содержания, оценить методы селективной добычи, то лучше использовать размер блока сопоставимый с параметрами внутренней неоднородности (мощностью пустых пород, некондиционных прослоев) Результаты, аналогичные результатам ручного подсчета, будут иметь место при густой и равномерной сети и тогда уже никакое изменение параметров блочной модели не приведет к изменению конечных цифр и геометризации запасов. Обработка блоков, пересекающих границу рудного тела. Две модели: Факторная модель Субблочная модель Блоки,Для пересекающие границу каркаса, каждого блока рассчитывается делятся на более мелкие блоки – субблоки. фактор – доля блока, попадающего В расчёт принимаются субблоки, которые в каркас рудного тела. полностью попадают в пределы каркаса. Если в проекте используются простые каркасные модели без взаимных пересечений, то лучше создавать факторы. Если же в проекте существует несколько взаимно пересекающихся каркасных моделей, то лучше использовать субблоки, хотя размер файлов моделей несколько увеличится. Зато не возникнет путаницы с факторами и не надо будет создавать формул для вычисления факторов блоков в местах пересечения каркасных моделей. Многие операторы предпочитают работать с субблоками, так как они более точно повторяют морфологию рудных тел, что визуально более грамотно. Кроме того, субблочная модель обеспечивает более точный подсчёт объёма Неизвестное значение оценивается Оценка значений блоках. взвешенным средним ближайшихвизвестных значений Методы интерполяции различаются способом (и результатом) вычисления весовых коэффициентов. 1Z s1 n Z2s3 Z S0 i Z Si Z s02 ? i 1 Z S0 - искомое значение для точки S0 n - число опорных точек, находящихся в окрестности искомой точки и используемых в вычислениях. Z3s2 i Пример: 1 2 3 1 Z S1 1 Z S0 Z S2 2 Z S3 3 - весовой коэффициент i -ой точки Z Si - измеренное значение в точке Si n i 1 i 1 1*1 2 *1 3 *1 6 2 111 3 В программах 3D моделирования месторождений полезных ископаемых в настоящее время применяются 2 метода интерполяции: метод обратно взвешенных расстояний и кригинг. Метод ОВР используется: 1. Если нет возможности отстроить вариограммы с распознаваемыми структурами, из которых можно получить достоверные параметры для кригинга. 2. В качестве проверки методов кригинга. Интерполяция методом обратно взвешенных расстояний (ОВР) (IDW – Inverse Distance Weighted) i S1 d i0p n p d i0 d di0 – расстояние между искомой точкой S0 и i-ой опорной точкой, p – показатель степени. i 1 1 1 dp При p = 1: 3 S2 1 1 S1 S3 2 1 1 1 d 1 1 2 2,5 1 1 / 2,5 0,4 2 1 / 2,5 0,4 1 3 2 0,2 1 n 1 2,5 i 1 Оптимальное значение степени p определяется путем минимизации среднеквадратичной ошибки вычислений, которая рассчитывается при перекрестной проверке (каждая опорная точка исключается из вычислений и сравнивается с проинтерполированным значением для этого местоположения). Значения, рассчитанные методом обратных расстояний, не могут выходить за пределы диапазона исходных значений (т.е. не могут быть больше максимального и меньше минимального значения исходных данных) Выбор степени в методе ОВР степень 2 используется, если минерализация имеет умеренно выдержанную непрерывность (стратиформные месторождения цветных металлов) степень 3 используется, если минерализация имеет низкую степень непрерывности (большинство месторождений золота) степени 4 и 5 используются для оценки блока с более эффективным использованием данных о ближайшей пробе (метод «ближайшего соседа») Точки (пробы) для оценки содержания в центроидах блоков выбираются с помощью эллипсоида поиска и контролируются параметрами поиска. Ориентировка эллипсоида поиска задаётся азимутом и углом погружения главной оси и углом наклона плоскости, определяемой главной и большой осями. Степень сжатия – отношением осей. Кроме того, можно организовать поиск проб по октантам Если нет возможности изучить анизотропию содержаний полезного компонента в рудном теле, то ориентировка эллипсоида поиска и степень его сжатия задаются конформно рудному телу: главная ось напрвляется по простиранию рудного тела, а промежуточная по падению (реже наоборот); План Разрез Разрез План Разрез Кригинг. Кригинг - геостатистический метод интерполяции, обеспечивающий наименьшую дисперсию ошибки. (Назван основателем геостатистики, французским математиком Жоржем Матероном в честь своего учителя - южноафриканского горного инженера Дэни Криге (Danie Krige), который впервые применил геостатистику на золоторудном руднике Витватерсранд (Witwatersrand) в ЮАР). Модель кригинга Z x , y m[ x , y ] xy Zx,y – значение в точке с координатами x,y m[x,y] – математическое ожидание ex,y – случайная ошибка в точке с координатами x,y n Интерполяция проводится по формуле Z x' , y i Z i i 1 Формула аналогична методу IDW, однако веса основаны не только на расстоянии между измеренными точками и искомой точкой, но и на распределении опорных точек в пространстве в целом. Вычисление весовых коэффициентов. Для вычисления весовых коэффициентов используется модель вариограммы. 2 # Y 0 [% r03 r1 2 r 23 11 12 13 21 22 23 33 31 32 1 1 1 #3 Y 2 3 r13 1Y # r2 3 r 1 1 1 * 0 1 01 2 02 = 3 03 m 1 # Y 2 r 23 r1 2 0 [% r03 #3 Y 2 3 r13 1Y # r2 3 11 21 31 1 12 22 32 1 13 23 33 1 1 1 1 0 1 * 2 3 m = 01 02 03 1 r