Моментом силы

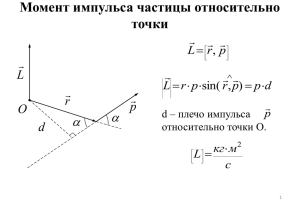
Расписание консультаций
По первой неделе:
Понедельник 16-35 в 217 ауд. (2 корпус)
По второй неделе:
четверг 18-00 в 405 ауд. (3 корпус)
ВоГТУ
Лекция 3
Динамика вращательного
движения (динамика
абсолютно твёрдого тела)
Кузина Л.А.,
к.ф.-м.н., доцент
2012 г.
План
1. Закон динамики вращательного движения
A. Момент силы
B. Момент пары сил
C. Момент инерции
2. Моменты инерции некоторых тел:
A. Кольцо (тонкостенный цилиндр)
B. Толстостенный цилиндр
C. Сплошной цилиндр
D. Шар
E. Тонкий стержень
3. Теорема Штейнера
4. Момент импульса тела. Изменение момента
импульса тела. Импульс момента силы. Закон
сохранения момента импульса тела
5. Работа при вращательном движении
6. Кинетическая энергия вращения
7. Сопоставление величин и законов для
поступательного и вращательного движения
Рассмотривается твердое тело, которое может вращаться вокруг
неподвижной оси. Запишем второй закон Ньютона для отдельной
элементарной массы Δmi, на которые мысленно разбиваем тело:
Fik  mi aik
Fin - нормальная составляющая
равнодействующей силы
Fiê - касательная составляющая
равнодействующей силы
aik    ri
Fik  mi    ri
Fik  ri  mi    ri  ri
Fik  ri  Fi  sin   ri  Fi  li
M i  mi  ri2  
Момент силы
Моментом силы относительно оси называется вектор, направленный
по оси вращения и связанный с направлением силы правилом
буравчика и модуль которого равен произведению силы на ее плечо:
M  F l
M   Í
ì
Плечо силы l относительно оси вращения
– это кратчайшее расстояние от линии
действия силы до оси вращения
В векторной форме
момент силы относительно точки:

  
M  r F

Проекция момента силы
M z  r  F z  F  r  sin   F  l
Момент пары сил
Пара сил – это две равные по
величине и противоположные
по направлению силы, линии
действия которых не
совпадают
Плечо пары сил
Суммарный момент пары сил в проекции на ось,
проходящую через точку О:
M  F2  l2  F1  l1  F  l1  l   F  l1  F  l
Закон динамики вращательного движения
Скалярная величина , равная произведению
массы материальной точки на квадрат ее
расстояния до оси, называется
M i  mi  ri2  
моментом инерции материальной
точки относительно оси ОО:


M i  Ii
Суммируем по всем
элементарным массам, на
которые разбито тело



2
M



m
r
 i
 ii
i

I  mr 2
I   êã  ì
Момент инерции твёрдого
тела:
2

I   mi ri

i
i
 âíåøíèõ

 Mi  M
i
 âíåøí.

M
 I
2
Закон динамики вращательного движения
 âíåøí.

M
 I


M âíåøí .

I

Угловое ускорение тела прямо
пропорционально суммарному
моменту внешних сил и обратно
пропорционально моменту
инерции тела
Аналог для поступательного движения:
 âíåøí .
 F
a
m
Ускорение тела прямо пропорционально
равнодействующей внешних сил и обратно
пропорционально массе тела
Момент инерции I твердого тела является
мерой инертных свойств твердого тела при
вращательном движении и аналогичен
массе тела m во втором законе Ньютона.
Момент инерции I
- зависит от массы тела и от её
распределения относительно оси вращения
- характеризует инертные свойства тела при
вращательном движении

I  mr 2
I   mi ri2

для материальной точки
для твёрдого тела (для системы точечных масс)
i
I   r 2dm   r 2   dV
m
V
для твёрдого тела (если масса распределена непрерывно)
Моменты инерции некоторых тел
1) Кольцо (тонкостенный цилиндр)
I   r 2dm   R 2dm  R 2  dm  mR2
m
m
2) Шар
2
I  mR 2
5
(без доказательства)
m
3)Сплошной цилиндр (диск) dm    dV    h  2  r  dr
R
I   r  dm   r 2   h  2  r  dr
2
m
0
R
I  2     h  r 3dr
0
 r4 
R

I  2     h
 4 

0
I 
    h  R4
2

    R2  h  R2
2
mR 2
I
2

 V  R2
2
m  R2

2
4) Полый (толстостенный) цилиндр
dm    dV    h  2  r  dr
R
2
I   r  dm   r 2   h  2  r  dr
2
m
R
1
R
4 2

r

I  2     h  r 3dr  2 h
 4 
R

R
1
R
I 
I 

h R24  R14
2

V R22  R12
2
2
1
  hR22  R12 R22  R12 
  mR22  R12 
2
2

m R22  R12
I
2

5) Тонкий стержень
m
dm  dr
l
m  r 3 
l
3
2
l
m
m
m
l
ml
I   r 2 dm   r 2  dr   r 2  dr  
  
 3
l
l
l
3
m
0
0
 0 l 3
l
ml 2
I
3
относительно оси, проходящей через конец стержня
относительно оси, проходящей через середину стержня
2
m  l 
  
ml 2
2  2

Ic  2

3
12
ml 2
Ic 
12
Теорема Штейнера
Момент инерции тела относительно
произвольной оси равен сумме
момента
инерции
тела
относительно оси, проходящей
через центр масс параллельно
данной, и произведения массы
тела на квадрат расстояния между
осями:
I  Ic  m  d 2
Для стержня:
I
I  Ic  m  d 2
ml
3

2
ml 2
Ic 
12
ml 2 ml 2
l

 m 
3
12
2
d
2
l
2

 M

I

 d

dt


M d

I
dt




Mdt  Id  d I   dL


L
Момент импульса твёрдого тела
– это
произведение момента инерции твёрдого тела на
угловую скорость:
2
Аналогичен импульсу:


L  I
êã  ì

L 


c
p  mv


Mdt  dL

 dL
M
dt
Аналог
 dp
F
dt


Mt  L
Аналог


F  t  p
Момент импульса материальной точки:
  
L  r  p
L  r  p  sin   mvl
Момент импульса – вектор, направленный по оси вращения по правилу буравчика

Для расчёта момента
 импульса L вращающегося твёрдого тела
найдём сумму L по всем материальным точкам:
i


L   Li   ri  mi  vi   ri  mi    ri      mi  ri2    I
i
i
i
i

Определения эквивалентны:
  
L  r  p



L  I


Mt  L

Mt
Изменение момента импульса тела равно
импульсу суммарного момента внешних
сил.
Это – закон изменения момента
импульса (для незамкнутых систем)
Импульс момента силы
– аналог импульсу силы

F  t
Закон сохранения момента импульса:
 âíåøí .
Если  M
0
Это возможно, если:

 L  const
 âíåøí .
0 )
система замкнута (или  F
у внешних сил нет касательных
составляющих (вектор силы проходит
через ось или центр вращения)
внешние силы параллельны закреплённой оси вращения
Закон сохранения момента импульса:
 âíåøí .
Если  M
0
Примеры:


L  const
У внешних сил нет касательных составляющих (вектор силы
проходит через ось или центр вращения)
– поле центральных сил (гравитация)
Закон сохранения момента импульса:
 âíåøí .
Если  M
0


L  const
Примеры:
Скамья Жуковского
Ñêàìüÿ Æóêîâñêîãî.avi
Закон сохранения момента импульса:
 âíåøí .
Если  M
0
Примеры:
Ãèðîñêîï.avi


L  const
Кошки
используют
закон
сохранения момента импульса:
чтобы приземлиться на лапы, надо
развернуть тело, а для этого кошка
вращает хвостом в другую сторону
Работа при вращательном движении
Пусть тело повернулось
на угол d под

действием силы F

 – угол между силой и перемещением dS

r – радиус-вектор точки приложения силы

Работа силы:
 
dA  F  dS  F cos   dS
dS  r  d
dA  F cos  r  d  F  l  d
M  F l
2
2
1
1
A   dA   M  d

dA  M  d
Кинетическая энергия вращения
Пусть тело вращается относительно закреплённой оси с угловой
скоростью  . Разобьём его мысленно на элементарные массы mi
и просуммируем кинетические энергии:
mi vi2
W  Wi  
i
i 2
vi  ri  

mi 2  ri2  2
W 

 mi  ri2
2
2 i
i


I   mi ri2

i
I 2
W
2
Для катящегося тела:
m  v c2 I   2
Wêèí .  Wïîñò .  Wâðàù 

2
2
Скорость центра масс
Аналогия между поступательным и вращательным движениями
Аналогия между поступательным и вращательным движениями