Международный конкурс научно-технических работ школьников
реклама

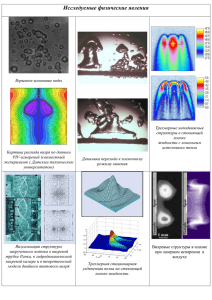
Международный конкурс научно-технических работ школьников “Старт в науку” Направление: физика Тема: «Неустойчивость ламинарного вихревого кольца» Митрохин Антон Лаборатория Непрерывного Математического Образования (ГОУ СОШ №564) 11 класс Научный руководитель: Полищук Г.И., к. ф.-м. н. г. Санкт-Петербург, 2011/2012 учебный год ОГЛАВЛЕНИЕ 1. Введение .............................................................................................................................3 2. Постановка задачи ...........................................................................................................4 3. Постановка экспериментов ............................................................................................4 4. Полученные результаты .................................................................................................5 5. Построение математической модели ............................................................................9 5.1."Энергитическая" модель 5.2. "Волновая" модель 6. Заключение ......................................................................................................................11 7. Использованные источники .........................................................................................12 2 1. Введение. Исследования вихревых колец начались ещё в прошлом веке, когда они рассматривались в качестве модели развивавшейся в то время вихревой теории атомов[1, 2]. В 1970 году С. К. Кроу создал математическую модель описывающую волны, длина которых много меньше диаметра ядра самого вихря (так называемые “короткие волны”), а в 1974 С. Е. Виднелл, Д. Б. Блисс и К. Цай усовершенствовали модель Кроу и смогли обнаружить короткие волны экспериментально. Вихревые кольца (называемые также тороидальными вихрями) и по сей день являются одними из наиболее привлекательных объектов для исследования в гидродинамике. Благодаря тому, что вихревые кольца встречаются довольно часто (зачастую образуются вокруг винта вертолёта, при разбрызгивании жидкости/газа форсункой и т.п), модель, описывающая поведение колец была бы крайне полезна. В [3-5], например, рассмотрен процесс тушения пожаров на нефтяных скважинах с помощью вихревых колец. Но что ещё полезнее, зная заранее количество сгустков, на которое распадётся кольцо в данной среде, можно определить как быстро будут смешиваться две жидкости жидкости при прочих равных условиях (чем больше сгустков, тем быстрее). Рис.1-Тороидальный вихрь. Показано направление циркуляции жидкости в кольце, если бы поток жидкости обтекающей его двигался сверху вниз. Вихревое кольцо можно представить как замкнутый объём завихрённой жидкости имеющий форму тора. Кольцо (называемое ядром вихря) движется вдоль своей оси и окружено медленно вращающимся слоем жидкости, называемым атмосферой вихря. Внутри атмосферы вихря жидкость циркулирует по замкнутым линиям тока, охватывающим тороидальное ядро вихря. Жидкость в ядре вихря также циркулирует, но с несколько большей скоростью[6]. Подробно о структуре вихревых колец можно прочитать, например, в [6-8]. Процесс формирования вихря в жидкости зависит как от метода его генерации, так и его скорости вхождения в жидкость (предполагается, что вихрь создаётся вне жидкости). Процесс формирования “импульсных” вихрей (вихри создаются быстрым выталкиванием жидкости из трубки) ещё до конца не изучен. Так, в работе[7] автор полагает, что формирование вихря связано с его трением о стенки трубок, но в работе[9] эта информация опровергается. В связи со сложностью способа Рис.2-Формирование вихревого кольца (иллюстрация из работы “Проблемы гидродинамики и их математические модели”) 3 формирования кольца “импульсным” методом, в данной работе будут рассматриваться только кольца, полученные падением капли в жидкость с небольшой высоты(5-20 мм). Данный метод довольно прост и рассмотрен, например в работе [7]. На границе между каплей и водой образуется вихревой слой, сворачивание которого и приводит к образованию кольца. При этом всплеск жидкости на поверхности практически отсутствует. Вихрь движется под действием силы тяжести вниз и в результате действий на него сил, появляющихся в результате Рис.3-Распад ламинарного вихревого кольца. Видны шесть сгустков, которые превращаются в новые кольца. эффекта Магнуса, элементы кольца приобретают скорость, направленную перпендикулярно скорости движения кольца. Такое движение неустойчиво, и происходит распад кольца на отдельные сгустки, которые снова превращаются в маленькие вихревые кольца (рис.3). В [10] установлено, что существует два типа вихревых колец. Если число Рейнольдса (v – кинематическая вязкость окружающей среды, U0 – начальная скорость вихревого кольца, D0 – его начальный диаметр) не превосходит 1000, движение кольца происходит в ламинарном режиме. В диапазоне значений 1000<Re<3000 находится область переходных гидродинамических режимов движения кольца, а при Re превышающем значение 3000 движение кольца становится турбулентным. В данной работе будут рассматриваться только ламинарные вихревые кольца. 2. Постановка задачи. Целью данной работы является экспериментальное изучение процесса образования длинных волн (длина которых много больше диаметра ядра вихря) на ядре ламинарного вихревого кольца, так как именно эти волны отвечают за его распад. Вторичной целью является разработка математической модели на основании полученных экспериментальных данных и расчёт длины волны возникающих колебаний с целью предсказания количества сгустков, на которое разделится вихрь. Понятно, что определяющими параметрами распада кольца будет большой и малый радиус тора (R и r соответственно) и V – скорость вихря в момент формирования колебаний, а также параметры самих жидкостей (вязкость, плотность и т.п). 3. Постановка экспериментов. С целью проведения поисковых экспериментов, сбора статистических данных и исследования роста волн была создана экспериментальная установка, позволяющая проводить съёмку вихревого кольца на обычную видеокамеру. Установка состоит из стеклянной камеры, в которой собственно проводится эксперимент, и капельницы, которая создаёт капли заданного размера и падающие с заданной частотой. 4 Стеклянная камера имеет форму параллелепипеда размером 75x75x150 мм (достаточно, для того, чтобы считать движение вихря движением в неограниченной среде) и склеена из плоских кусков стекла. Капельница представляет из себя тонкую полую иголку, из которой торчит проволочка. Проволочка на конце свёрнута в петельку. Жидкость, стекая по проволочке, собиралась на петельке. Соответственно, чем больше была площадь петельки, тем большего размера каплю можно было получить, как следствие получая различные R и r в момент распада. Скорость входа исследуемой капли в жидкость регулируется высотой капельницы над поверхностью жидкости, а также размерами кольца (сила Рис.4-Схематичное устройство экспериментальной установки лобового сопротивления различна). На рис.4 схематично показано устройство экспериментальной установки. В качестве исследуемых жидкостей были использованы: чернила для принтера, “Йодинол”, клей “ПВА”, глицерин (при температуре 50 , чтобы его вязкость не влияла на ход эксперимента). Капли падали в воду. С целью отследить скорость и направление движения жидкости в вихре была применена вода с добавленными в неё мелкими частичками мела (рис.5). Зная время выдержки камеры, скорость движения частичек было легко отслеживать по величине “следа”, который они оставляли за собой на фотографии. Рис.5-Вихревое кольцо из частичек мела. Видна атмосфера вихря. 4. Полученные результаты. В ходе экспериментов было выяснено, что количество капель на которое разделяются два одинаковых кольца совпадает. Но стоит растворить в воде (в которой движется кольцо) немного соли, уменьшив скорость движения кольца (и изменив коэффициент поверхностного натяжения границы раздела воды с кольцом), как количество капель уменьшается (вместе с размерами кольца). Более того, если расположить капельницу выше, увеличив таким образом начальную скорость движения вихря, его размер в момент распада становится больше, как и количество капель после распада. Всё вышесказанное верно если сравнивать кольца из одной жидкости. Если сравнить две жидкости разной плотности но с почти одинаковым К.П.Н с водой (чернила для принтера и “Йодинол” – обе по сути вода в воде), одно кольцо будет двигаться быстрее, но распадутся они при одинаковых размерах, хоть и на разное количество капель. Соответственно, на распад влияет не только размеры кольца в момент распада, но 5 и скорость их изменения до распада (которая определяется скоростью кольца). Для исследования изменения параметров вихря (большего, меньшего радиуса и скорости движения) была написана компьютерная программа, способная находить границы вихря на каждом кадре отдельно и заносить данные на график. Программа была написана на языке Python с использованием библиотеки компьютерного зрения OpenCV. Для определения численных соотношений пикселя и миллиметра (масштаба) в начале съёмки на камеру фотографировался квадрат со стороной 10мм. Рис.6-Пример работы программы. Кольцо движется сверху вниз (съёмка сбоку), результаты измерений отображаются на экране и параллельно наносятся на график. 6 В результате работы программы, для каждого проведённого эксперимента возможно было построить график зависимости большего и меньшего диаметров, а также скорости от времени (с шагом 1/30 с). Рис.7-Зависимость малого диаметра кольца (мм) от времени (1/30 с). Виден момент распада кольца на отметке 54 по времени. “d” вычисляется как “толщина” капли, видимой на экране (показано на рис.6) Рис.8-Зависимость большего диаметра кольца (мм) от времени (1/30 с). “D” вычисляется как разность ширины кольца (капли) и “d”. Таким образом, видно, что капля приняла тороидальную форму примерно к 1/2 секунды (отметке 15) с момента начала отсчёта. 7 Рис.9-Зависимость скорости центра масс кольца (см/c) от времени (1/30 с). Получена дифференцированием пройденного кольцом пути по времени. Видно, что в момент распада скорость практически постоянна (силы Архимеда, тяжести, лобового сопротивления и трения компенсируют друг друга) Помимо собственно графиков, были получены фотографии волны, образующейся на ядре вихря. Видно также, что места образования капель обладают радиальной симметрией относительно центра кольца. Рис.11-Бочкообразные деформации переходят в изгибные. Рис.10-Бочкообразные колебания на ядре вихря Рис.12-Распад кольца. Видно, что расстояния между соседними каплями равны. 8 5. Построение математической модели. Для простоты изначально рассматривалась только энергетическая “выгода” распада. В результате была создана “Энергетическая” модель распада вихревого кольца. 5.1 “Энергетическая” модель. С ростом диаметра кольца площадь его поверхности постепенно увеличивается, и, начиная с некоторого момента времени, состояние “торообразной” формы будет менее устойчивым, чем нахождение в форме нескольких отдельных капель. Другими словами, суммарная поверхностная энергия капель будет меньше, чем поверхностная энергия тора. (При условии, что суммарный объём капель равен объёму тора) В данной модели будем считать, что развал произошёл на N идеальных сфер. В таком случае, верна система: Учитывая, что Соответственно, получается соотношение Где R и r – больший и меньший радиус кольца соответственно. Подставим значения рис.7 и рис.8 в формулу (учитывая, что распад произошёл на 1,8 секунде - отметке 54) В результате эксперимента кольцо развалилось на шесть капель, что очень близко к верхней границе для N. Тем не менее, модель не учитывает скорость движения кольца, а при меньших скоростях это кольцо могло развалиться и на меньшее количество капель. Более того, модель основывалась на энергетической выгоде распада, а значит при 9 небольших коэффициентах поверхностного натяжения, когда поверхностная энергия не играет особой роли, будет давать большую погрешность. 5.2 “Волновая” модель. Для устранения недостатков “энергетической” модели была создана “Волновая” модель распада кольца. Модель основывается на предположении, что в каждый момент движения вихря на ядре присутствуют бочкообразные колебания нескольких длинн волн (Для простоты будем считать их синусоидальными). В зависимости от размеров кольца амплитуды волн некоторых длинн будут расти, а некоторых – затухать. Если удастся посчитать длину волны колебаний максимальной амплитуды в момент распада, можно получить количество капель поделив длину окружности кольца (2πR) на ƛmax (полученную длину волны). В [11] показан проведён расчёт длины максимально быстро растущей волны на бесконечно длинном неподвижном жидком цилиндре. Можно воспользоваться этими результатами с учётом, что вихревое кольцо меняет свои размеры (и соответственно коэффициенты затухания для данной длины волны не постоянны). Формула, полученная автором [11]: Здесь - коэффициент затухания, r – радиус цилиндра, – коэффициент поверхностного натяжения, - плотность жидкости цилиндра, – длина волны, k – константа. Из вывода формулы также очевидно, что при строго положителен. Запишем уравнение зависимости амплитуды А от : , где А0 – амплитуда через время средний радиус в течение , а0 – начальная амплитуда, r0 – . – аналогично. Соответственно, в момент времени n* амплитуда равна Продифференцировав последнее выражения по нулю, можно найти при каких и приравняв значение производной к достигается максимальное значение функции. Проверка модели выполнялась подстановкой эксперементально полученных значений rк в 10 После дифференцирования и приравнивания значения производной к нулю получилось уравнение Для решения уравнения на компьютере использовался метод Ньютона, и погрешность на невязких жидкостях на превышала 19%. Тем не менее, расчёт количества капель с помощью “Волновой” модели довольно сложен, так как перед расчётом необходимо заранее знать зависимость геометрических размеров кольца от времени. 6. Заключение. Обе построенные модели обладают приемлемой точностью и их применение на практике вполне возможно. Тем не менее, не удалось исследовать влияние на процесс образования капель вязкости и, как следствие, построенные модели применимы только к жидкостям с малой вязкостью. С вязкими жидкостями наилучшим образом сходятся предсказания “Энергетической” теории (проверялась на глицерине), но погрешность может достигать 50%. Следует также подчеркнуть, что без теории формирования и развития вихревого кольца теория распада мало применима – в любом случае приходится проводить многочисленные эксперименты и собирать данные для того, чтобы подставить значения в формулы. 11 Использованные источники: 1. Kelvin Lord Philosophical Magazine (34, стр 15, 1867) 2. Kelvin Lord Philosophical Magazine (10, стр 155, 1880) 3. Ахметов Д. Г., Луговцов Б. А., Тарасов В. Ф. Тушение пожаров на газонефтяных скважинах с помощью вихревых колец (Физика горения и взрыва, № 5, стр. 8–14, 1980) 4. Ахметов Д. Г., Тарасов В. Ф. О тушении пожара мощного газового фонтана (Динамика сплошной среды: Сб. науч. тр. АН СССР. Сиб. отд-ние. Ин-т гидродинамики, Вып. 62, стр. 3–10, 1983) 5. Akhmetov D. G., Lugovtsov B. A., Maletin V. A. Vortex powder method for extinguishing fire on spouting gas-oil wells, Prevention of hazardous fires and explosions (Dordrecht etc.: Kluwer Acad. Publ., стр. 319–328, 1999) 6. Ахметов Д. Г. Модель формирования вихревого кольца (ПМТФ том 49, №6, 2008) Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их математические модели. (М.: Наука, 1973) 7. Thomas P. J., Auerbach D. The observation of the simultaneous development of a long- and a short-wave instability mode on a vortex pair (Fluid Mech, том 265, стр 289-302, 1994) 8. Самсонов В. П. Формирование кольцевого вихря в импульсной струе, проникающей через фильтрующий слой. (ЖТФ, 2003, том 29, вып. 15) 9. Стручаев А. И. Изменение характеристик массопереноса при движении вихревого кольца из-за порождения его неустойчивости (Одесский нац. Институт им. Мечникова) 10. Майер В. В. Простые опыты со струями и звуком (М.: Наука, 1985) 11. Милн-Томсон Л. М. Теоретическая Гидродинамика (М.: Мир, 1964) 12. Бэтчелор Дж. Введение в динамику жидкости (М.: Мир, 1973) 13. Волынский М. С. Необыкновенная жизнь обыкновенной капли (М.: Знание, 1986) 14. Бетяев С.К. Гидродинамика: проблемы и парадоксы (1995) 15. Ван-Дайк М. Альбом течений жидкости и газа (М.: Мир, 1987) 16. Фихтенгольц Г.М. Основы математического анализа (М.: Наука, 1968) 17. Флетчер К. Вычислительные методы в динамике жидкостей (М.: Мир, 1991) 18. Laganière R. OpenCV 2 Computer Vision Application Programming Cookbook