АЛГОРИТМ и Формулы В АЛГx

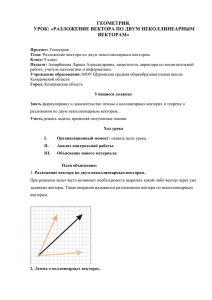
АЛГОРИТМ ПРИЛОЖЕНИЯ ВЕКТОРНОЙ АЛГЕБРЫ
К РЕШЕНИЮ ЗАДАЧ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
I.Выбор подходящей системы координат, запись данных задачи в
координатной форме, М(x,y,z) - общая точка пространства.
II. Перевод данных задачи в векторную форму.
III. Запись условия задачи в векторной форме с помощью символов:
, , ,  и т.п.
IV. Переход от символьной записи условия задачи к векторным
равенствам.
V. Замена векторных равенств координатными.
VI. Проверка соответствия исходныx данныx полученному результату.
Пример. Получить параметричесие и канонические уравнения прямой
l, проходящей через точки А и В.
I. Пусть в декартовой системе координат точки А, В и общая точка
пространства М имеют координаты: A x A , y A , z A  B x B , y B , z B  и М(x,y,z).

II. За направляющий вектор l прямой l  АВ можно принять вектор
A B  xB  x A , yB  y A , z B  z A  m , n , p  и A M  x  x A , y  y A , z  z A  
вектор с началом в точке А.

III. Если точка М(x,y,z)- общая точка прямой l, то векторы A B и A M
коллинеарные векторы, то есть A M  A B .
IV. Условие коллинеарности A M  A B эквивалентно векторному
равенству: A M =t A B , где параметр t определяет положение точки М на
прямой относительно точек А и В.
V. Векторное уравнение  x  x A , y  y A , z  z A  =t m , n , p 
равносильно системе трёх координатных уравнений:
 x  x A  t m,
 x  x A  t m,


 y  y A  t n , то есть  y  y A  t n , - искомые параметричекие уравнения
z  z  t p,
 z  z  t p.
A
A


x  xA y  yA z  z A


.
прямой АВ. Или из A M  A B следует, что
m
n
p
VI. Проверка. M t t 0  A , M t t 1  B. .
 A. Sukhotin, HM, TPU, 2010
ОСНОВНЫЕ ФОРМУЛЫ ВЕКТОРНОЙ АЛГЕБРЫ
I. A B  xB  x A , yB  y A , z B  z A  ,
a  x a i  y a j  z a k   x a , y a , z a 
 xa  t xb ,

x
y
z
II. a b  a  tb   ya  t yb ,  a  a  a  t
xb y b z b

z

t
z
.
b
 a


III. a , b   a b  a  b  cos a ^ b   x a x b  y a y b  z a z b ,
a b  a b  0 ,
a b  0  x a xb  y a y b  z a z b  0
a  a   a a  x a x a  y a y a  z a z a , Пра b  b  cos a ^ b  
cos a ^ b  
ab
a
,
ab
,.
ab
 c  ab sin a^ b   S ab ,

IV. c  a  b  a , b  c a , b c ,

a , b , c   правая тройка векторов..

 
i
j k
c  xa y a z a .
xb y b z b


S ABCD  mod AB AC
xa y a z a
V. a b , c = a , b c , a b , c   a b c  a b c = xb yb zb ,

xc y c z c
c  aa  b  a b c =0,
a b c  Vabc  V ABCS = 1

6


AB AC AS .