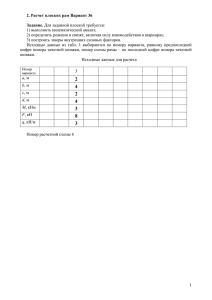
Руководство к решению задач по строительной механике

Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Ю. Б. Гольдштейн
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
Электронная версия
Петрозаводск
Издательство ПетрГУ
2013
УДК 624.04
ББК 38.112
Г635
Рецензенты:
доктор технических наук, профессор В. Д. Харлаб (СПбГАСУ),
кандидат технических наук, доцент Ю. В. Маркаданов (ПетрГУ)
Электронная версия произведения издана при финансовой
поддержке «Программы стратегического развития ПетрГУ на
2012–2016 гг.» в рамках реализации комплекса мероприятий
по совершенствованию учебного процесса
Гольдштейн, Ю. Б.
Г635
Руководство к решению задач по строительной механике
[Электронный ресурс] / Ю. Б. Гольдштейн. – Электрон. дан.
Петрозаводск: Изд-во ПетрГУ, 2013. – 1 электрон. опт. диск
(CD-R); 12 см. – Систем. требования: PC, MAC с процессором Intel 1,3 ГГц и выше; Windows, MAC OSX; 256 Мб. Видеосистема: разрешение экрана 800 × 600 и выше; графический
ускоритель (опционально); мышь или аналогичное устройство.
– Заглавие с этикетки диска.
ISBN 978-5-8021-1746-0
№ гос. регистрации
Приводятся и подробно комментируются примеры решения задач
по всем темам курса «Строительная механика». Предложены условия задач, которые могут быть использованы как преподавателем,
так и студентами для самоконтроля. Предназначается в качестве
учебного пособия для бакалавров и магистров, обучающихся по направлению «Строительство».
Системные требования:
PC, MAC с процессором Intel 1,3 ГГц и выше; Windows, MAC
OSX; 256 Мб. Видеосистема: разрешение экрана 800 × 600 и
выше; графический ускоритель (опционально); мышь или аналогичное устройство. Adobe Acrobat Reader.
ISBN 978-5-8021-1746-0
c Гольдштейн Ю. Б., 2013
c Петрозаводский госуниверситет, 2013
ОГЛАВЛЕНИЕ
ОТ АВТОРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
ЧАСТЬ I. ЗАДАЧИ СТРОИТЕЛЬНОЙ МЕХАНИКИ . . . . . . . . . . . . 8
Задача 1. Построение эпюр усилий в плоской раме . . . . . . . . . . . . 9
Задача 2. Построение эпюр усилий в трехшарнирной арке . . . 10
Задача 3. Расчет составной балки с учетом действия
временной нагрузки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Задача 4. Расчет плоской фермы с учетом действия
временной нагрузки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Задача 5. Определение перемещений в плоской раме . . . . . . . . . 15
Задача 6. Определение перемещений в трехшарнирной арке . 15
Задача 7. Определение перемещений в плоской ферме . . . . . . . 15
Задача 8. Расчет плоской рамы методом сил . . . . . . . . . . . . . . . . . 16
Задача 9. Расчет плоской рамы методом перемещений . . . . . . . 17
Задача 10. Расчет неразрезной балки . . . . . . . . . . . . . . . . . . . . . . . . . 19
Задача 11. Расчет двухшарнирной арки . . . . . . . . . . . . . . . . . . . . . . 21
Задача 12. Расчет статически неопределимой фермы . . . . . . . . 21
Задача 13. Расчет плоской рамы смешанным методом . . . . . . . 22
Задача 14. Расчет плоской рамы на устойчивость . . . . . . . . . . . . 23
Задача 15. Динамический расчет плоской рамы . . . . . . . . . . . . . . 24
Задача 16. Расчет трехшарнирной арки
с помощью программы ЛИРА . . . . . . . . . . . . . . . . . . . . . 26
ЧАСТЬ II. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ
КОНСТРУКЦИЙ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Задача 1. Построение эпюр усилий в плоской раме . . . . . . . . . . .28
Задача 2. Построение эпюр усилий в трехшарнирной арке . . . 38
Задача 3. Расчет составной балки с учетом действия
временной нагрузки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
Задача 4. Расчет плоской фермы с учетом действия
временной нагрузки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Задача 5. Определение перемещений в плоской раме . . . . . . . . . 68
Задача 6. Определение перемещений в трехшарнирной арке . 76
4
Оглавление
Задача 7. Определение перемещений в плоской ферме . . . . . . . 81
ЧАСТЬ III. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
КОНСТРУКЦИЙ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
Задача 8. Расчет плоской рамы методом сил . . . . . . . . . . . . . . . . . 84
Задача 9. Расчет плоской рамы методом перемещений . . . . . . . 95
Задача 10. Расчет неразрезной балки . . . . . . . . . . . . . . . . . . . . . . . .103
Задача 11. Расчет двухшарнирной арки . . . . . . . . . . . . . . . . . . . . . 109
Задача 12. Расчет статически неопределимой фермы . . . . . . . 116
Задача 13. Расчет плоской рамы смешанным методом . . . . . . 122
Задача 14. Расчет плоской рамы на устойчивость . . . . . . . . . . . 130
Задача 15. Динамический расчет плоской рамы . . . . . . . . . . . . .139
ЧАСТЬ IV. РАСЧЕТ КОНСТРУКЦИЙ С ПОМОЩЬЮ
ПРОГРАММЫ ЛИРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
Задача 16. Расчет трехшарнирной арки . . . . . . . . . . . . . . . . . . . . . 150
16.1. О программе ЛИРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
16.2. Об интерфейсе программы ЛИРА . . . . . . . . . . . . . . 153
16.3. Исходная информация к расчету
трехшарнирной арки . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
16.4. Выполнение расчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
16.5. Результаты расчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
СПИСОК ЛИТЕРАТУРЫ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
ОТ АВТОРА
Настоящее пособие, состоящее из четырех частей, предназначено
как для преподавателей строительной механики, так и для студентов бакалавриата и магистратуры, которые обучаются по направлению «Строительство». В основном оно повторяет материал пособия [2],
изданного в 2006 году и используемого для подготовки инженеровстроителей1 . Однако ничто не мешает определенную часть задач предлагать для решения бакалаврам, а более сложные задачи – магистрам,
проходящим обучение при кафедрах строительной механики и строительных конструкций. К материалу, изложенному в издании [2], здесь
добавлены разделы, посвященные расчету конструкций на устойчивость и на гармоническое динамическое воздействие (см. часть III),
и, кроме того, появился раздел, написанный совместно с П. П. Назарьевым, в котором идет речь о расчете конструкций при помощи программного комплекса ЛИРА. Этот комплекс весьма популярен среди
инженеров и многие учебные заведения имеют лицензии на его использование.
В пособии представлены задачи практически по всем разделам курса, однако это не означает, что студент должен решать все из них. Объем и глубина проработки курса определяются учебным планом вуза,
поэтому бакалавру может быть предложен какой-то один набор задач, магистру – другой, а ряд задач останется невостребованным. Да
и бакалавры направления «Строительство» могут проходить обучение
по разным образовательным программам (профилям), в том числе и
таким, которые предусматривают сокращенное изучение строительной механики. Наконец, преподаватель может предоставить студенту
1
Гольдштейн Ю. Б. Строительная механика: Расчетные работы и методические
указания для студентов-заочников специальности "ПГС" /Ю. Б. Гольдштейн. Петрозаводск: Изд-во ПетрГУ, 2006. - 156 С.
6
некий перечень расчетных заданий и предложить ему самостоятельно
выбрать из них определенное число тех работ, которые он (студент)
будет выполнять.
Вычисления, связанные с расчетом силовых конструкций, громоздки, а потому при их проведении активно используется вычислительная
техника. Речь может идти как о программных продуктах специального назначения (ЛИРА, STARK, SCAD и др.), так и об общедоступных
программах типа EXCEL. Весьма удобны и полезны при расчете плоских стержневых систем программы ПОЛЮС и ФЕРМА, разработанные на кафедре механики Петрозаводского государственного университета. Эти программы доступны на сайте кафедры механики ПетрГУ. Используя их, студент может увидеть, каким должен быть ответ
решаемой им задачи. Кроме того, студенты ПетрГУ могут обращаться к программам ЛИРА и STARK, лицензии на право использования
которых в университете имеются.
Как уже отмечалось, данное пособие состоит из четырех частей.
В части I кратко рассказано о постановках тех задач расчета строительных конструкций, которые решаются при помощи аппарата строительной механики. Сопровождающий постановку задачи материал
включает информацию, при помощи которой задается конкретная конструкция для последующего расчета. Такое задание может выдать как
преподаватель, который обучает студента методам расчета силовых
конструкций, так и выбрать сам студент, стремящийся овладеть указанными методами в совершенстве.
Часть II посвящена расчету статически определимых конструкций.
Речь идет о примерах расчета плоской рамы и трехшарнирной арки
на фиксированное силовое воздействие, а также многопролетной балки и плоской фермы на заданные постоянную и временную нагрузки.
Отыскиваются как усилия в названных конструкциях, так и перемещения в них. Особое внимание следует обратить на последовательность
выполняемых операций и на способы контроля правильности вычислений. Важно также внимательно отнестись к правилам построения и
использования линий влияния.
В части III речь идет о расчете статически неопределимых конструкций. Обсуждаются три основные способа раскрытия статической
неопределимости: методы сил, перемещений и смешанный. И здесь
очень важно придерживаться предписанного порядка вычислений и
7
правил их контроля. Особое место занимают задачи устойчивости и
динамики: методологии их решения для статически определимых и
статически неопределимых конструкций одинаковы.
Наконец, часть IV, написанная в соавторстве с П. П. Назарьевым,
посвящена расчету трехшарнирной арки при помощи программы ЛИРА. Эта программа рассчитывает стержневые конструкции, состоящие
только из призматических элементов, поэтому криволинейный контур
арки приходится заменять вписанной в кривую ломаной. Результаты
расчета получаются приближенными, поэтому весьма полезно сопоставление усилий, полученных точно (задача из части II) и при помощи программы ЛИРА.
Приложения к пособию содержат все таблицы и рисунки, при помощи которых формируются исходные данные для задач, рекомендуемых для самостоятельного решения. На эти таблицы и рисунки, расположенные, разумеется, и в основном тексте пособия, идут постоянные
ссылки, поэтому полезно иметь возможность открывать цитируемый
материал в отдельном окне. Что же касается ссылок на те или иные
страницы пособия, то переход к ним и обратно легко осуществляется
средствами программы Adobe Reader, предназначенной для работы с
файлами формата pdf.
ЧАСТЬ I. ЗАДАЧИ СТРОИТЕЛЬНОЙ МЕХАНИКИ
В курсе «Строительная механика» излагаются методы расчета стержневых конструкций на прочность, жесткость и устойчивость. Изучение этой дисциплины следует начинать с проработки теории по учебникам и учебным пособиям [1, 3, 4] и анализа приводимых в них примеров и задач. По важнейшим разделам курса предусматривается выполнение индивидуальных расчетных заданий типа тех, о которых идет
речь в настоящем пособии.
Исходные данные для выполнения расчетных работ выбираются из
таблицы вариантов в соответствии с учебным шифром студента, который состоит из трех цифр и назначается преподавателем. В каждой
расчетной работе выбирается схема, номер которой совпадает с последней (третьей) цифрой шифра. Значения размеров и нагрузок приводятся в таблице исходных данных – своей для каждой расчетной работы. Сперва в таблице выбирается строка, имеющая номер первой цифры шифра, и из столбцов, объединенных подзаголовком «По первой
цифре шифра», выписываются соответствующие исходные данные. Затем в таблице вариантов выделяется строка, номер которой совпадает
со второй цифрой шифра, и исходные данные выписываются из столбцов, объединенных подзаголовком «По второй цифре шифра». Наконец, из строки с номером последней цифры шифра студента берутся
оставшиеся исходные данные, причем используются столбцы, озаглавленные «По последней цифре шифра». Например, если шифр студента
843, то во всех расчетных работах выбирается та схема конструкции,
которая имеет номер 3. При выполнении же первой расчетной работы
его исходными данными будут (см. табл. 1 на с. 10):
l1 = 3, 5 м, l2 = 3 м, l3 = 3, 5 м, l4 = 4, 5 м, l5 = 2 м, q1 = 1, 5 кН/м,
q2 = 1, 5 кН/м, q3 = 2, 5 кН/м, P1 = 8 кН, P2 = 11 кН.
Другие примеры выбора исходных данных, а также образцы выполнения расчетных работ приводятся в части II этого пособия.
Расчетное задание, выдаваемое преподавателем, может содержать
одну или две задачи из приводимого ниже перечня задач.
Задачи строительной механики
9
Задача 1. Построение эпюр усилий в плоской раме
Для рамы (рис. 1), выбранной согласно последней цифре шифра,
требуется построить эпюры усилий M , Q и N от заданной постоянной
нагрузки. Исходные данные берутся из табл. 1.
10
Задачи строительной механики
Указания
1. На схеме рамы (см. рис. 1) рядом с каждым стержнем указан
номер, при помощи которого назначается его (стержня) длина: стержни с номерами 1, 2, . . . , n имеют, соответственно, длины l1 , l2 . . . , ln ,
приводимые в табл. 1.
2. Нагрузка q1 прикладывается к одному из стержней, имеющему
1-й номер (любому). Нагрузка q2 прикладывается к любому из стержней с номером 2. Аналогично, нагрузка q3 прикладывается к одному
из стержней с номером 3. Если загружаемый стержень горизонтален,
то нагрузка направляется вертикально вниз, если же нагрузка прикладывается к стойке, ее направляют в любую сторону по горизонтали.
3. Сила P1 прикладывается по выбору студента к шарниру A или
к шарниру B и направляется вертикально вниз. Сила P2 прикладывается в середине любой стойки рамы в горизонтальном направлении.
Задача 2. Построение эпюр усилий в трехшарнирной арке
Для трехшарнирной арки (рис. 2), выбранной согласно последней
цифре шифра, требуется построить эпюры усилий M , Q и N от заданной постоянной нагрузки. Исходные данные берутся из той же самой
таблицы, которая использовалась при выборе исходных данных для
расчета рамы, т. е. из табл. 1.
Задачи строительной механики
11
Задача 3. Расчет составной балки с учетом
действия временной нагрузки
Для статически определимой многопролетной балки, выбранной
согласно последней цифре шифра при помощи рис. 3, требуется:
1. Взять необходимые данные для расчета из табл. 2.
12
Задачи строительной механики
2. Построить огибающую эпюру изгибающих моментов, учитывая,
что временная равномерно распределенная нагрузка интенсивностью
p может занимать любое положение на конструкции. Воздействия P ,
q, T являются постоянными.
Задачи строительной механики
13
3. Построить линии влияния поперечных сил в сечениях, номера
которых отмечены на схеме балки штрихом, и найти с их помощью
усилия Q от постоянной нагрузки.
Указание. На схеме балки (см. рис. 3) рядом с каждым стержнем
приведен номер, при помощи которого по табл. 2 устанавливается его
длина. Если номер участка отмечен штрихом, его длина уменьшается
в 5 раз.
Задача 4. Расчет плоской фермы с учетом действия
временной нагрузки
14
Задачи строительной механики
Для фермы (рис. 4, табл. 3), выбранной согласно последней цифре
шифра, требуется:
1. Определить усилия во всех стержнях от постоянной нагрузки интенсивностью q, равномерно распределенной вдоль пояса указанного
в табл. 3.
Задачи строительной механики
15
2. Найти расчетные усилия в стержнях фермы, учитывая временную равномерно распределенную нагрузку интенсивностью p.
Указание. При решении задачи использовать симметрию фермы,
вычисляя усилия в стержнях только ее половины (например, левой).
Задача 5. Определение перемещений в плоской раме
Для рамы, эпюры усилий в которой были построены при решении задачи 1 (см. рис. 1 и табл. 1), требуется найти вертикальное и
горизонтальное перемещение одного из шарниров: A или B (по выбору студента), а также угол поворота поперечного сечения, к которому
приложена сила P2 .
Отношение ρ изгибной жесткости EIс стоек к изгибной жесткости EIр горизонтальных стержней выбирается из табл. 4 по последней
цифре шифра.
Задача 6. Определение перемещений в трехшарнирной арке
Для арки, эпюры усилий в которой были построены при решении
задачи 2 (см. рис. 2 и табл. 1), требуется, используя среду Excel, найти
взаимный угол поворота сечений, примыкающих к замковому шарниру. Сравнить значения перемещений, полученные с учетом влияния
всех трех усилий и с учетом влияния только изгибающих моментов.
Считать, что арка имеет постоянное поперечное прямоугольное сечение. Отношение ширины сечения к его высоте равно величине ρ (по
табл. 4), а отношение высоты сечения к пролету арки – 0,02. Коэффициент Пуассона принять равным 0,25, а модуль упругости – 108 кН/м2 .
Задача 7. Определение перемещений в плоской ферме
Для фермы, усилия в которой были найдены в ходе решения задачи 4 (см. рис. 4 и табл. 3), требуется найти вертикальное перемещение
центрального узла грузового пояса от постоянной нагрузки. Осевые
жесткости стержней фермы одинаковы.
16
Задачи строительной механики
Задача 8. Расчет плоской рамы методом сил
Для рамы (рис. 5, табл. 5), выбранной согласно последней цифре шифра, требуется построить эпюры усилий M , Q, N от заданной
нагрузки, используя метод сил. Через ρ в табл. 5 обозначено отноше-
Задачи строительной механики
17
ние изгибной жесткости стоек к изгибной жесткости горизонтальных
стержней (ригелей). Воздействия q и P прикладываются по выбору
студента так, чтобы загруженными были один из ригелей рамы и одна из ее стоек. Нагрузка на ригеле направляется вертикально вниз,
нагрузка на стойке – в любую сторону по горизонтали. Сила P прикладывается в середине стержня.
Задача 9. Расчет плоской рамы методом перемещений
18
Задачи строительной механики
Для рамы (рис. 6, табл. 6), выбранной согласно последней цифре
шифра, требуется построить эпюры усилий M , Q, N от заданной нагрузки, используя метод перемещений. Через ρ в табл. 6 обозначено
отношение изгибной жесткости стоек к изгибной жесткости ригелей.
Задачи строительной механики
19
Воздействия q и P прикладываются по выбору студента так, чтобы
загруженными были один из ригелей рамы и одна из ее стоек. Нагрузка на ригеле направляется вертикально вниз, нагрузка на стойке – в
любую сторону по горизонтали. Сила P прикладывается в середине
стержня.
Дополнительное требование к расчетным схемам 8 и 9 на рис. 6:
загружать стойку с номером 2 нельзя.
Задача 10. Расчет неразрезной балки
Требуется построить огибающую эпюру изгибающих моментов для
статически неопределимой неразрезной балки постоянного сечения,
выбранную по последней цифре шрифта из схем балок, приведенных
на рис. 7. Временная равномерно распределенная нагрузка интенсивностью p, направленная вертикально вниз, может занимать любое положение на конструкции. Постоянные воздействия P1 , P2 , q1 , q2 даны
на расчетной схеме. Сосредоточенные силы прикладываются или на
свободном конце консоли, или в середине загружаемого пролета. Значения названных воздействий выбираются при помощи табл. 7.
Указания
1. Длина стержня, номер которого на схеме балки отмечен штрихом, уменьшается в 5 раз. На это требование следует обратить особое
20
Задачи строительной механики
внимание, ибо длина консоли (т. е. выступающего участка) в реальных
конструкциях всегда несоизмеримо меньше любого пролета балки.
2. Решать задачу можно любым методом, т. е. как методом сил,
так и методом перемещений. Целесообразно использовать тот метод,
который приводит к меньшему числу основных неизвестных.
Задачи строительной механики
21
Задача 11. Расчет двухшарнирной арки
Требуется построить эпюры усилий M , Q и N в двухшарнирной
арке постоянного сечения, отличающейся от арки, усилия и перемещения которой были найдены при решении задач 2 и 6, тем, что в ней
отсутствует замковый шарнир (см. рис. 2, табл. 1 и 4). Сопоставить
максимальные по модулю изгибающие моменты и продольные силы в
трехшарнирной и в двухшарнирной арках.
Задача 12. Расчет статически неопределимой фермы
22
Задачи строительной механики
Требуется найти усилия в стержнях четырежды статически неопределимой фермы при действии постоянной нагрузки. Схема фермы выбирается при помощи рис. 8 по последней цифре шифра. Осевые жесткости у всех неопорных стержней фермы одинаковы.
Указания
1. Все размеры фермы и постоянную нагрузку на нее взять такими
же, что и при решении задачи 4, т. е. из табл. 3.
2. Расчет фермы выполнять с учетом симметрии. Основную систему выбрать так, чтобы она совпадала с конструкцией, изображенной
на рис. 4.
Задача 13. Расчет плоской рамы смешанным методом
Для рамы (рис. 9, табл. 8), выбранной согласно последней цифре
шифра, требуется построить эпюры усилий M , Q, N от постоянной
нагрузки. Через ρ в табл. 8 обозначено отношение изгибной жесткости стоек к изгибной жесткости ригелей. Равномерно распределенная
нагрузка интенсивностью q размещается на любом из ригелей рамы,
а сосредоточенная сила P – в середине другого ригеля (по выбору
студента). Оба воздействия направляются вертикально вниз.
Задачи строительной механики
23
Задача 14. Расчет плоской рамы на устойчивость
Требуется выполнить расчет на устойчивость рамы, которая использовалась при решении задачи 9 (см. рис. 6 и табл. 6). Заданными
считаются как сама конструкция, так и продольные усилия Ni во всех
24
Задачи строительной механики
стержнях конструкции, где i – номер стержня по рис. 6. Эти усилия задаются формулами: N1 = k1 ql1 , N2 = k2 ql2 , N3 = k3 ql3 , N4+ = k4 ql4 .
Обозначение N4+ говорит о том, что продольная сила в стержне 4
(и только в нем) является растягивающей. Множители ki берутся из
табл. 9. На рис. 6 каждая рама имеет два стержня с одинаковыми
номерами. На одном из них (любом, по выбору студента) принимается усилие, вычисленное по формуле Ni = ri qli , а на другом – вдвое
бо́льшая сила. Расчет на устойчивость состоит в определении критической нагрузки на конструкцию в целом и нахождении коэффициентов
приведенной длины для каждого сжатого стержня.
Задача 15. Динамический расчет плоской рамы
Задачи строительной механики
25
Для невесомой конструкции, взятой из рис. 10 по последней цифре
шифра, требуется построить огибающую эпюру изгибающих моментов
при действии гармонической возмущающей силы. Исходные данные
выбираются при помощи табл. 10.
Двигатель, ротор которого при своем вращении порождает гармоническую возмущающую силу, расположен в середине горизонтального стержня (ригеля), т. е. в том месте, в котором на рис. 10 изображена
масса m.
26
Задачи строительной механики
Указания
1. Принять l = 1м, после чего установить длины стержней конструкции по формуле l = ki · l, где i = 1, 2, 3, 4 – номер стержня.
Коэффициенты ki приведены в табл. 10.
2. Принять изгибную жесткость стоек равной величине EI, а изгибную жесткость ригелей – величине kEI. Числа EI и k содержатся
в табл. 10.
3. Принять массу ротора равной величине k0 · m (см. табл. 10).
4. Круговую частоту вращения ротора принять равной величине
0, 7ω1 , где ω1 – частота основного тона собственных колебаний.
5. Эксцентриситет e центра массы m положить равным величине
10−3 · min li , где min li – длина самого короткого стержня рамы.
6. При определении спектра частот собственных колебаний рамы
используются единичные перемещения по направлению возможных
перемещений массы. Такие перемещения следует вычислить при помощи любой программы, обеспечивающей статический расчет стержневой конструкции. Перечень программ, к которым можно обращаться
при выполнении расчетных заданий по строительной механике, приведен на страницах 5–6.
Задача 16. Расчет конструкций с помощью программы
ЛИРА
При решении задачи 2 вручную была рассчитана трехшарнирная
арка на заданное статическое воздействие. Требуется выполнить расчет этой же конструкции при помощи программного комплекса ЛИРА
и сравнить полученные результаты с результатами, найденными ранее.
ЧАСТЬ II. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ
КОНСТРУКЦИЙ
28
Статически определимые конструкции
В этом разделе приводятся образцы решения задач 1–7, о которых
шла речь в части I настоящего пособия. Исходные данные для каждой
работы брались из таблиц 1–10 по шифру 843, однако схемы рассчитываемых конструкций принимались по рис. 11.
Задача 1. Построение эпюр усилий в плоской раме
Условия задачи приводятся на с. 9–10.
1.1. Расчетная схема . Вычерчивается по данным табл. 1 и рис. 11,
отвечающим шифру 843. Длины стержней взяты из таблицы 1 по их
номерам на схеме рамы, нагрузка приложена в полном соответствии
со сказанным в примечаниях 2–3 к тексту задания (см. с. 10). Горизонтальную силу P2 можно было бы приложить и в середине стойки, но
в данном случае она размещена на одном уровне с нижним ригелем.
1.2. Опорные реакции. Изображается расчетная схема рамы со всеми заданными нагрузками и опорными реакциями, направленными
произвольно. При этом учитывается, что в неподвижной шарнирной
опоре реактивная сила может быть разложена на две составляющие,
а реакция подвижной опоры (опорного стержня) ортогональна плоскости скольжения. На схеме указываются равнодействующие Si = qi li
равномерно распределенных воздействий, где qi и li – интенсивность
нагрузки и длина загружаемого элемента рамы: S1 = 1, 5·3, 5 = 5, 25 кН,
S2 = 1, 5 · 3 = 4, 5 кН, S3 = 2, 5 · 3, 5 = 8, 75 кН.
При помощи расчетной схемы составляются условия равновесия
конструкции и ее отсекаемых частей. Например, запись ΣMBпр = 0 говорит о том, что через шарнир B проводится разрез и рассматривается
29
Задача 1
равновесие правой отсеченной части конструкции:
ΣMBпр = 0: R5 · 3, 5−5, 25 · 1, 75 = 0 → R5 = 2, 62 кН.
Далее:
ΣMC = 0: R3 · 6 − 11 · 3, 5 − 4, 5 · 1, 5 − 8, 75 · 1, 75 − 8 · 10, 5−
−5, 25 · 12, 25 + R5 · 14 = 0.
После подстановки сюда величины R5 = 2, 62 кН и выполнения вычислений получится, что R3 = 28, 69 кН.
ΣMD = 0: R2 · 6 + 11 · 3, 5 − 4, 5 · 4, 5 + 8, 75 · 1, 75 + 8 · 4, 5 +
+ 5, 25 · 6, 25 − R5 · 8 = 0.
Остается учесть, что R5 = 2, 62 кН, и найти R2 = −13, 56 кН.
ΣMAлев = 0: R1 · 5, 5 + R2 · 3 − 11 · 2−4, 5 · 1, 5 = 0.
Так как R2 = −13, 56 кН, то R1 = 12, 62 кН.
ΣMAпр = 0 : R4 · 5, 5 − R3 · 3 − 8, 75 · 3, 75 + 5, 25 · 9, 25 − R5 · 11 = 0.
Отсюда при R3 = 28, 69 кН и R5 = 2, 62 кН следует: R4 = 7, 13 кН.
Условия равновесия ΣX = 0 и ΣY = 0 служат для проверки вычислений.
ΣX = 0: − R1 + 11 + 8, 75 − R4 = 0 →
30
Статически определимые конструкции
−12, 62 + 11 + 8, 75 − 7, 13 = −19, 75 + 17, 95 = 0.
ΣY = 0: − R2 + 4, 5 − R3 + 8 + 5, 25 − R5 = 0 →
13, 56 + 4, 5 − 28, 69 + 8 + 5, 25 − 2, 62 = 31, 31 − 31, 31 = 0.
Реакции найдены правильно.
Теперь расчетная схема рамы перечерчивается заново. На ней, помимо активной нагрузки и найденных значений опорных реакций, указываются еще и номера расчетных сечений, т. е. сечений, в которых
будут вычислены усилия M , Q и N . К расчетным относят сечения,
расположенные вокруг мест приложения сосредоточенных и распределенных воздействий, а также шарнирных и жестких узлов – промежуточных и опорных. Эти сечения разбивают контур рамы на участки (в данном случае таких участков 8). Удобно граничным сечениям
участков присваивать номера, идущие друг за другом. Именно так выполнена нумерация расчетных сечений на приводимой ниже расчетной
схеме.
1.3. Усилия в расчетных сечениях. Для вычисления усилия в некотором сечении k конструкции необходимо выполнить в нем разрез и
рассмотреть равновесие одной из отсеченных частей. Обычно рассматривают равновесие той части, на которую действует меньшее число нагрузок. Кроме внешних воздействий, т. е. заданной активной нагрузки
и вычисленных реакций опор, к отсеченной части в месте разреза прикладываются усилия Mk , Qk и Nk . При этом:
– изгибающий момент Mk направляется произвольно;
– поперечная сила Qk прикладывается так, чтобы она вращала отсеченную часть конструкции по часовой стрелке;
31
Задача 1
– продольная сила Nk направляется так, чтобы ось стержня растягивалась.
Для усилий Qk и Nk указанные выше направления положительны.
Знак усилия Mk несуществен, однако эпюра изгибающих моментов
откладывается со стороны растянутого волокна каждого стержня.
Для определения усилий Mk , Nk и Qk записывают следующие условия равновесия отсеченной части конструкции:
ΣMkотс = 0,
ΣPτотс = 0,
ΣPνотс = 0,
где ΣMkотс – сумма моментов всех активных и реактивных сил, приложенных к отсеченной части системы, относительно центра тяжести сечения k (точки k), ΣPτотс – сумма проекций названных сил на направление касательной к оси стержня
в точке k, ΣPνотс – сумма проекций этих же сил на
нормаль к оси стержня в точке k, т. е. на направление поперечного разреза.
Теперь можно перейти к вычислениям.
Сечение 1
ΣM1отс = 0: M1 = 0;
ΣPτотс = 0: N1 −13, 56 = 0 → N1 = 13, 56 кН;
ΣPνотс = 0: Q1 −12, 62 = 0 → Q1 = 12, 62 кН.
Сечение 2
ΣM2отс = 0: M2 −12, 62 · 3, 5 = 0 → M2 = 44, 18 кНм.
Так как величина M2 положительна, то в сечении
2 растянуты волокна, которые растягивает этот момент на рисунке, т. е. правые.
ΣPτотс = 0: N2 −13, 56 = 0 → N2 = 13, 56 кН;
ΣPνотс = 0: Q2 −12, 62 = 0 → Q2 = 12, 62 кН.
Сечение 3
ΣM3отс = 0: M3 = 44, 18 кНм.
32
Статически определимые конструкции
ΣPτотс = 0: N3 = 13, 56 кН; ΣPνотс = 0: Q3+11−12, 62 = 0 → Q3 = 1, 62 кН.
Усилия M3 и N3 подсчитывать не было необходимости, ибо и без того
ясно, что M3 = M2 и N3 = N2 .
Сечение 4
ΣM4отс = 0 : M4 +11 · 2−12, 62 · 5, 5 = 0 →
M4 = 47, 43 кНм.
Теперь уже отпадает необходимость в подсчете усилий N4 и Q4 , ибо последние не отличаются от соответствующих усилий в сечении 3:
N4 = 13, 56 кН,
Q4 = 1, 62 кН.
Сечение 5
ΣM5отс = 0 : M5 +11 · 2−12, 62 · 5, 5 = 0 →
M4 = 47, 43 кНм.
ΣPτотс = 0 : N5 + 11 − 12, 62 = 0 →
N5 = 1, 62 кН.
ΣPνотс = 0 :
Q5 + 13, 56 = 0 → Q5 = −13, 56 кН.
Следует обратить внимание на то, что изгибающие
моменты в сечениях 4 и 5 совпадают, тогда как поперечные и продольные силы «поменялись» местами.
Сечение 6
Так как в рассматриваемом сечении расположен шарнир, то изгибающий момент в нем отсутствует:
M6 = 0.
33
Задача 1
Продольная сила здесь остается такой же, что и в сечении 5; поперечная сила вычисляется обычным образом:
N6 = 1, 62 кН; ΣPνотс = : Q6 + 4, 5 + 13, 56 = 0 → Q6 = −18, 06 кН.
Сечение 7
ΣM7отс = 0: M7 + 4, 5 · 4, 5 +
+ 11 · 2 − 12, 62 · 5, 5 +
+ 13, 56 · 6 = 0 →
M7 = −54, 18 кНм.
Знак «минус» означает, что растянутыми являются верхние волокна стержня. Значения продольных и поперечных будут такими же, что и в сечении 6: N7 = 1, 62 кН, Q7 = −18, 06 кН.
Сечение 8
Для вычисления усилий в этом сечении можно воспользоваться способом вырезания узлов,
позволяющим выразить усилия в рассматриваемом сечении через уже найденные усилия в соседнем разрезе.
В данном случае от рамы отделяется узел,
находящийся между двумя смежными сечениями с номерами 7 и 8. В сечении 7, принадлежащему ригелю, показываются уже вычисленные усилия (с учетом их знаков), искомые усилия
N8 и Q8 изображаются положительными, изгибающий момент M8 направляется произвольно. Тогда
ΣM8отс = 0: M8 + 54, 18 = 0 → M8 = −54, 18 кНм;
ΣPτотс = 0: N8 + 18, 06 = 0 → N8 = −18, 06 кН;
ΣPνотс = 0: Q8 + 1, 62 = 0 → Q8 = −1, 62 кН.
34
Статически определимые конструкции
Сечение 9
Для определения усилий в этом сечении используется прием, который аналогичен только что описанному приему. Но на сей раз рассматривается равновесие не узла, а отделенного от рамы разрезами 8
и 9 вертикального стержня.
ΣM9отс = 0: M9 + 54, 18 + 1, 62 · 2 = 0 →
M9 = −57, 42 кНм;
ΣPτотс= 0: N9 +18, 06 = 0 → N9 = −18, 06 кН;
ΣPνотс = 0: Q9 + 1, 62 = 0 → Q9 = −1, 62 кН.
Сечение 10
В данном случае удобнее рассматривать равновесие нижней отсеченной части рамы, состоящей по
сути дела всего из одного стержня. Ясно, что к нему
приложено гораздо меньше как активных нагрузок
(только одна), так и реакций опорных связей, нежели к отброшенной части конструкции.
ΣM10отс = 0: M10 − 8, 75 · 1, 75+
+7, 13 · 3, 5 = 0 → M10 = −9, 62 кНм;
ΣPτотс = 0: N10 + 28, 69 = 0 →
N10 = −28, 69 кН;
ΣPνотс = 0: Q10 + 8, 75 − 7, 13 = 0 →
Q10 = −1, 62 кН.
Сечение 11
Здесь также рассматривается равновесие нижней отсеченной части
конструкции. Вычисления усилий в данном случае элементарны. Вот
результаты:
M11 = 0, N11 = −28, 69 кН, Q11 = 7, 13 кН.
35
Задача 1
Сечение 12
В этом сечении усилия целесообразно находить, рассматривая равновесие узла, выделенного сечениями 9, 10 и 12.
ΣM12отс = 0: M12 +57, 42−9, 62 = 0 → M12 = −47, 80 кНм;
ΣPτотс = 0: N12 − 1, 62+1, 62 = 0 → N12 = 0 кН;
ΣPνотс = 0: Q12 −28, 69+18, 06 = 0 → Q12 = 10, 63 кН.
Сечение 13
M13 = 0 (шарнир);
ΣPτотс = 0: N13 = 0;
ΣPνотс = 0: Q13 − 8 − 5, 25 + 2, 62 = 0 →
Q13 = 10, 63 кН.
Сечение 14
Рассматривается равновесие узла, выделенного сечениями 13 и 14:
M14 = 0 (шарнир); N14 = 0;
ΣPνотс = 0: Q14 = 10, 63−8 = 2, 63 кН.
Сечение 15
M15 = 0 (шарнир); N15 = 0; Q15 = −2, 63 кН.
На этом вычисление усилий в расчетных сечениях конструкции заканчивается.
Заключает расчет построение эпюр усилий
M , Q и N . Каждая из них изображается на осевом контуре конструкции по правилам, излагаемым на следующей странице. Ординаты эпюры
изгибающих моментов откладываются со стороны растянутых волокон каждого стержня. Эпюра поперечных сил изображается так, чтобы при
обходе каждого контура рамы по часовой стрелке скачки на диаграмме "Q" были направлены
36
Статически определимые конструкции
в сторону действия нагрузки. На стержне, принадлежащем двум контурам рамы, эпюра "Q" строится только при обходе одного из них.
Ординаты эпюры "N " независимо от знака продольной силы откладываются с любой стороны стержня. Однако знаки усилий N (так
же, как и знаки усилий Q) на соответствующих графиках проставляются обязательно, тогда как в указании знаков изгибающих моментов
на эпюре "M " необходимости нет. Следует также иметь в виду, что
там, где к конструкции приложена равномерно распределенная на-
Задача 1
37
грузка, эпюра "M " «выгнута» в сторону ее действия. При этом в том
месте, где поперечная сила равна нулю, эпюра "M " имеет экстремум.
Такой информации об эпюре изгибающих моментов достаточно, чтобы
довольно точно изобразить любой криволинейный участок диаграммы
"M " по двум ее крайним ординатам.
38
Статически определимые конструкции
Задача 2. Построение эпюр усилий в трехшарнирной арке
2.1. Общие сведения о трехшарнирных арках. Ниже рассматриваются симметричные трехшарнирные арки, к которым прикладывается
несимметричное вертикальное силовое воздействие. Опорные реакции
– вертикальные VA , VB и распор H арки – можно найти по расчетной
схеме конструкции следующим образом:
ΣMB = 0, → VA , ΣMA = 0 → VB , проверка: ΣY = 0;
ΣMCлев = 0 → H, ΣMCправ = 0 → H, проверка: ΣX = 0.
Для вычисления усилий составляются условия равновесия отсеченной части конструкции. В месте разреза изображаются (положительными) усилия: продольная сила N , растягивающая отсеченную часть
арки, поперечная сила Q, вращающая названную часть по часовой
стрелке, а также изгибающий момент M , который растягивает нижние волокна бруса. Тогда
P
P
P
Mk = 0 → M = M 0 − Hy,
Pνотс = 0 → Q = Q0 cos ϕ − H sin ϕ,
(2.1)
Pτотс = 0 → N = −Q0 sin ϕ − H cos ϕ.
В этих формулах M 0 = M 0 (x) – изгибающий момент в сечении k,
порожденный всеми вертикальными нагрузками, включающими и реакцию VA , которые приложены к левой отсеченной части конструкции,
а Q0 = Q0 (x) – проекция указанных сил на вертикальную ось, т. е. на
ось 0y. Усилия M 0 и Q0 называют балочными, так как точно такими
будут изгибающий момент и поперечная сила в балке, имеющей тот
же пролет l, что и арка, и воспринимающей ту же самую, что и арка,
вертикальную нагрузку.
39
Задача 2
Одинаковы в арке и описанной выше балке и реакции VA , VB , поэтому их тоже называют балочными. Однако в опорах арки, кроме
реакций VA и VB , возникают и горизонтальные реакции, именуемые
распором, что и нашло отражение в формулах (2.1). Из этих формул
видно также, что найти усилия можно лишь при заданной форме оси
конструкции, т. е. при известной функции y = y(x), описывающей эту
ось. Тогда по производной y ′ (x) ≡ tg ϕ однозначно находят величины
1
,
cos ϕ = q
1 + (y ′ )2
sin ϕ = y ′ cos ϕ,
(2.2)
нужные для вычисления поперечных и продольных сил.
Ниже рассматриваются три формы оси арки.
Параболическая
арка
4f
4f
x(l − x), y ′ = 2 (l − 2x).
2
l
l
С использованием обозначений
x
f
(0 ≤ ξ ≤ 1)
(2.3)
k= , ξ=
l
l
эти формулы можно представить в более удобном при вычислениях
виде:
y = 4klξ(1 − ξ), y ′ = 4k(1 − 2ξ).
y=
Для вычисления косинуса и синуса угла наклона касательной к оси
арки применяются формулы (2.2).
Синусоидальная
y = kl sin πξ,
арка
y ′ = kπ cos πξ.
Здесь также нужно опереться на зависимости (2.3) и (2.2).
40
Статически определимые конструкции
Круговая
арка
Чтобы описать ось арки, надо сначала по размерам l и f найти радиус дуги
окружности, по которой арка очерчена, и
указать формулы для синуса и косинуса
угла ϕ. Это делается при помощи геометрических рассмотрений с использованием
обозначений (2.3).
1 − 2ξ
1 + 4k 2
l, sin ϕ =
l, cos ϕ =
R=
8k
2R
q
1 − sin2 ϕ .
Тогда
kl
, y = R(cos ϕ − cos ϕ0 ).
R
Теперь можно перейти к рассмотрению примера расчета.
cos ϕ0 = 1 −
2.2. Расчетная схема. Вычерчивается по данным таблицы 1 (с. 10)
и рис. 11 (с. 27) согласно шифру 843. На расчетной схеме указываются
размеры конструкции, заданная нагрузка (равнодействующая распределенной нагрузки равна 18 кН) и реакции опор. При
l2 = 3 м, l3 = 3, 5 м, l4 = 4, 5 м, l5 = 2 м, q1 = 1, 5 кН/м, P2 = 11 кН
расчетная схема конструкции имеет вид, представленный на рис. a. Рядом (рис. b) изображена балка, служащая для построения эпюр усилий
M 0 и Q0 . Этой информации достаточно, чтобы определить опорные
реакции арки в последовательности, указанной на с. 38. Но сначала
следует привести формулы, которые описывают ось арки (кубическая
парабола):
41
Задача 2
f
f
x(3 − 4x2 /l2 ), y ′ = (3 − 12x2 /l2 ), 0 < x < l/2.
l
l
При f = 8 м, l = 26 м, k = f /l = 8/26 = 0, 3077 и обозначении ξ = x/l эти
формулы примут вид:
y=
y = 8ξ(3 − 4ξ 2 ),
y ′ = 0, 3077(3 − 12ξ 2 ),
0 ≤ ξ ≤ 0, 5.
(2.4)
Тогда (см. зависимости (2.2))
1
,
cos ϕ = p
1 + (y ′ )2
sin ϕ = y ′ cos ϕ.
2.3. Опорные реакции. Итак (см. рис. a),
X
MB = 0: VA · 26−33 · 17−18 · 15 = 0 → VA = 31, 96 кН;
X
MA = 0: VB · 26−33 · 9−18 · 11 = 0 → VB = 19, 04 кН;
проверка:
X
Y = 0: 31, 96−33−18+19, 04 ≡ 0.
Далее:
X
MCлев = 0: H · 8−31, 96 · 13−33 · 4−18 · 2 = 0 → H = 30, 94кН;
X
MCпр = 0 : H · 8−19, 04 · 13 = 0 → H = 30, 94кН.
Оба способа вычисления распора привели к одному и тому же результату, что свидетельствует о правильности вычислений.
2.4. Балочные усилия. Сначала строят эпюры балочных изгибающих моментов и поперечных сил (рис. b), а затем записывают выражения для функций M 0 (x) и Q0 (x) на каждом из участков, где такие выражения различны. Задача решается методом сечений, который
использовался выше при расчете рамы. Положительный изгибающий
момент растягивает нижние волокна балки, а положительная поперечная сила вращает любую из ее отсеченных частей по часовой стрелке.
Абсцисса x отсчитывается от левой опоры.
Участок 1: 0 ≤ x < 9 (левая отсеченная часть) –
M 0 (x) = 31, 96 · x,
Q0 (x) = 31, 96.
42
Статически определимые конструкции
Участок 2: 9 < x ≤ 13 (левая отсеченная часть) –
1
M 0 (x) = 31, 96x − 33(x − 9) − 4, 5(x − 9)2 ,
2
Q0 (x) = 31, 96 − 33 − 4, 5(x − 9).
Участок 3: 13 ≤ x ≤ 26 (правая отсеченная часть) –
M 0 (x) = 19, 04(26 − x),
Q0 (x) = −19, 04.
После приведения подобных членов и использования обозначения
x = ξ l = 26ξ можно следующим образом записать данные формулы:
M 0 (x) =

830, 96ξ при 0 ≤ ξ ≤ 0, 3462;



114, 75+1025, 7ξ −1521ξ 2 при 0, 3462 ≤ ξ ≤ 0, 5;



(2.5a)
495, 04(1 − ξ) при 0, 5 ≤ ξ ≤ 1.
Q0 (x) =

31, 96 при 0 ≤ ξ < 0, 3462;



39, 45 − 117ξ при 0, 3462 < ξ ≤ 0, 5;



(2.5b)
− 19, 04 при 0, 5 ≤ ξ ≤ 1.
2.5.Вычисление искомых усилий в расчетных сечениях. По формулам (2.1) видно, что для определения усилий в сечении с абсциссой x
необходимо знать геометрические параметры оси арки, даваемые формулами (2.4) и (2.2). Стало быть, требуются последовательные однотипные вычисления по формулам для усилий M 0 (x), Q0 (x), а также
по формулам (2.4), (2.2) и (2.1) при различных значениях аргумента x.
Такие вычисления удобно проводить в табличной форме. С этой целью
пролет арки разбивается на равные участки и в той последовательности, в которой располагаются столбцы таблицы, ведутся подсчеты
фигурирующих в расчетных формулах величин для каждого сечения
арки (каждого аргумента x или ξ, попадающего на точку деления).
Из сказанного следует, что число строк таблицы совпадает с числом
граничных точек участков разбиения. Таблица заполняется столбец за
столбцом с соблюдением следующих правил:
1. Формулы (2.4) описывают ось только левой половины арки, а
потому элементы столбцов 3–6 вычисляются по этим формулам и равенствам (2.2) лишь в верхней части таблицы, а элементы в ее нижней
Задача 2
43
половине записываются с учетом симметрии конструкции и того обстоятельства, что функции y(x) и cos ϕ четные, а функции y ′ (x) ≡ tg ϕ
и sin ϕ нечетные.
2. Балочные усилия M 0 (x) и Q0 (x) вычисляются по формулам
(2.5a) и (2.5b), приведенным на с. 42.
3. Искомые усилия в арке подсчитываются по формулам (2.1) при
найденном до этого значении распора. В данном случае H = 30, 94 кН.
В рассматриваемом примере пролет арки разбит на 16 равных
участков. Нумерация участков и узлов выполнена так, чтобы номера самого участка и его концевой точки совпадали (см. рис. на с. 45).
Табл. 2.1, заполненная по только что описанным правилам, приведена
на следующей странице.Значения усилий M , Q и N во всех расчетных
(пронумерованных) сечениях содержатся соответственно в 9-м, 13-м и
последнем столбцах таблицы. По этим значениям и построены все три
эпюры искомых усилий, которые изображены на с. 45, т. е. сразу же
за таблицей 2.1.
Следует обратить внимание на следующие обстоятельства. Во-первых, эпюры в арках изображаются не на осевой линии конструкции,
а на оси абсцисс, что гораздо удобнее. При этом, естественно, однозначное соответствие абсциссы сечения значению усилия сохраняется.
Правила знаков и правила построения те же, что и при изображении
эпюр в балках. Ординаты эпюры "M " откладываются со стороны растянутых волокон. В местах приложения сосредоточенных сил на этой
эпюре имеются переломы. Однако, в отличие от балочной эпюры, график функции M (x) имеет нелинейное очертание всюду, а не только в
местах приложения распределенной нагрузки. Объясняется это наличием слагаемого Hy в первой из формул (2.1).
Теперь о переломе на эпюре "M " в том месте, где приложена сила P = 33 кН. При помощи данных, содержащихся в таблице, его обнаружить не удастся, ибо названная сила не приложена ни в одной
из расчетных точек: она находится между сечениями 5 и 6. Поэтому при изображении эпюры "M " надо плавно продолжить левую (за
точку 5) и правую (за точку 6) ветви графика до их пересечения на
вертикали, вдоль которой приложена сила P , и тем самым обозначить
обсуждаемый перелом. Именно в этом месте изгибающий момент будет максимальным, так что его необходимо вычислить. Это нетрудно
сделать, ибо безразмерная абсцисса (ξ = 0, 3462), распор (H = 30, 94),
44
Статически определимые конструкции
балочный изгибающий момент (M 0 = 287, 64; см. рис. b на с. 40) известны. Тогда, согласно формулам (2.4)1 и (2.1)1 ,
y = 8ξ(3 − 4ξ 2 ) = 6, 981; M = M 0 −Hy = 287, 64−215, 99 = 71, 65.
45
Задача 2
На эпюре поперечных сил в месте приложения сосредоточенной силы P = 33 кН должен быть скачок, который можно обнаружить только
при продолжении соответствующих ветвей эпюры "Q" до линии действия силы P . Получающийся скачок силе P , как было бы в балке,
равняться не будет. Согласно второй из формул (2.1), он должен равняться величине P cos ϕ. При ξ = 0, 3462 формулы (2.4)2 и (2.2) дают:
y ′ = 0, 4805 , cos ϕ = 0, 9013 , sin ϕ = 0, 4331,
стало быть, ∆Q = P ·cos ϕ = 29, 74. С другой стороны (см. эпюру "Q0 "
46
Статически определимые конструкции
на стр. 40 и равенство (2.1)2 ),
Q|x=9−0 = Q0 cos ϕ − H sin ϕ =
= 31, 96 · 0, 9013 − 30, 94 · 0, 4331 = 15, 41,
Q|x=9+0 = Q0 cos ϕ − H sin ϕ =
= −1, 04 · 0, 9013 − 30, 94 · 0, 4331 = −14, 34.
И снова
∆Q = −Q|x=9−0 − Q|x=9+0 = 15, 41 − (−14, 34) = 29, 75.
После того, как эпюра "Q" будет построена, нужно убедиться в
том, что в тех точках, где поперечная сила меняет знак, изгибающие
моменты экстремальны.
Осталось отметить, что положительные ординаты эпюры поперечных сил откладываются сверху, а также предложить самостоятельно
выполнить вычисления и убедиться в том, что на эпюре "N " имеется
скачок |P sin ϕ| = 14, 29 в месте приложения сосредоточенной силы.
2.6. Использование электронных таблиц для вычисления усилий
в арке. Описанную выше процедуру получения усилий в арке удобно реализовать в среде Excel, которая в отличие от специальных программ расчета инженерных конструкций вполне доступна. Эта среда
позволяет создать таблицу с меньшим числом столбцов, нежели насчитывает табл. 2.1 со с. 44, поскольку целый ряд промежуточных
результатов фиксировать особой необходимости нет.
К заполнению электронной таблицы приступают после записи формул (2.4), характеризующих ось арки, и формул (2.5) для балочных
усилий. Число столбцов таблицы зависит от степени детализации промежуточных вычислений. Если свести такую детализацию к минимуму, то можно будет ограничиться всего 11 столбцами, в которых,
помимо номеров расчетных сечений (первый столбец), фиксируются
значения величин
ξ, y, y ′ ≡ tg ϕ, cos ϕ, sin ϕ, M 0 , Q0 , M, Q, N.
Число строк таблицы зависит от числа расчетных сечений (в выполненном примере их было 17) и от числа пролетных сосредоточенных сил. Для каждой такой силы надо зарезервировать две строки,
Задача 2
47
чтобы иметь возможности находить поперечную и продольную силу
по обе стороны от приложенного воздействия. Но первые места в таблице должны отводиться строкам, которые отвечают равноотстоящим
расчетным сечениям. Это объясняется тем, что таблица заполняется
последовательным вводом расчетных формул в первую строку каждого столбца с их дальнейшим копированием в остальные строки. Для
равноотстоящих сечений и для сечений, расположенных произвольным образом, такое копирование выполняется разными способами.
Копия электронной таблицы с результатами вычислений приведена на следующей странице. Первая строка таблицы отведена для общего заголовка. Она отделена тремя пустыми строками от строки 5,
содержащей заголовки столбцов таблицы. Эта информация вносится
в соответствующие клетки непосредственно с клавиатуры. Символ ξ,
входящий в заголовок второго столбца, вводится с помощью опции меню "Вставка/Символ". Каждому расчетному сечению соответствует
одна строка в таблице (основной раздел). Две последние строки отведены для обработки сечения, в котором приложена сосредоточенная
сила (дополнительный раздел).
Первый столбец таблицы заполнен номерами расчетных сечений
арки. Это целые числа от 0 до 16. Второй столбец содержит значения
безразмерных координат ξ указанных сечений. В клетку B5 внесена формула =A5/16, которая затем копировалась во все клетки основного раздела данного столбца. В клетки дополнительного раздела
(B22:B23) введено число =0,3462, т. е. значение безразмерной координаты ξ сечения, в котором прикладывается сосредоточенная сила. И
далее при комментировании выполняемых операций набор символов,
вносимых с клавиатуры в то или иное поле таблицы, будет выделяться
синим цветом.
В первые клетки столбцов 3–6 таблицы, содержащих значения координаты y, тангенса, косинуса и синуса угла наклона касательной
к оси арки, т. е. в ячейки C5–F5, последовательно записаны формулы: =8*B5*(3-4*B5*B5) , =0,3077*(3-12*B5*B5) , =1/(1+D5*D5)ˆ 0,5
и =D5*E5. Затем эти формулы, выделенные в блок, копируются до
13 строки, соответствующей центральному шарниру, т. е. для всех сечений левой половины арки. Данные для правой половины арки получают с учетом симметрии конструкции и четности функций. Для
этого в клетки четырнадцатой строки вводятся, а затем копируются во
48
Статически определимые конструкции
все последующие строки основного раздела числа, характеризующие
четность функций: в клетки столбцов C и E – число 1, а в столбцы D и
F – число -1. Далее поля C5:F12, содержащие уже подсчитанные гео-
Задача 2
49
метрические характеристики для левой половины арки, выделяются в
единый блок и копируются в клетки, соответствующие сечениям правой части конструкции (в клетки C14:F21). Это делается с помощью
пункта меню "Правка/Специальная вставка/значения/умножить".
Наконец, величины, находящиеся в выделенном на предыдущем этапе работы с таблицей блоке (ячейки C14:F21), перераспределяются с
помощью пункта меню "Данные/Сортировка по убыванию".
В клетки дополнительного раздела из верхней части таблицы обычным образом копируются нужные формулы для подсчета геометрических характеристик сечения, к которому приложена сосредоточенная
сила. Здесь важно помнить о том, что при переходе от левой части
конструкции к правой синусы и тангенсы меняют знак на обратный.
Признаком правильности выполненных действий служат следующие
значения величин в замковом сечении арки: тангенс и синус угла наклона касательной равны нулю, косинус этого же угла равен единице,
а ордината y равна стреле f .
В столбцы G и H таблицы вносятся формулы (2.5a) и (2.5b) для
подсчета балочных усилий в расчетных сечениях. В каждую строку,
отвечающую началу участка (всего ось балки разбита на три участка), записывается нужная формула, которая затем копируется во все
остальные строки данного участка. В клетки дополнительного раздела копируются формулы для балочных усилий, отвечающие тому
участку, на котором приложена сосредоточенная сила. В последние
три столбца таблицы помещаются формулы (2.1) для искомых усилий
(см. с. 38). Они копируются во все строки основного и дополнительного диапазонов таблицы. В результате в строчках основного раздела
будут содержаться данные для построения эпюр усилий, а в строчках
дополнительного диапазона – данные для правильного изображения
перелома на эпюре M и скачков на эпюрах Q и N .
При построении графиков найденных усилий надо иметь в виду,
что по умолчанию ось 0y направлена вверх, а потому эпюра изгибающих моментов будет отложена со стороны сжатых волокон. Чтобы избежать такого эффекта, можно добавить к таблице еще один столбец,
в котором дублируются (копируются) значения изгибающих моментов
с обратным знаком. Данные для построения графика берутся именно
из этого дополнительного столбца.
50
Статически определимые конструкции
Задача 3. Расчет составной балки с учетом действия
временной нагрузки
Текст задания приведен на с. 11–13. Схема конструкции изображена на рис. 11.
3.1. Предварительные замечания. Перед выполнением задания следует по какому-либо из литературных источников ознакомиться с кинематическим способом построения линий влияния и правилами их
использования. В пособии [1] необходимая информация о работе с линиями влияния содержатся на с. 423–436.
Порядок построения линий влияния (л. в.) изгибающих моментов
в балках таков.
1. В соответствующее сечение балки вводится шарнир и форма
линии влияния, т. е. модель (м. л. в.) устанавливается как картина
возможных перемещений получившегося механизма.
2. Над одной из характерных ординат модели линии влияния, т. е.
там, где на графике имеется перелом, размещается единичная сила и
по формуле
mi = −uP /Ui
определяется значение этой ординаты. Здесь uP – вертикальное перемещение точки приложения единичной
силы, которое берется положительным, если направления силы и перемещения совпадают; Ui – перемещение, сопряженное с усилием Mi .
Этот угол положителен, если обе его составляющие (αi и βi ) имеют те
же направления, что и моменты Mi , прикладываемые по обе стороны
от введенного шарнира так, чтобы были растянуты нижние волокна.
3. Из геометрических соображений (подобие треугольников) находят остальные характерные ординаты линии влияния.
Сказанное поясняет пример построения линий влияния усилий M1
и M2 в балке, изображенной на следующей странице (рис. a).
Построение л. в. M1 начинается с постановки в сечении 1 шарнира, после чего получившемуся механизму придается возможное перемещение. В результате сместившиеся звенья механизма укажут на
51
Задача 3
конфигурацию модели линии влияния усилия M1 . Эта конфигурация
отображена на рис. b жирной линией. Так как
y y
yl
uP = y, U1 = −α1 −β1 = − − = − ,
a b
ab
то
m1 = −
ab
y(−ab)
uP
= .
=−
U1
yl
l
Искомая линия влияния дана на нижнем из рисунков b. Ее крайнюю левую
ординату bc/l находят из подобия треугольников. При изображении любой
линии влияния положительные ординаты откладываются ниже оси абсцисс.
На рис. c приведена модель линии
влияния изгибающего момента M2 . Она
является следствием постановки в сечении 2 шарнира и последующим за этим
возможным перемещением образовавшегося механизма. В данном случае
uP = y, U2 = α2 =
y
uP
yc
, m2 = −
= − = −c.
c
U2
y
Линия влияния усилия M2 дана на нижнем из рисунков c.
Таким образом, в балках встречаются два типа линий влияния изгибающих моментов.
Линия влияния типа 1. Смещаются диски по обе стороны от введенного шарнира (рис. b). В этом случае ордината линии влияния в
точке, где был поставлен шарнир, определяется по формуле m = ab/l.
Линия влияния типа 2. Смещается только один из дисков, примыкающих к введенному шарниру (рис. c). Тогда ближайшая из характерных ординат к данному шарниру определяется формулой m = −c.
3.2. Расчетная схема. Вычерчивается по данным табл. 2 (с. 13) и
рис. 11 (с. 27), отвечающим шифру 843.
52
Статически определимые конструкции
3.3. Линии влияния изгибающих моментов. Строятся для всех семи расчетных сечений, указанных на схеме балки, по правилам, изложенным в п. 3.1. Результаты построения приведены ниже. Рядом с
каждым графиком указываются значения ω + и ω − площадей положительных и отрицательных участков линии влияния (в м2 ).
53
Задача 3
3.4. Огибающая эпюра изгибающих моментов. Наибольшие и наименьшие значения изгибающего момента в сечении i балки определяются формулами
max Mi = MiC + ωi+ p и min Mi = MiC − ωi− p,
в которых через MiC обозначен изгибающий момент от постоянной нагрузки, а через p – интенсивность временной нагрузки. Для определения MiC следует воспользоваться соотношением
MiC = P yi + qωiC + T tg αi ,
где P , q, T – значения воздействий, указанных на расчетной схеме балки, yi – ордината л. в. Mi в точке приложения силы P , ωiC – площадь
л. в. Mi на участке расположения равномерно распределенной нагрузки интенсивностью q, tg αi – тангенс угла наклона л. в. Mi на участке
загружения балки сосредоточенным моментом T .
Последующие вычисления ведутся с учетом того, что P = 12 кН,
T = 11 кНм, q = 3, 5 кН/м, p = 4 кН/м.
Сечение 1
M1 = 12 · (−0, 6) = −7, 2 кНм;
C
max M1 = −7, 2 + 0 · 4 = −7, 2 кНм;
min M1 = −7, 2 − 0, 18 · 4 = −7, 92 кНм.
Далее размерность усилий не указывается.
Сечение 2
M2C = 12 · (−0, 3) + 0, 5 · 7 · (−2, 25) · 3, 5 = −31, 16;
max M2 = −31, 16 + 4, 5 · 4 = −13, 16;
min M2 = −31, 16 − 13, 03 · 4 = −83, 28.
Сечение 3
C
M3 = 0, 5 · 7 · (−4, 5) · 3, 5 = −55, 12;
max M3 = −55, 12;
min M3 = −55, 12 − 25, 88 · 4 = −158, 64.
Сечение 4
C
M4 = 0, 5 · 7 · 1, 75 · 3, 5 = 21, 44;
max M4 = 21, 44 + 6, 12 · 4 = 45, 92;
min M4 = 21, 44.
54
Статически определимые конструкции
Сечение 5
C
M5 = −25, 88 · 3, 5 = −90, 58;
max M5 = −90, 58;
min M5 = −90, 58 − 25, 88 · 4 = −194, 10.
Сечение 6
Здесь приложен сосредоточенный момент T , поэтому находят два
значения усилия M6 : слева и справа от данного сечения.
Сечение 6 − 0. Расположено чуть левее точки 6, поэтому воздействие T оказывается справа от точки A, показанной на л. в. M6 , т. е.
сосредоточенный момент T прикладывается на участке, для которого
tg α6 = 0. Стало быть,
C
= (22, 66 − 0, 5 · 4 · 3, 5) · 3, 5 = 54, 81;
M6−0
max M6−0 = 54, 81 + 22, 66 · 4 = 145, 45;
min M6−0 = 54, 81 − 13, 12 · 4 = 2, 33.
Сечение 6 + 0. Теперь воздействие T оказывается приложенным
слева от точки A. Если данное воздействие представить в виде пары
сил, то можно будет увидеть, что знак произведения T tg α6 определяется левой силой, поскольку она приложена в точке, где модуль ординаты л. в. M6 больше. Сила, направленная вниз, положительна, а так
как ордината, соответствующая этой силе, отрицательна, то отрицательным будет и произведение T tg α6 .
Итак,
C
C
− 11 ·
= M6−0
M6+0
3, 5
= 43, 81.
3, 5
Следовательно, max M6+0 = 43, 81+22, 64 · 4 = = 134, 45;
min M6+0 = 43, 81−13, 12 · 4 = −8, 67.
Сечение 7
C
M7 = (45, 31 − 0, 5 · 7 · 4) · 3, 5 − 11 · (7/7) = 98, 58;
max M7 = 98, 58 + 45, 31 · 4 = 279, 82;
min M7 = 98, 58 − 38, 5 · 4 = −55, 42.
Ординаты max Mi , min Mi откладываются от оси абсцисс и нанесенные точки соединяются плавными линиями. Получающаяся в ре-
Задача 3
55
зультате таких операций огибающая эпюра изгибающих моментов приведена ниже. При изображении огибающей учитывается, что в шарнирах и на свободном конце консоли изгибающие моменты отсутствуют.
На тех участках эпюры, где величины max Mi и min Mi имеют одинаковый знак, меньшие по модулю усилия изображены штриховыми
линиями. На огибающей, как и на обычной эпюре изгибающих моментов, в местах действия сосредоточенных сил имеются переломы, соответствующие направлениям этих сил, а там, где приложены сосредоточенные моменты, наблюдаются скачки, равные значениям моментных воздействий. Можно обратить внимание и на то, что огибающая
эпюра имеет искривленные участки и там, где равномерно распределенная постоянная нагрузка отсутствует. Объясняется это тем, что на
этом участке в своем опасном положении оказывается расположенной
равномерно распределенная временная нагрузка.
3.5. Линии влияния поперечных сил. Строятся для поперечных
сил в сечениях 2 и 5, отмеченных на расчетной схеме
балки штрихом (см. с. 52), кинематическим способом.
При этом для усилия Q5 имеются две линии влияния:
слева и справа от опоры. Модели линий влияния получают, вводя в соответствующие сечения специальные
шарниры, состоящие из двух параллельных стержней.
56
Статически определимые конструкции
Относительные перемещения соединенных таким шарниром дисков
могут быть только поступательными. Построенные указанным образом линии влияния приводятся ниже.
При помощи данных линий влияния подсчитываются значения поперечных сил от постоянной нагрузки:
QC2 = 12 · 0, 1 − 0, 5 · 7 · 0, 75 · 3, 5 = −7, 99 кН,
QC5−0 = −(0, 5 · 7 · 1 + 1 · 4, 5) · 3, 5 = −28 кН,
QC5+0 = [0, 5 · 1, 125 · (7 + 4, 5) + 0, 5 · 1 · 4] · 3, 5 = 29, 64 кН.
57
Задача 4
Задача 4. Расчет плоской фермы с учетом
временной нагрузки
4.1. Предварительные замечания. Текст задания приведен на с. 13–
14, схема конструкции дана на рис. 11. Перед решением задачи способом, знакомым еще по курсу теоретической механики, полезно ознакомиться с современными методами расчета ферм на постоянную и
временную нагрузки. В пособии [1] указанный материал содержится
на с. 384–392.
4.2. Расчетная схема. Вычерчивается по рис. 11 (см. с. 27) с использованием шифра 843 и табл. 3, помещенной на с. 13. Временная равномерно распределенная нагрузка интенсивности p может занимать
любое положение на нижнем поясе фермы, что и было учтено при ее
изображении.
4.3. Расчет на постоянную нагрузку. Выполняется методом сечений. Предварительно узлы фермы нумеруются и в них сводится равномерно распределенная нагрузка. Делается это так, как показано на
рисунках, расположенных ниже. Нагрузка, находящаяся на нижнем
поясе, приводится только к промежуточным узлам.
58
Статически определимые конструкции
Узловые силы рассчитываемой конструкции таковы (см. приводимый ниже рисунок): P = qd = 5, 5 кН/м · 3, 5 м = 19, 25 кН. Тогда
RA = RB = 0, 5 · 5P = 48, 125 кН.
Размер c = 1, 4 м установлен из подобия треугольников:
8, 5
c + 10, 5
=
.
c+7
6
Далее используется теорема Пифагора и тот факт, что косинус угла
равен отношению прилегающего катета к гипотенузе соответствующего прямоугольного треугольника:
6
= 0, 8638,
cos α1 = q
62 +3, 52
sin α1 = 0, 5039;
8, 5
= 0, 9247,
cos α2 = q
8, 52 +3, 52
sin α2 = 0, 3807;
3, 5
cos α3 = q
= 0, 8137,
3, 52 +2, 52
sin α3 = 0, 5812.
Теперь можно перейти к определению усилий. Из-за симметрии
задачи следует ограничиться нахождением продольных сил только в
59
Задача 4
стержнях левой половины фермы.
С е ч е н и е I–I
P
P
M2лев = 0: N8−9 · 6 + 48, 125 · 3, 5 = 0 → N8−9 = −28, 0729 кН;
P
M8лев = 0: N1−2 · 6 = 0 → N1−2 = 0;
Y лев = 0: −N2−8 · 0, 8638 + 48, 125 = 0 → N2−8 = 55, 7145 кН.
Далее размерность усилий не указывается.
С е ч е н и е II – II
P
P
P
M3лев
= 0: N9−10 · 6 + 48, 125 · 7 − 19, 25 · 3, 5 = 0 →
N9−10 = −44, 9167;
M9лев = 0: N2−3 · 6 − 48, 125 · 3, 5 = 0 → N2−3 = 28, 0729;
Y лев = 0: − N3−9 · 0, 8638 + 48, 125 − 19, 25 = 0 → N3−9 = 33, 4287.
С е ч е н и е III – III
При составлении уравнения равноP
весия M3лев = 0 усилие N10−11 удобно разложить на две составляющие
так, как это показано на рисунке:
H
N10−11
· 6+48, 125 · 7−19, 25 · 3, 5 =
H
= −44, 9167.
= 0 → N10−11
Следовательно,
H
/ cos α3 = −44, 92/0, 8137 = −55, 1983.
N10−11 = N10−11
Далее:
P
лев = 0: N
M11
3−4 · 8, 5 − 48, 125 · 10, 5 + 19, 25 · 3, 5 = 0 →
N3−4 = 35, 6691;
P
MCлев = 0:
V
N3−11 · 8, 4+48, 125 ·1, 4−19, 25 · 4, 9−
V
−19, 25 · 8, 4 = 0 → N3−11
= 22, 4583.
Тогда
V
/ cos α2 = 22, 4583/0, 9247 = 24, 2877.
N3−11 = N3−11
60
Статически определимые конструкции
С е ч е н и е IV – IV
P
Y
лев
= 0: N2−9 + 48, 125 − 19, 25 = 0 → N2−9 = −28, 8750.
Усилия в остальных стержнях определяются способом вырезания
узлов. От фермы последовательно отделяются узлы 1, 4, 10, и условия
их равновесия составляются таким образом, чтобы каждое уравнение
более одной неизвестной величины не содержало. Все необходимые вычисления имеются на приводимых ниже рисунках.
4.4. Построение линий влияния. Расчетные усилия. Линии влияния усилий в ферме предлагается построить смешанным способом, а
именно: найти сначала модели линий влияния продольных сил во всех
неопорных стержнях конструкции, а затем аналитически определить
масштаб и знак построения.
Как уже отмечалось при решении задачи 3, для построения модели линии влияния некоторого усилия в статически определимой конструкции, надо удалить связь, воспринимающую это усилие, и установить очертание (модель) искомой линии влияния как картину возможных перемещением получившегося механизма. Именно такой способ
действий и называют кинематическим.
В верхней части рисунка, помещенного на следующей странице,
изображена рассчитываемая ферма, ряд стержней которой пронумерован (учитывается симметрия). На нижнем поясе фермы в произвольном месте указывается единичная сила, чтобы подчеркнуть роль
этого пояса как грузового. Под расчетной схемой конструкции расположены эскизы, иллюстрирующие процедуру построения моделей
линий влияния. На каждом эскизе представлена дисковая модель фермы, которая получается после удаления в конструкции стержня с таким же номером, что и номер эскиза. По обе стороны от удаленного
Задача 4
61
стержня образуются неизменяемые конфигурации стержней, которые
объединяются в диски 1 и 2.
Если удалить в конструкции стержень 1, то останется один диск,
присоединенный к земле двумя параллельными стержнями. Этот диск
62
Статически определимые конструкции
по вертикали (т. е. по направлению единичной силы) перемещаться не
может, а потому усилий в стержне 1 при любой вертикальной нагрузке не будет. Другими словами, если нет возможных перемещений по
вертикали, то нет и линии влияния усилия N1 .
Иначе обстоит дело при удалении стержня 2. Теперь образуются центры вращения двух дисков как относительно земли (шарниры,
выделенные синим цветом), так и относительно друг друга (шарнир,
окрашенный в красный цвет). Возможное положение загружаемого пояса диска 1 после поворота последнего относительно земли изображено на эскизе 2 тонкой синей линией (1), а возможное новое положение
грузового пояса диска 2 – линией (2)1 . Пересекаться же линии (1) и
(2) должны в том месте, где диски 1 и 2 не могут отделиться друг от
друга, т. е. под шарниром, отмеченным красным цветом. Остается на
прямых (1) и (2) выделить отрезки, которые отвечают габаритам конструкции. Эти отрезки изображены на эскизе утолщенными. Вместе с
тонкой горизонтальной прямой они и образуют искомую модель линии
влияния продольной силы в стержне 2, обозначаемую как м. л. в. N2 .
На полученной модели изображены также сила P = 1 и ордината y,
отнесенные к середине пролета фермы. Это говорит о том, что именно
ординату y намечается далее вычислить с тем, чтобы установить знак
и масштаб построения.
Совершенно аналогично строятся модели линий влияния усилий
N3 –N6 , что видно по эскизам 3–6 на приведенном выше рисунке.
Теперь внимание надо сосредоточить на рисунке, расположенном
на следующей странице. После удаления стержня 7 (эскиз 7) ферма
разбивается на два диска, возможные перемещения которых, как и
прежде, моделируются прямыми (1) и (2). Но дальнейшие действия
зависят от того, по какому поясу – нижнему или верхнему – перемещается единичная сила. Так, если грузовым является нижний пояс,
то сила по диску 1 может перемещаться только от точки F до точки A, поэтому именно эти точки и ограничивают тот отрезок F A на
прямой (1), который входит в состав искомой м. л. в. N7 . Аналогично,
на линии (2) в состав м. л. в. N7 отбирается только отрезок AB. На
построенной по указанным правилам модели линии влияния делается
надпись «Езда снизу», четко определяющая ее статус. Если же сила
1
Далее ради краткости будет говориться о новом положении диска, а не его
грузового пояса.
Задача 4
63
перемещается по верхнему поясу фермы, то на диск 1 она (сила) попасть не сможет, поэтому м. л. в. N7 включает в себя только отрезок
DE прямой (2).
Практически то же самое можно сказать и о м. л. в. N8 , только теперь надо обратить внимание на то, что диски 1 и 2 соединены
параллельными стержнями, а потому линии (1) и (2), моделирующие
возможные перемещения этих дисков, параллельны (см. задачу 3). Это
и показано на эскизе 8. Только что сказанное позволяет эскизы 11 и 12
64
Статически определимые конструкции
оставить без комментариев. Разве что можно отметить, что интервал
между дисками 1 и 2 на м. л. в. N12 заполняется соединительной прямой ab. Что же касается м. л. в. N13 , то тут надо иметь в виду, что
точка пересечения прямых, связывающих диски 1 и 2, исполняет роль
шарнира A между этими дисками, а потому линии (1) и (2) должны
пересекаться именно под этой точкой.
Нетрудно было заметить, что о моделях линий влияния усилий N9
и N10 выше ничего не говорилось. Это не случайно, ибо стержни 9
и 10 – особые. Через каждый из этих элементов нельзя провести разрез, который бы при разделении фермы на две части не затрагивал
бы еще минимум три других стержня. Для построения линий влияния усилий в стержнях такого рода кинематический способ не удобен.
Однако если предварительно получить линии влияния усилий во всех
остальных стержнях фермы, то возникшее затруднение удастся сравнительно легко преодолеть. В дальнейшем это и будет сделано.
Линия влияния отличается от своей модели только тем, что на
ней проставлены значения и знаки характерных ординат. Ясно, что
сначала достаточно установить лишь одну характерную ординату ломаной с тем, чтобы все остальные нужные для расчета конструкции
ординаты получать уже из подобия треугольников. Выше уже говорилось, что в первую очередь предполагается вычислять ординаты,
обозначенные на моделях линий влияния через y. По своему смыслу
ордината y на л. в. Ni равна усилию Ni в том случае, если единичная
сила находится в узле фермы, который расположен над этой ординатой. В рассматриваемой задаче величина y равна усилию Ni при
расположении единичной силы в середине нижнего пояса фермы (см.
эскизы на двух последних рисунках). Следовательно, достаточно расположить силу P = 1 в только что указанном месте и найти усилия во
всех стержнях левой половины конструкции, чтобы определить знаки
и значения центральных ординат всех линий влияния.
Расчет фермы на силу P = 1 можно выполнить методом сечений,
т. е. точно так же, как был выполнен расчет конструкции на постоянную нагрузку. Но так как последний уже сыграл назначенную ему
роль – дать представление о том, как при вычислениях вручную следует находить усилия в статически определимых фермах, то теперь
для отыскания усилий от воздействия P = 1 можно воспользоваться
любой специальной программой. В данном случае расчет выполнялся
Задача 4
65
при помощи программы ФЕРМА, о которой упоминалось на с. 6. Результаты расчета представлены на приведенных ниже линиях влияния
в виде значений ординат последних в середине пролета фермы.
66
Статически определимые конструкции
Остается построить линии влияния продольных сил N9 и N10 . Указанные усилия целесообразно находить методом вырезания узлов, что
и было сделано при расчете фермы на постоянную нагрузку. Так, при
вычислении продольной силы N9 вырезался узел 10 и составлялось
условие равновесия (см. рисунок на с. 60) N3−10 −N10−11 sin α3 = 0, из
которого при N3−10 ≡ N9 и N10−11 ≡ N6 следует, что N9 = N6 · sin α3 .
График левой части этого равенства такой же, как и у правой, т. е.
л. в. N9 = 0, 5812 л. в. N6 .
(4.1)
Стало быть, ординаты л. в. N9 отличаются от ординат л. в. N6 лишь
множителем 0,5812.
Сказанное относится к случаю, когда нагрузка находится на нижнем поясе конструкции. Именно так обстоит дело в рассматриваемом
примере. Но и при расположении единичной силы сверху формула
(4.1) будет справедлива до тех пор, пока эта сила находится слева от
узла 9 или справа от узла 11. Ситуация меняется, если сила P = 1
окажется между этими узлами. Так, при ее расположении в узле 10
равенство (4.1) придется заменить на соотношение
л. в. N9 = 0, 5812 л. в. N6 − 1,
что приводит к соответствующей корректировке характерной ординаты линии влияния.
Аналогично получена линия влияния усилия N10 , которое находят,
рассматривая равновесное состояние нижнего центрального узла фермы (узла 4; см. рисунок на с. 60). Если нагрузка приложена к верхнему
поясу, то N10 ≡ 0, но N10 = 0 и при расположении единичной силы на
67
Задача 4
нижнем поясе фермы за пределами двух ее центральных панелей. Если же эта сила находится в самом узле 4, то N10 = 1.
Расчетные усилия в ферме определяются формулами
max Ni = (ωi+ −ωi− )q+ωi+ p, min Ni = (ωi+ −ωi− )q−ωi− p,
(4.2)
которые полностью аналогичны соотношениям, использованным при
вычислении наибольших и наименьших значений изгибающих моментов в расчетных сечениях многопролетной балки (задача 3). Только
теперь в состав постоянной нагрузки не входят сосредоточенные силы и сосредоточенные моменты, а имеется лишь равномерно распределенное по нижнему поясу воздействие, что упрощает вычисления.
При этом заменять такое воздействие сосредоточенными силами, что
делалось при расчете фермы методом сечений, нет никакой необходимости. В рассматриваемой задаче q = 5, 5 кН/м, p = 3 кН/м. Результаты
вычислений по формулам (4.2) сведены в табл. 4.1.
Таблица 4.1
Номера
стержней
1 (1−2)
2 (2−3)
3 (3−4)
4 (8−9)
5 (9−10)
6 (10−11)
7 (1−8)
8 (2−9)
9 (3−10)
10 (4−11)
11 (2−8)
12 (3−9)
13 (3−11)
ωi+
ωi−
–
–
5,104
–
6,484
–
–
5,104
–
8,165
–
10,04
–
8,75
0,350 5,60
–
5,834
3,5
–
10,13
–
6,485 0,4053
4,903 0,4865
q(ωi+ −ωi− )
кН
max Ni
кН
min Ni
кН
0
28,07
35,66
-28,07
-44,91
-55,22
-48,12
-28,88
-32,09
19,25
55,72
33,44
24,29
0
43,38
55,11
-28,07
-44,91
-55,22
-48,12
-27,82
-32,09
29,75
86,10
52,89
39,00
0
28,07
35,66
-43,38
-69,40
-85,34
-74,38
-45,68
-49,59
19,25
55,72
32,22
22,83
Следует обратить внимание на то, что в четвертом столбце таблицы содержатся усилия NiC = q(ωi+ −ωi− ), вызванные действием только
постоянной нагрузки, и что они совпадают с продольными силами,
найденными в п. 4.3 методом сечений.
68
Статически определимые конструкции
Задача 5. Определение перемещений в плоской раме
Условие задачи приводится на с. 15.
5.1. Предварительные замечания. Перед выполнением работы следует изучить раздел «Вычисление перемещений в стержневых конструкциях от силового воздействия». Это можно сделать по любому
литературному источнику (учебнику, учебному пособию). В частности,
требуемый материал изложен на с. 277–286 книги [1]. Особое внимание
следует обратить на п. 9.7.
Перемещение UA сечения A конструкции, которая состоит из призматических стержней, вычисляется по формуле
UA = (M, M A ) =
C
X
ωj mAj
j=1
EIj
,
(5.1)
где M – изгибающие моменты от заданной нагрузки, M A – изгибающие
момент от единичного воздействия, прикладываемого по направлению
искомого перемещения, ωj – площадь эпюры "M " на участке осевого
контура с номером j, mAj – ордината эпюры "M A ", отвечающая положению центра тяжести эпюры "M " на участке j осевого контура (т. е.
ордината на графике "M A " , найденная в точке с абсциссой центра
тяжести фигуры "M ").
При вычислениях осевой контур конструкции разбивается на C
участков так, чтобы в пределах каждого из них усилие M A (или M ) менялось по линейному закону, а жесткость EIj была постоянной. Очень
важно следить за тем, чтобы ордината, соответствующая центру тяжести фигуры, площадь которой подсчитана, бралась на линейной эпюре. Эпюра "M A " всегда имеет кусочно-линейное очертание, тогда как
зависимость усилия M от координаты точки осевого контура может
быть и нелинейной. Поэтому в формуле (5.1) и предлагается подсчитывать площади участков эпюры "M ", а соответствующие их центрам
тяжести ординаты mAj брать на эпюре "M A ". Если же обе эпюры линейны, то на какой из них вычислять площади участков, а на какой
брать ординаты, безразлично.
Значения площадей и абсциссы центров тяжести наиболее распространенных эпюр приводятся в таблице 5.1. Более сложные фигуры
разбиваются на простые.
69
Задача 5
Порядок вычислений по формуле (5.1) таков:
– строится эпюра "M " от заданной нагрузки;
– по направлению искомого перемещения прикладывается воздействие PA = 1 и строится обусловленная этим воздействием эпюра изгибающих моментов "M A ";
– осевой контур конструкции разбивается на C прямолинейных
участков постоянной жесткости так, чтобы на каждом из них эпюра
изгибающих моментов "M A " была линейной;
– выполняются вычисления по формуле (5.1).
5.2. Расчетная схема. Рама, в которой требуется определить перемещения, рассматривалась при решении задачи 1. Но теперь на прежней расчетной схеме (см. с. 28) надо дополнительно указать изгибные
жесткости стержней. Для этого используются данные табл. 4, приведенной на с. 15. Так как (последняя цифра шифра 3)
ρ = EIc /EIp = 1/3,
то принимается EIc = EI, EIp = 3EI.
По заданию требуется найти горизонтальное и вертикальное перемещения одного из междисковых шарниров (по выбору студента),
а также угол поворота сечения, в котором приложена сила P2 . Ниже
вычисляются:
– вертикальное перемещение сечения B;
– горизонтальное перемещение сечения B;
– угол поворота сечения C.
70
Статически определимые конструкции
Все три перемещения вызываются постоянной нагрузкой. Эпюра
изгибающих моментов от этой нагрузки была получена при решении
задачи 1 (см. с. 36). Ниже она приводится повторно.
5.3. Вертикальное перемещение сечения B. Вычисления выполняются в последовательности, указанной в п. 5.1. Эпюра "M " уже имеется, так что следует заняться построV
ением эпюры "M B ". В точке B прикладывается вертикальная единичная
сила и определяются вызванные ею реакции опор.
X
MBпр = 0: R5 = 0;
X
X
X
ME = 0: R4 · 6−1 · 10, 5 = 0 → R4 = 1, 75;
MK = 0: R2 · 6 + 1 · 4, 5 = 0 → R2 = −0, 75;
MAлев = 0: R1 · 5, 5 − R2 · 3 = 0 → R1 = −0, 409;
71
Задача 5
X
MAпр = 0: R3 · 5, 5 − R4 · 3 + 1 · 7, 5 = 0 → R3 = −0, 409.
Правильность проделанных вычислений подтверждается следующими проверками:
X
X
X = 0: R1 − R3 = 0 → −0, 409 + 0, 409 ≡ 0;
Y = 0: 1 − R2 − R4 = 0 → 1 + 0, 75 − 1, 75 ≡ 0.
V
Эпюра "M B ", построенная по правилам, о которых шла речь при
решении задачи 1, приводится ниже. Рядом с ней указано разбиение осевого контура конструкции на участки. Это разбиение выполнено так, чтобы в пределах каждого пронумерованного участка эпюра
V
"M B " была очерчена по прямой линии.
При выполнении вычислений по формуле (5.1) прежде всего устанавливается знак. Он берется положительным, если обе эпюры (в расV
сматриваемом случае это эпюры "M " и "M B ") расположены на данном участке с одной стороны от линии осевого контура. Затем записывается податливость стержня, т. е. величина 1/EIj , обратная к изгибной жесткости. После этого подсчитывается площадь ωj нелинейной
V
эпюры и, наконец, берется ордината mBj
, отвечающая центру тяжести
площади ωj .
Остается реализовать только что описанную вычислительную процедуру. Она выполняется при помощи рисунков, приведенных на следующей странице.
Участок
UBV1 =
1
73, 71
1
·
· 3, 5 · 44, 18 ·
· 1, 43 =
.
EI
2
3
EI
1
2
72
Статически определимые конструкции
Участок
1
·
EI
2
1
· 2, 25 +
2
3
3
2
i
1
1
169, 01
· 2, 25 + · 1, 43 =
.
+ · 2 · 47, 43 ·
2
3
3
EI
UBV2 =
h 1
2
· 2 · 44, 18 ·
· 1, 43 +
Участок
3
1
·
· 47, 43 · 3 ·
· 2, 25 +
3EI
2
3
2 1, 5 · 32
1
i
36, 84
+ ·
·3 ·
· 2, 25 =
.
3
8
2
EI
h 1
UBV3 =
2
Участок
UBV4 =
4
40, 64
1
·
· 54, 18 · 3 ·
· 2, 25 =
.
3EI
2
3
EI
1
2
73
Задача 5
Участок 5
Здесь можно воспользоваться формулой для перемножения трапеций, приведенной, например, в пособии [1, с. 231].
UBV5 =
2
[2 · 54, 18 · 2, 25 + 2 · 57, 42 · 3, 07 + 54, 18 · 3, 07+
6EI
297, 30
.
+ 57, 42 · 2, 25] =
EI
Участок
UBV6 = −
1 h 1
6
2
· 9, 62 · 3, 5 ·
· 1, 43 +
EI 2
3
1
i
2, 5 · 3, 52
22, 44
· 3, 5 ·
· 1, 43 = −
.
+ ·
3
8
2
EI
Участок
7
1
1
V
UB7 = 3EI 2 · 47, 80 · 4, 5 · 23 · 4, 5 = 107,55
EI .
2
Ясно, что UBV8 = 0. Таким образом,
UBV =
7
X
UBjV =
j=1
1
(73, 71 + 169, 01 + 36, 84 + 40, 64+
EI
+ 297, 30 − 22, 44 + 107, 55 + 0) =
702, 61
м.
EI
5.4. Горизонтальное перемещение сечения B. После приложения в
сечении B единичной горизонтальной силы вычисляются опорные реакции. Это делается обычным образом, поэтому подробные выкладки
опускаются.
Итак,
P
MBпр = 0: R5 = 0;
= 0, 583;
P
P
ME = 0: R4 = −0, 583;
MAлев = 0: R1 = 0, 318;
P
пр
P
MK = 0: R2 =
MA = 0: R3 = −0, 682.
74
Статически определимые конструкции
H
Проверки X = 0 и Y = 0 выполняются. Эпюра "M B " строится по
правилам, знакомым по задаче 1.
H
V
На участках 1–4 эпюры "M B " и "M B " подобны. Коэффициент
подобия κ таков:
1, 75
= −0, 778.
κ=−
2, 25
Стало быть,
P
P
UBH = −0, 788
4
X
j=1
V
+
UBj
7
X
H
,
UBj
j=5
где (см. эпюру "M" на с. 70)
UBH5 = −
2
(2 · 54, 18 · 1, 75 + 2 · 57, 42 · 2, 39 + 54, 18 · 2, 39+
6EI
231, 36
.
+ 57, 42 · 1, 75) = −
EI
H
V
На следующем участке, т. e. на участке 6, фигуры "M B6 " и "M B6 "
подобны с коэффициентом κ = 2, 39/1, 43 = 1, 671, поэтому
37, 5
.
EI
= 0 и подвести черту под производимыми
V
H
= 1, 671 · (−22, 44) = −
= 1, 671 · UB6
UB6
H
Остается учесть, что UB7
вычислениями:
0, 788
(73, 71 + 169, 01 + 36, 84 + 40, 64)−
UBH = −
EI
517, 98
231, 36 37, 50
−
+0=−
м.
−
EI
EI
EI
Отрицательный знак говорит о том, что горизонтальное перемещение
сечения B противоположно направлению силы PBH = 1.
5.5. Угол поворота поперечного сечения C. К сечению C прикладывается единичный момент, после чего вычисляются опорные реакции рамы и строится эпюра изгибающих моментов M C , приведенная
в начале следующей страницы.
Далее с помощью эпюры "M " (см. с. 70) выполняются вычисления
V
по формуле (5.1). При этом учитывается подобие фигур "M C " и "M B "
на участках 1, 3, 4 и 6 с коэффициентами подобия:
κ1 = κ6 = −
0, 5
0, 318
= −0, 222; κ3 = κ4 =
= 0, 222.
1, 43
2, 25
75
Задача 5
Тогда
UC 2 =
UC 5 =
2
(2 · 47, 43 · 0, 5 + 2 · 44, 18 · 0, 682 + 47, 43 · 0, 682+
6EI
54, 04
+ 44, 18 · 0, 5) =
;
EI
2
(2 · 54, 18 · 0, 5 + 2 · 57, 42 · 0, 318 + 54, 18 · 0, 318+
6EI
45, 55
,
+ 57, 42 · 0, 5) =
EI
UC = 0, 222(−UBV1 + UBV3 + UBV4 − UBV6 ) + UCV2 + UCV5 =
=
Задача решена.
0, 222
· (−73, 71 + 36, 84 + 40, 64 + 22, 44)+
EI
105, 41
54, 04 45, 55
+
=
рад.
+
EI
EI
EI
76
Статически определимые конструкции
Задача 6. Определение перемещений в трехшарнирной арке
Условие задачи приводится на с. 15.
6.1. Предварительные замечания. Перемещение UC поперечного сечения C стержня с криволинейной осью находят по формуле
UC =
Zl 0
MC M
N N
Q Q dx
+ C +µ C
.
EI
EF
GF cos ϕ
(6.1)
В этом выражении MC , NC , QC – усилия от единичного воздействия,
приложенного по направлению искомого перемещения; M , N , Q – усилия от заданной нагрузки (см. задачу 2, с. 40–46), µ – коэффициент
формы поперечного сечения. Модуль сдвига G связан с модулем упругости E равенством
E
,
G=
2(1+ν)
где ν – коэффициент Пуассона. Так как (см. текст задания на с. 15)
b = ρh, h = 0, 02l, то
I=
bh3
ρh4
ρl4
=
=
· 10−6 ,
12
12
75
F = bh = ρh2 =
ρl2
· 10−2 .
25
Остается учесть, что E = 108 кН/м2 , µ = 1, 2 (известная величина для
прямоугольного сечения) и придать формуле (6.1) следующий вид:
10−4
UC =
4ρl2
Zl h
0
i dx
3 · 104
M
M
+
N
N
+
3Q
Q
.
C
C
C
l2
cos ϕ
(6.2)
В круглые скобки заключены слагаемые, определяющие вклад в искомое перемещение продольных и поперечных сил.
Взять интеграл (6.2) в замкнутом виде удается лишь в редких случаях. Для численного интегрирования здесь используется способ трапеций при разбиении интервала [0, l] на 16 равных участков. Расчетная
формула этого способа имеет вид:
15
MCi Mi
1 h
10−4 n 3 · 104 X
N N + NC,16 N16 +
+
UC ≈
64ρl
l2 i=1 cos ϕi
2 cos ϕi C0 0
77
Задача 6
+3 QC0 Q0 + QC,16 Q16
i
+
15
X
NCi Ni +3QCi Qi o
i=1
cos ϕi
.
(6.2a)
При записи формулы (6.2a) учитывалось, что в сечениях 0 и 16, т. е.
в шарнирах, изгибающие моменты отсутствуют и cos ϕ16 = cos ϕ0 . Далее в формуле (6.2a) вместо значка приближенного равенства будет
использоваться значок "=".
Соотношение (6.2a) позволяет найти любое перемещение в арке постоянного прямоугольного сечения в том случае, когда E = 108 кН/м2 ,
ν = 0, 25 и h = 0, 02l. Данное соотношение можно еще более конкретизировать, как только речь пойдет о вычислениях конкретного перемещения в конкретном поперечном сечении. Так, при вычислении
взаимного угла поворота сечений, примыкающих к замковому шарниру C, нужно к этим сечениям приложить единичные моменты PC ,
которые осуществляют вращение в разные стороны (см. рисунок, помещенный выше), найти опорные реакции от такого воздействия, а
затем по формулам (2.1), приведенным на с. 38, вычислить усилия
MC , NC , QC .
P
P
Условия равновесия
MA = 0 и MB = 0 дают VA = VB = 0. Это и
понятно: направленные навстречу друг другу единичные моменты PC
P
P пр
самоуравновешены. Тогда из уравнения
MCлев = 0 (или
MC = 0)
вытекает, что H = 1/f . Таким образом, вертикальные силы отсутству0
0
ют, а потому не будет и балочных усилий M , Q . В этом случае из
упомянутых выше формул (2.1) следует, что
y
MC = − ,
f
QC = −
sin ϕ
,
f
NC = −
cos ϕ
.
f
(6.3)
78
Статически определимые конструкции
С помощью этих формул зависимости (6.2a) придается окончательный
вид (учитывается, что sin ϕ16 = − sin ϕ0 ):
UC = −
15
10−4 n 3 · 104 X
yi Mi h 1 +
N
+
N
16 +
64ρf l
l2 i=1 cos ϕi
2 0
15 io
X
3
.
Ni + 3Qi tgϕi
+ Q0 − Q16 tg ϕ0 +
2
i=1
(6.4)
6.2. Вычисления. Ведутся в среде Excel с использованием данных,
полученных при решении задачи 2. Речь идет о величинах Mi , Qi , Ni ,
yi , cos ϕi и tg ϕi , а также о параметрах l = 26 м, f = 8 м, ρ = 1/3,
характеризующих геометрию конструкции. Тогда
n
UC = −2, 253606 · 10−8 44, 37867
15
X
+N16 +
i=1
i=1
i h3
Ni +
2
15
X
yi Mi
cos ϕi
Q0 −Q16 +3
15
X
+
h1
2
Qi tg ϕi
i=1
N0+
(6.4a)
io
.
Эта формула состоит из трех частей, отражающих вклад в искомое
перемещение изгибающих моментов, продольных сил и поперечных
сил соответственно.
Так как определяется угол поворота, то искомый результат измеряется в радианах. Табличная форма программы Excel приводится
на следующей странице (табл. 6.1). В столбце A этой таблицы указаны номера расчетных сечений арки. В столбцах B–D приведены
геометрические характеристики арки, позаимствованные из табл. 2.2,
помещенной на с. 48. Последняя является следствием силового расчета
рассматриваемой конструкции в среде Excel. В столбцах I–K табл. 2.2
даны значения всех трех усилий в расчетных сечениях арки. Эти усилия, необходимые при вычислениях по формуле (6.4a), переносятся в
столбцы E–G табл. 6.1. В клетки H5 и I5 вводятся формулы
= B5 ∗ E5/C5,
= F 5 ∗ D5/C5,
при помощи которых находят суммы, входящие в соотношение (6.4a).
Необходимые для вычислений выражения (видны по формуле (6.4a))
Задача 6
79
вводятся в ячейки K11, K12 и K13. Наконец, в поле K14 приводится суммарный результат. Отрицательный знак свидетельствует о том,
что сечения, расположенные по обе стороны от ключевого шарнира,
повернулись друг относительно друга в направлениях, противополож-
80
Статически определимые конструкции
ных направлениям сосредоточенных моментов, изображенных на рисунке, который помещен на с. 77.
Если находить перемещение в арке, учитывая влияние на него только деформации изгиба (что обычно и делается для конструкций, состоящих из призматических стержней), то результат был бы таким:
UC (M ) = −3, 4906 · 10−5 рад.
Добавление же сюда доли
UC (N ) = 1, 3412 · 10−5 рад,
обусловленной осевой деформацией арки, изменит величину искомого
перемещения UC на 38,4 %:
UC (M, N ) = −2, 1494 · 10−5 рад.
Если же учесть и слагаемое
UC (Q) = −9, 0330 · 10−8 рад,
порожденное только деформацией сдвига, то будет получен результат,
почти не отличающийся от предыдущего:
UC = −2, 15844 · 10−5 рад.
Различие в 0,4 % можно в расчет не принимать. Однако вовсе не всегда
влияние силы N на окончательный результат столь велико, а силы Q –
столь незначительно, как это получилось в рассмотренном примере, и
так как о таком влиянии заранее ничего сказать нельзя, то лучше всего
при расчете арок находить перемещения с учетом всех трех слагаемых
в формуле Мора.
81
Задача 7
Задача 7. Определение перемещений в плоской ферме
Условие задачи приводится на с. 15.
7.1. Предварительные замечания. Формула Мора, определяющая
узловые перемещения ферм, такова:
Uk =
C
X
Ni N ki
i=1
EFi
Li .
(7.1)
Здесь k – номер узла фермы, перемещение которого вычисляется, i
– номер стержня конструкции, Ni и N ki – усилия в i-ом стержне от
заданной нагрузки и от воздействия Pk = 1, приложенного в узле k
по направлению искомого перемещения, EFi и Li – осевая жесткость
и длина стержня с номером i. Предполагается, что опорные стержни
являются абсолютно жесткими, а потому C – это число только неопорных стержней. Если к тому же EFi = const, т. е. все стержни имеют
одинаковые осевые жесткие, то формула (7.1) примет вид:
Uk =
C
1 X
Ni N ki Li .
EF i=1
(7.2)
7.2. Вычисления. Подробного рассказа об использовании электронных таблиц при расчете арки достаточно, чтобы теперь и прогиб в
середине пролета фермы находить в среде Excel. Так и следует поступать, но предварительно полезно познакомиться с рациональной
организацией вычислений на примере, исполненном вручную.
Итак, требуется найти прогиб центрального узла нижнего пояса
фермы, которая рассматривалась при решении задачи 4. Речь идет
82
Статически определимые конструкции
об узле D изображенной выше конструкции. Дело сводится к последовательному заполнению полей табл. 7.1, макет которой диктуется
формулой (7.2) и которая приведена ниже. Первый столбец таблицы
содержит номера стержней. Конструкция и постоянное воздействие на
нее симметричны, поэтому в сумме (7.2) можно учесть только стержни левой половины фермы, а затем удвоить результат. Однако стойка 10 симметричного себе стержня не имеет. Чтобы обратить внимание
на это обстоятельство, номер 10 указанной стойки помечен в таблице
штрихом. Тем не менее ради однотипности вычислительных операций
прогиб в середине пролета фермы находят по формуле
UD =
13
2 X
Ni N Di Li ,
EF i=1
(7.3)
но длину стержня 10′ берут вдвое короче: L′10 = 8, 5/2 = 4, 25 м. Это
значение и помещается в соответствующее поле таблицы. Длины наклонных стержней находят по теореме Пифагора. Например,
L6 =
q
2, 52 + 3, 52 = 4, 301 м.
Таблица 7.1
Номера
стержней
2
3
4
5
6
7
8
9
10′
11
12
13
P
Li
м
Ni
кН
N Di
Ni NDi Li
3,5
3,5
3,5
3,5
4,301
6
6
6
4,25
6,946
6,946
9,192
28,07
35,66
-28,07
-44,91
-55,22
-48,12
-28,88
-32,09
19,25
55,72
33,44
24,29
0,2942
0,6175
-0,2942
-0,5835
-0,7170
-0,5
-0,5
-0,4167
1
0,5790
0,5790
-0,0901
28,90
77,07
28,90
91,72
170,29
144,36
86,64
80,23
81,81
224,09
134,49
-20,12
1128,38
Третий столбец таблицы содержит усилия в конструкции от постоянного воздействия. Так как N1 ≡ 0, информация о стержне 1 в таблице
83
Задача 7
отсутствует. Усилия в остальных стержнях были найдены при решении задачи 4 (см. столбец 4 табл. 4.1 на с. 67) и их значения теперь
напрямую переносятся в третий столбец табл. 7.1.
В четвертом столбце таблицы 7.1 проставляются значения усилий в
стержнях левой половины фермы от воздействия PD = 1, показанного
на расчетной схеме конструкции (см. с. 81). Эти усилия были найдены
при решении задачи 4. Их значения – суть центральные ординаты
изображенных на с. 65–66 линий влияния.
Наконец, в последнем столбце таблицы приводятся результаты перемножения чисел, находящихся в трех предыдущих столбцах. Сумма
этих произведений, равная 1128,38 единицам, записана в конце столбца 5. Согласно формуле (7.3),
UD =
2256, 76
2
· 1128, 38 =
м.
EF
EF
Представляет интерес численная оценка перемещения UD . Пусть
ферма выполнена из мягкой стали, прочность которой лимитируется
допускаемым напряжением [σ] = 16 · 104 кН/м2 , а жесткость – модулем
упругости E = 2 · 108 кН/м2 . Наиболее напряжен стержень с номером 11, воспринимающий продольную силу в 55,72 кН. Его прочность
будет обеспечена при
F =
N11
55, 72
=
≈ 3, 5 · 10−4 м2 .
[σ]
16 · 104
Тогда EF = 2 · 108 · 3, 5 · 10−4 = 7 · 104 и
UD =
2256, 76
2256, 76
=
= 0, 0322 м.
EF
7 · 104
Этот прогиб центрального узла, равный 3,22 см, чуть меньше одной
шестисотой пролета фермы:
l/600 = 21/600 = 0, 035 > 0, 0322.
Реализация таблицы 7.1 в программе Excel затруднений вызвать
не может, так что рассказ об этой процедуре опускается.
ЧАСТЬ III. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
КОНСТРУКЦИЙ
Задача 8. Расчет плоской рамы методом сил
Текст задания приведен на с. 16–17. Схема конструкции дана на
рис. 11. Перед выполнением работы следует по любому из литературных источников (учебнику, учебному пособию), ознакомиться с основами расчета статически неопределимых конструкций методом сил. В
пособии [1] необходимый материал содержится на с. 442–457.
8.1. Расчетная схема. Изображается при помощи рис. 11 (см. с. 27)
и табл. 5. Параметры конструкции и нагрузки на нее определяет шифр
843. Так как ρ = EIс /EIр = 1/4, то принимается EIс = EI, EIр =
4EI. Заданные нагрузки размещены на конструкции в соответствии
с указанием, имеющимся в тексте задания. Стержень с бесконечной
осевой жесткостью (распорка) воспринимает лишь продольную силу.
8.2. Основная система и усилия в ней. Число лишних связей, т. е.
степень статической неопределимости рассчитываемой конструкции,
может быть установлено по формуле
n = 3K − H,
в которой K – число замкнутых контуров рамы, H – количество шарниров. Подвижная опора при подсчете числа H рассматривается как
два шарнира. Поскольку данная рама имеет четыре замкнутых контура (K = 4) и в ней расположены два обычных шарнира и три опорных
стержня, т. е. H = 2 + 3 · 2 = 10, то n = 3 · 4−10 = 2.
85
Задача 8
Правильность подсчета числа n подтверждает представленная на рисунке основная
система: она неизменяема и получается из
заданной конструкции при устранении в таковой именно двух связей.
Далее в основной системе строятся единичные ("M 1 " и "M 2 ") и грузовая ("M0 ")
эпюры.
Э п ю р а "M 1 " порождается силой X1 = 1, приложенной по направлению первой устраненной связи. Построение этой единичной эпюры
начинается с определения опорных реакций основной системы, т. е. со
следующих вычислений:
ΣX = 0 → R2 = 0; ΣMCпр = 0: R1 ·2, 5−1· 4, 5 = 0 → R1 = 1, 8;
ΣMA = 0: R3 · 5, 5 − R1 · 5 = 0 → R3 = 1, 636;
P
Y = 0: R4 + R1 + R3 = 0 → R4 = −3, 436.
Затем при помощи метода сечений находят ординаты эпюры "M 1 "
и откладывают их на осевом контуре рамы со стороны растянутых
волокон (см. задачу 1)
Э п ю р а "M 2 " строится от воздействия X2 = 1. Опорные реакции
находят в той же последовательности, что и при построении эпюры
"M 1 ". Результаты получаются следующими:
R2 = 0, R1 = −3, 2, R3 = −1, R4 = 3, 2.
Затем вычисляются значения изгибающих моментов в характерных
сечениях рамы и вычерчивается график, отображающий полученные
результаты. Он приведен в начале следующей страницы.
86
Статически неопределимые конструкции
Э п ю р а "M0 " строится в основной системе только от заданного
силового воздействия. И здесь построение начинается с вычисления
опорных реакций в той же самой последовательности, которая была
принята при нагрузке X1 = 1. Результаты вычислений таковы:
R2 = −6 кН, R1 = 20, 79 кН, R3 = 2, 22 кН, R4 = −33, 11 кН.
8.3. Коэффициенты канонических уравнений. Система канонических уравнений метода сил при n = 2 имеет вид:

u11 X1 + u12 X2 + U10 = 0, 
(8.1)
u21 X1 + u22 X2 + U20 = 0. 
Единичные коэффициенты uik и свободные члены Ui0 канонических
уравнений определяются формулами Мора:
uik = (M i , M k ),
Ui0 = (M i , M 0 ).
(8.2)
Данные перемещения вычисляются по формуле (5.1) «перемножения»
эпюр, приведенной на с. 68:
uik =
C
X
ω ij mij
j=1
EIj
,
Ui0 =
C
X
Ω0j mij
j=1
EIj
.
(8.2a)
87
Задача 8
Имеет смысл предварительно преобразовать зависимости (8.2a), умножая каждую из них на некоторую жесткость EI0 , называемую далее
условной изгибной жесткостью. Величина EI0 вводится под знак суммы и отношение EI0 /EIj обозначается через αj :
αj = EI0 /EIj .
В результате формулы (8.2a) приобретут более удобную для их использования форму:
uik =
C
X
j=1
αj ω ij mij ,
Ui0 =
C
X
αj Ω0j mij .
(8.3)
j=1
Числа αj называют коэффициентами податливости стержней конструкции. Величину EI0 подбирают с таким расчетом, чтобы коэффициенты αj имели порядок, близкий к единице. Последние для удобства
вычислений указывают на основной системе рядом с соответствующими стержнями. Получившееся изображение именуют схемой податливости конструкции. При EI0 = 4EI эта схема имеет вид, представленный на рис. a.
Порядок вычислений по формуле (8.3) таков:
1) ставится знак произведения перемножаемых эпюр (положительный, если обе эпюры отложены с одной стороны рассматриваемого
стержня);
2) со схемы податливости записывается число αj ;
3) вычисляется площадь одной из эпюр на данном участке;
4) записывается ордината второй из перемножаемых эпюр (обязательно прямолинейной), отвечающая положению центра тяжести первой эпюры.
Эти операции выполняются на каждом из C участков рамы и полученные результаты складываются.
88
Статически неопределимые конструкции
Итак (см. рисунки на с. 85–86),
1
2
2
1
u11 = (M 1 , M 1 ) = 1· ·5, 5· 9 · · 9+2 · 1· ·2, 5· 4, 5 · · 4, 5 +
2
3
2
3
1
2
+2 · 4· ·4, 5· 4, 5 · · 4, 5 = 148, 5+33, 75+243 = 425, 25;
2
3
u12 = (M 1 , M 2 ) = −1 ·
2
1
· 5, 5 · 9 · · 5, 5−
2
3
1
2
−2 · 1· ·2, 5· 4, 5 · · 5, 5 = −90, 75−41, 25 = −132;
2
3
u22 = (M 2 , M 2 ) = 2 · 1 ·
+1 ·
2
1
· 2, 5 · 5, 5 · · 5, 5 = 110, 91 + 50, 42 = 161, 33;
2
3
U10 = (M 1 , M0 ) = 1·
−4·
2
1
· 5, 5 · 5, 5 · · 5, 5+
2
3
1
2
2
1
·5, 5· 9 · · 12, 22+2 · 1· ·2, 5· 4, 5 · · 27, 22 −
2
3
2
3
1
·4, 5·4, 5·15 = 201, 71+204, 19−607, 5 = −201, 6;
2
1
2
1
U20 = (M 2 , M0 ) = −1· ·5, 5·5, 5· ·12, 22−2 · 1· ·2, 5· 5, 5·
2
3
2
2
1
3
· · 27, 22 − 1 · ·5, 5· 27, 22 · · 5, 5 =
3
3
4
= −123, 27 − 249, 56 − 205, 19 = −578, 72.
Для проверки правильности вычислений образуют суммарную единичную эпюру
M S = M1 + M2,
показанную на с. 87 (рис. b), после чего эта эпюра умножается сама на
себя:
1
2
2 1
· 5, 5 · 3, 5 · · 3, 5+2 1 · · 2, 5 · 1 · · 1 +
2
3
2
3
1
1
2
2
+1 · · 5, 5 · 5, 5 · · 5, 5 + 2 4 · · 4, 5 · 4, 5 · · 4, 5 =
2
3
2
3
S
S
(M , M ) = 1 ·
= 22, 46 + 1, 66 + 55, 46 + 243 = 322, 58.
89
Задача 8
С другой стороны,
2
X
uik = u11 +u22 + 2u12 = 425, 25+161, 33−2 · 132 = 322, 58.
i,k=1
Поскольку
S
S
(M , M ) =
2
X
uik ,
i,k=1
единичные коэффициенты найдены правильно.
Далее делается проверка свободных членов канонических уравнений. Для этого вычисляется интеграл
1
2
2
1
S
(M , M0 ) = 1· ·5, 5·3, 5· ·12, 22−2 1· ·2, 5·1· ·27, 22 −
2
3
2
3
1
1
3
−1 · · 5, 5 · 27, 22 · · 5, 5−4 · · 4, 5 · 4, 5 · 15 =
3
4
2
= 78, 45 − 45, 38 − 205, 89 − 607, 5 = −780, 32
и сумма
2
X
Ui0 = U10 + U20 = −201, 6 − 578, 72 = −780, 32.
i=1
Результаты совпали, стало быть, свободные члены канонических уравнений найдены верно.
8.4. Решение системы канонических уравнений. После подстановки в систему (8.1) вычисленных единичных коэффициентов и свободных членов она примет следующий вид:

425, 25 X1 − 132, 00 X2 − 201, 60 = 0, 
− 132, 00 X1 + 161, 33 X2 − 578, 72 = 0. 
(81a)
Если первое из этих уравнений разделить на 425,25, второе – на 132,
а затем сложить результаты, то получится равенство
0, 9118 X2 − 4, 8583 = 0,
из которого сразу же следует, что X2 = 5, 3283. Тогда первое из уравнений (8.1a) дает X1 = 2, 1280.
90
Статически неопределимые конструкции
Проверка правильности полученного решения осуществляется следующим образом. Сначала образуют суммарное каноническое уравнение, складывая уравнения системы (8.1a):
293, 25 X1 + 29, 33 X2 − 780, 32 = 0,
в которое затем вводят найденные значения X1 и X2 основных неизвестных:
293, 25 · 2, 128 + 29, 33 · 5, 3283 − 780, 32 =
= 624, 04 + 156, 28 − 780, 32 = 780, 32 − 780, 32 ≡ 0.
Получившееся тождество говорит о том, что система (8.1a) решена
правильно. Таким образом,
X1 = 2, 1280,
X2 = 5, 3283.
8.5. Эпюра изгибающих моментов. Формула для усилия M следует
из принципа наложения: M = M0 + M 1 X1 + M 2 X2 . Построенная по
этой формуле эпюра подлежит двум проверкам.
Статическая проверка сводится к контролю за равновесием узлов.
Как видно из приводимого в начале следующей страницы рисунка, эта
проверка удовлетворяется.
91
Задача 8
Кинематическая проверка позволяет убедиться в отсутствии у заданной конструкции перемещений по направлениям сил X1 и X2 , т. е.
по направлениям реально существующих связей. Она сводится к проS
верке выполнения равенства (M, M ) = 0. Необходимые для вычислений рисунки помещены на с. 87 и 90.
1
1
2
2
· 5, 5 · 3, 5 · · 2, 07−2 1 · · 2, 5 ·1· · 7, 49 +
2
3
2
3
1
2
2
1, 8 · 5, 52 1
· 5, 5 · 2, 09 · · 5, 5+ · 5, 5 ·
· · 5, 5 −
+1·
2
3
3
8
2
2
1
1
1
2
− 4 · · 4, 5 · 4, 5 · 5, 42+ · 15 +4 · · 4, 5 · 4, 5 · · 9, 58 =
2
3
3
2
3
S
(M, M ) = 1·
= 13, 28−12, 48+ 89, 74−348, 84+258, 66 = 361, 68−361, 32 ≈ 0.
И в самом деле, разность между числами 361,68 и 361,32, равная
0,34, составляет менее 0,1% от меньшего из них, что вполне можно
считать нулевой погрешностью. Эпюра "M " построена правильно.
8.6. Поперечные и продольные силы. Эпюра "Q" строится по эпюре "M ". Для этого рама разбивается на участки так, как это показано на рисунке, приведенном по завершению настоящего абзаца, а
затем рассматривается равновесие каждого участка, отделенного от
конструкции двумя разрезами. В каждом разрезе прикладываются
усилия M , Q и N , причем величина M известна. Останется лишь составить условия равновесия так, чтобы в каждое из них входила только одна неизвестная величина – поперечная сила. Поперечные силы
изображаются на выделенном элементе положительными, т. е. вращающими его по ходу часовой стрелки. Значения изгибающих моментов
берутся с эпюры "M ", позволяющей установить также (по растяну-
92
Статически неопределимые конструкции
тым волокнам) их направления. Все остальное ясно из вычислений,
которые приведены ниже. Ясно также и то, что на рисунках не было
необходимости изображать усилия N , ибо в составляемые уравнения
равновесия продольные силы не входят.
Задача 8
93
Равновесие участка № 7 даже не рассматривалось. Дело в том, что
активная нагрузка к правой нижней стойке рамы не прикладывалась,
а реакция подвижной опоры направлена по оси обсуждаемого стержня, стало быть, Q13 = Q14 ≡ 0.
По полученным данным и построена эпюра "Q", изображенная на
следующей странице рядом с эпюрой продольных сил.
При вычислении продольных сил учитывается, что на участках 1
и 3 они равны нулю: ведь по концам названных участков установлены
подвижные опоры. Итак, N1 = N2 = N5 = N6 = 0. Далее рассматривается равновесие отделенных от рамы узлов 1 и 2. В местах разрезов
прикладываются только что найденные усилия Q (положительные поперечные силы направлены так, чтобы они вращали рассматриваемый
узел по часовой стрелке), а также искомые продольные силы. Последние изображаются положительными, т. е. растягивающими стержень.
Изгибающие моменты в составляемые условия равновесия узлов не
входят, а потому на рисунке их не указывают.
94
Статически неопределимые конструкции
Ясно, что N8 = N11 = N12 = N7 , N10 = N13 = N14 = N9 , а усилие в
распорке равно силе X1 : Nрас = X1 = 2, 13 кН. Эпюра "N " показана
рядом с эпюрой поперечных сил.
По эпюрам "Q" и "N " устанавливают опорные реакции в раме и
выполняют окончательную статическую проверку:
P
P
X = 0 : 6 − 6 = 0;
Y = 0 : 9, 9 − 0, 38 − 5, 33 +
+ 3, 88 − 7, 57 =
= 13, 28 − 13, 28 ≡ 0.
На этом вычисления заканчиваются. Задача решена.
Задача 9
95
Задача 9. Расчет плоской рамы методом перемещений
Текст задания приведен на с. 17–19. Схема конструкции дана на
рис. 11. Перед выполнением работы следует по любому из литературных источников (учебнику, учебному пособию) ознакомиться с основами расчета статически неопределимых конструкций методом перемещений. В пособии [1] необходимый материал содержится на с. 486–502.
Единичные и грузовые состояния метода перемещений получают при
помощи данных, содержащихся в табл. 9.1, расположенной на следующей странице.
9.1. Расчетная схема. Изображается при помощи рис. 11 и табл. 6.
Параметры конструкции определяет шифр 843. Так как ρ = EIс /EIр =
= 0, 4, то принимается EIс = EI, EIр = 2, 5EI. Заданные нагрузки
размещены на конструкции в соответствии с указанием, имеющимся в
тексте задания.
9.2. Основная система. Степень кинематической неопределимости
рамы равна трем: возможны независимые повороты двух жестких узлов конструкции и их совместное перемещение по горизонтали. К основной системе приходят, накладывая две поворотные и одну линейную связи так, как это показано на рисунке.
96
Статически неопределимые конструкции
На основной системе указываются положительные направления углов поворота Z1 , Z2 и линейного перемещения Z3 жестких узлов рамы, а также условные погонные жесткости Jk стержней. Если принять
EIс /lс = EI/6, 5 = 1 (т. е. положить EI = 6, 5), то погонные жесткости
левого, среднего и правого горизонтальных стержней будут такими:
Таблица 9.1. Изгибающие моменты и опорные реакции
для призматических стержней
97
Задача 9
2, 5EI 2, 5 · 6, 5
2, 5EI 2, 5 · 6, 5
=
= 2, 708,
=
= 3, 25,
6
6
5
5
2, 5EI 2, 5 · 6, 5
=
= 2, 5.
6, 5
6, 5
9.3. Единичные и грузовые эпюры. Строятся в основной системе
при помощи табл. 9.1 только на тех стержнях, которые деформируются при рассматриваемом воздействии. При единичных перемещениях
наложенных связей изгибаются лишь те стержни, которые опираются
на смещаемую связь, а при заданном силовом воздействии – исключительно те стержни, к которым непосредственно это воздействие прикладывается. Сказанное иллюстрирует приводимый ниже рисунок.
98
Статически неопределимые конструкции
Ординаты эпюр откладываются со стороны растянутых волокон
элементов рамы, при их вычислении учитываются приведенные погонные жесткости стержней, указанные на основной системе. Например,
ордината эпюры "M1" на левом ригеле рамы вычисляется следующим
образом (см. табл. 9.1):
m1 = 3J = 3 · 2, 708 = 8, 124,
а ординату эпюры "M 3 " на правой стойке конструкции находят так:
m3 = 6J/l = (6 · 1)/6, 5 = 0, 9231.
Характерные ординаты эпюры "M0 " на ригеле и стойке таковы:
mр =
P l 7 · 6, 5
ql2 2, 6 · 62
=
= 11, 7, mс =
=
= 5, 688.
8
8
8
8
9.4. Коэффициенты и свободные члены системы канонических
уравнений. Названная система при n = 3 имеет следующий вид:

r11 Z1 + r12 Z2 + r13 Z3 + R10 = 0, 


r21 Z1 + r22 Z2 + r23 Z3 + R20 = 0,
r31 Z1 + r32 Z2 + r33 Z3 + R30

(9.1)



= 0. 
Реакции rik и Ri0 удобно найти статическим способом, прямо опираясь
на физический смысл этих величин.
Реакция поворотной связи представляет собой реактивный момент.
По эпюре "M 1 " видно, что реактивный момент r11 , который возникает в первой наложенной связи от ее же смещения на единицу, складывается из реактивных моментов трех примыкающих к этой связи
стержней:
r11 = 8, 124 + 13 + 3 = 24, 124.
Важно подчеркнуть, что так называемые собственные реакции, т. е.
реакции с двумя одинаковыми индексами, всегда положительны. Реакции r12 и r13 устанавливают соответственно по эпюрам "M 2 " и "M 3 ":
r12 = 6, 5,
r13 = −0, 4615.
Реакция r12 взята со знаком "+" потому, что ордината 6,5 эпюры
"M 2 "отложена от оси среднего ригеля рамы в ту же сторону, что и
99
Задача 9
положительная ордината 13 на эпюре "M 1 ". Ординаты 0,4615 и 3 на
эпюрах "M 3 " и "M 1 " находятся по разные стороны от оси левой стойки, поэтому реакция r13 отрицательна. По эпюре "M0 " видно, что
R10 = 11, 7.
Аналогично по эпюрам усилий M 2 , M 3 и M0 находят реакции второй наложенной связи:
r22 = 13+7, 5+ = 24, 5, r23 = −0, 9231, R20 = −5, 688.
Реакция r33 представляет собой реакцию линейной связи. Эта реакция численно равна сумме поперечных сил, возникающих в стойках
основной системы при смещении третьей наложенной связи на единицу. Поперечную силу при линейной эпюре изгибающих моментов можно найти как тангенс угла наклона
фигуры "M ". Вычисления ведутся
с помощью эпюры "M 3 " и приводимого рядом рисунка:
пр
r33 = Qлев
ст +Qст =
0, 4615 0, 9231+0, 9231
+
= 0, 3550.
6, 5
6, 5
Реакция r33 положительна. Она направлена в ту же сторону, что и
перемещение Z3 = 1.
Реакция R30 возникает от воздействия P = 7 кН. Из таблицы 9.1
видно, что
R30 = P/2 = 3, 5
и что направлена она так же, как и реакция r33 , а потому и взята с
положительным знаком.
9.5. Решение системы канонических уравнений. В систему (9.1)
подставляются вычисленные выше коэффициенты rik = rki и свободные члены Ri0 :
24, 124 Z1 +
6, 5 Z1 +

6, 5 Z2 − 0, 4615 Z3 + 11, 700 = 0, 


24, 5 Z2 − 0, 9231 Z3 − 5, 688 = 0,




− 0, 4615 Z1 − 0, 9231 Z2 + 0, 3550 Z3 + 3, 500 = 0, 
(9.1a)
100
Статически неопределимые конструкции
после чего она решается методом Гаусса. Так как величины rik и Ri0
не слишком отличаются по своему порядку, можно применить тот вариант схемы Гаусса, который используется ниже.
Сначала делением уравнений системы (9.1a) соответственно на числа 24,124, 6,5 и 0,4615 таковая приводится к виду:
Z1 + 0, 2694 Z2 − 0, 01913 Z3 + 0, 4850 = 0,
Z1 + 3, 7692 Z2 − 0, 14202 Z3 − 0, 8751 = 0,
2 Z2 + 0, 76923 Z3 + 7, 5840 = 0.
−Z1 −
Затем исключается первое основное неизвестное:

(a) 



(b)



(c) 

(a)+(c) : −1, 7306 Z2 + 0, 7501 Z3 + 8, 0690 = 0, 
(b)+(c) :
1, 7692 Z2 + 0, 6272 Z3 + 6, 7089 = 0. 
Дальнейшие действия в комментариях не нуждаются.
−Z2 + 0, 4334 Z3 + 4, 6625 = 0,
Z2 + 0, 3545 Z3 + 3, 7921 = 0;

(a′ ) 
(b′ ) 
(a′ )+(b′ ) : 0, 7879 Z3 +8, 4546 = 0 → Z3 = −10, 73.
Из (a′ ) : Z2 = −0, 4334 · 10, 73 + 4, 6625 = 0, 0119.
Из (c) : Z1 = −2 · 0, 0119−0, 76923 · 10, 73+7, 584 = −0, 6937.
Для проверки правильности вычислений образуют суммарное каноническое уравнение, складывая все три уравнения системы (9.1a):
30, 1625 Z1 + 30, 0769 Z2 − 1, 0296 Z3 + 9, 512 = 0.
Подстановка сюда значений
Z1 = −0, 6937,
Z2 = 0, 0119,
Z3 = −10, 73
основных неизвестных дает:
−20, 9258 + 0, 3579 + 11, 0476 + 9, 5120 = −20, 9258 + 20, 9175.
Разность между этими числами равна 0,0083, что составляет менее
0,4 % от слагаемого 20,9175. Это говорит о высокой точности проделанных вычислений.
Задача 9
101
9.6. Изгибающие моменты. Изгибающие моменты находят по формуле
M = M0 + M 1 Z1 + M 2 Z2 + M 3 Z3 .
Каждая из четырех складываемых эпюр (см. нижеследующий рисунок) условиям равновесия узлов не удовлетворяет, тогда как их сумма
приводит к уравновешенной эпюре. Значит, искомая эпюра "M " верна.
9.7. Поперечные и продольные силы. Эпюру "Q" получают по эпюре "M " так, как об этом говорилось при решении задачи 8. Затем от
эпюры "Q" способом, также описанным при решении задачи 8, переходят к эпюре продольных сил. Наконец, раму изображают вместе
со всеми приложенными к ней нагрузками, включающими в себя и
опорные реакции, которые устанавливают по эпюрам "M ", "Q", "N ",
и делают окончательную статическую проверку. Надо убедиться, что
тождественно удовлетворяются любые три независимые условия равP
P
P
Y =0 и
MA = 0, где A –
новесия, например условия
X = 0,
любая характерная точка на расчетной схеме конструкции.
102
Статически неопределимые конструкции
На представленных ниже рисунках изображены как эпюры поперечных и продольных сил, так и схема загружения рамы, используемая для выполнения окончательной статической проверки.
103
Задача 10
Задача 10. Расчет неразрезной балки
Текст задания приведен на с. 19–20. Схема конструкции дана на
рис. 11. Перед выполнением работы следует по любому из литературных источников (учебнику, учебному пособию) ознакомиться с основами расчета неразрезных балок на постоянную нагрузку и построением
в них огибающих эпюр усилий. В пособии [1] необходимый материал
содержится на с. 468–470 и 481–484. В ходе расчета балки методом
сил сначала строятся эпюра "M C " от постоянной нагрузки и эпюры
"M (j) " от поочередного загружения всех пролетов балки временной
нагрузкой, а затем на их основе получают искомую огибающую эпюру
изгибающих моментов "M ог ".
10.1. Расчетная схема. Изображается при помощи рис. 11 и табл. 7.
Параметры конструкции и нагрузки на нее определяет шифр 843. При
назначении длины консоли (ее номер на рис. 11 отмечен штрихом) табличный размер был уменьшен в 5 раз. Временная равномерно распределенная нагрузка интенсивности p = 2, 2 кН/м может занимать любой
пролет (пролеты) балки, а также консольный участок. Поэтому балку
приходится рассчитывать четыре раза: на постоянное воздействие и
временную нагрузку в трех ее положениях.
10.2. Основная система и ее состояния. Балка имеет 2 лишние связи. Основная система, приводящая к локальным единичным и грузовым состояниям, получится, если ввести в защемленную опору шарнир
и еще одним шарниром разрезать балку над промежуточной опорой.
Единичные эпюры "M 1 " и "M 2 " строятся от моментных воздействий X1 = 1 и X2 = 1 соответственно. Кроме того, строятся четыре грузовых эпюры: "M0C " от постоянной нагрузки и "M0(1) ", "M0(2) "
и "M0(3) " от поочередного загружения двух пролетов и консольного
участка временной нагрузкой. Для удобства вычислений эпюра "M0C "
104
Статически неопределимые конструкции
на втором участке от силы P и равномерно
распределенной нагрузки интенсивности q2
разбита на две части.
10.3. Коэффициенты и свободные члены
канонических уравнений. Система канонических уравнений при n = 2 имеет вид:

u11 X1 + u12 X2 + U10 = 0, 
(10.1)
u21 X1 + u22 X2 + U20 = 0. 
В качестве свободных членов U10 и U20 здесь
каждый раз берутся перемещения, соответствующие тому из четырех воздействий, на
которое ведется данный расчет. Коэффициенты системы (10.1) от нагрузки на конструкцию не зависят. Их (как и свободные члены) можно находить в предположении, что
EI = 1. И в самом деле, поскольку правые
части уравнений (10.1) равны нулю, а изгибные жесткости всех участков балки одинаковы, данное допущение не скажется на значениях основных неизвестных. Порядок вычислительных операций рассматривался при решении задачи 8.
u11 = (M 1 , M 1 ) =
1
1
2
4
1
2
· 1 · 4 · · 1 = , u12 = (M 1 , M 2 ) = · 1 · 4 · · 1 = ,
2
3
3
2
3
3
u22 = (M 2 , M 2 ) =
1
2
1
2
6, 5
· 1 · 4 · · 1 + · 1 · 2, 5 · · 1 =
.
2
3
2
3
3
Далее вычисляются свободные члены канонических уравнений:
а. П о с т о я н н а я н а г р у з к а
C
= (M 1 , M0C ) =
U10
1
32
2
· 4 · 8 · · 1= ,
3
2
3
C
=
U20
1
2
1
1
1
17, 46
2
= (M 2 , M0C ) = ·4·8· ·1+ ·2, 734·2, 5· ·1− ·1·2, 5· ·17, 1 =
.
3
2
3
2
2
3
3
105
Задача 10
б. В р е м е н н а я н а г р у з к а н а п р о л е т е 1
1
17, 6
·1=
,
2
3
1
17, 6
·1=
.
2
3
2
· 4 · 4, 4 ·
3
2
= (M 2 , M0(1) ) = · 4 · 4, 4 ·
3
(1)
U10
= (M 1 , M0(1) ) =
(1)
U20
в. В р е м е н н а я н а г р у з к а н а п р о л е т е 2
(2)
= (M 1 , M0(2) ) = 0,
U10
(2)
U20
= (M 2 , M0(2) ) =
2
1
4, 30
· 2, 5 · 1, 719 · · 1 =
.
3
2
3
г. В р е м е н н а я н а г р у з к а н а к о н с о л и
(3)
U10
= (M 1 , M0(3) ) = 0,
1
1, 11
1
(3)
U20
= (M 2 , M0(3) ) = − · 2, 5 · 0, 891 · · 1 = −
.
2
3
3
Целесообразно все полученные перемещения умножить на 3. Это
упростит арифметические операции и никак не скажется на значениях
основных неизвестных:
u11 = 4,
C
U10
= 32,
C
= 17, 46,
U20
u12 = u21 = 2,
(1)
U10 = 17, 6,
(1)
U20
= 17, 6,
u22 = 6, 5;
(2)
(3)
U10 = U10
= 0;
(2)
U20
= 4, 30,
(3)
U20
= −1, 11.
10.4. Решение системы канонических уравнений. Таковую придется решать четыре раза – по числу воздействий. Проще всего это сделать при помощи правила Крамера:
X1 = −
D1
,
D
X2 = −
D2
,
D
где D – определитель системы (10.1):
u
D = 11
u21
u12
u22
= u11 u22 − u212 = 4 · 6, 5 − 22 = 22,
(10.2)
106
Статически неопределимые конструкции
а D1 , D2 – определители, которые следуют из определителя D при замене соответственно 1-го и 2-го столбцов на столбец свободных членов,
а именно:
U
D1 = 10
U20
u
D2 = 11
u21
u12
u22
U10
U20
= U10 u22 − U20 u12 = 6, 5 · U10 − 2 · U20 ,
= u11 U20 − u21 U10 = 4 · U20 − 2 · U10 .
По этим формулам и находят значения основных неизвестных при всех
четырех способах загружения конструкции:
а. П о с т о я н н а я н а г р у з к а
C
C
− 2U20
= 6, 5 · 32 − 2 · 17, 46 = 173, 1;
D1C = 6, 5U10
C
C
D2C = 4U20
− 2U10
= 4 · 17, 46 − 2 · 32 = 5, 84;
X1C = −
D1C
DC
173, 1
5, 84
=−
= −7, 87; X2C = − 2 = −
= −0, 265.
D
22
D
22
б. В р е м е н н а я н а г р у з к а н а п р о л е т е 1
(1)
(1)
− 2U20
= 6, 5 · 17, 6 − 2 · 17, 6 = 79, 20;
D1(1) = 6, 5U10
(1)
(1)
D2(1) = 4U20
− 2U10
= 4 · 17, 6 − 2 · 17, 6 = 35, 2;
X1(1) = −
D1(1)
D (1)
79, 2
35, 2
=−
= −3, 60; X2(1) = − 2 = −
= −1, 60.
D
22
D
22
в. В р е м е н н а я н а г р у з к а н а п р о л е т е 2
(2)
(2)
− 2U20
= 6, 5 · 0 − 2 · 4, 30 = −8, 60;
D1(2) = 6, 5U10
(2)
(2)
− 2U10
= 4 · 4, 30 − 2 · 0 = 17, 20;
D2(2) = 4U20
X1(2) = −
D (2)
17, 2
D1(2) 8, 60
=
= 0, 391; X2(2) = − 2 = −
= −0, 782.
D
22
D
22
г. В р е м е н н а я
нагрузка на консоли
(3)
(3)
D1(3) = 6, 5U10
− 2U20
= 6, 5 · 0 + 2 · 1, 11 = 2, 22;
(3)
(3)
− 2U10
= −4 · 1, 11 − 2 · 0 = −4, 44;
D2(3) = 4U20
X1(3) = −
D1(3)
D (3) 4, 44
2, 22
=−
= −0, 101; X2(3) = − 2 =
= 0, 202.
D
22
D
22
107
Задача 10
10.5. Огибающая эпюра изгибающих моментов. Усилие M от каждого из четырех загружений вычисляется по формуле
M = M0 +M 1 X1 +M 2 X2 .
В качестве M0 , X1 и X2 каждый раз берутся те изгибающие моменты
и те значения основных неизвестных, которые отвечают рассматриваемой нагрузке. В неразрезной балке построение эпюр облегчается тем,
что основные неизвестные представляют собой опорные моменты. Поэтому можно в соответствующих местах графика отложить найденные
выше значения X1 и X2 (положительные ординаты откладываются
вниз от оси балки), соединить полученные точки прямыми линиями и
добавить усилия M0 . Построенные таким образом эпюры изгибающих
моментов от всех четырех воздействий приводятся ниже.
Например, ординаты эпюры "M C " в серединах 1-го и 2-го пролетов балки (см. на рисунке точки 2 и 4), построенной от постоянной
нагрузки, находят так:
X1C +X2C
=
2
−7, 87 − 0, 265
= 3, 93;
=8+8+
2
XC
C
+ 2 =
M4C = M04
2
17, 1 0, 265
= −5, 95.
−
= 2, 734 −
2
2
C
M2C = M02
+
Ординаты огибающей эпюры вычисляются в
сечениях 1–5. Это делается в табличной форме. Результаты в графе "max M " таблицы 10.1
получены путем сложения усилий M C с теми значениями изгибающих моментов M (1) ,
M (2) , M (3) , которые имеют знак "+", а в графе "min M " – при сложении значений M C с
отрицательными ординатами эпюр "M (i) ".
Таблица 10.1, в которой приводятся результаты проведенных вычислений, размещена на следующей странице.
108
Статически неопределимые конструкции
Таблица 10.1
Усилия
1
C
M
M (1)
M (2)
M (3)
max M
min M
-7,87
-3,60
0,39
-0,10
-7,48
-11,57
Номера расчетных сечений
2
3
4
3,93
1,80
-0,20
0,05
5,78
3,73
-0,26
-1,60
-0,78
0,20
-0,06
-2,64
-5,95
-0,80
1,33
-0,34
-4,62
-7,09
5
-17,10
0
0
-0,89
-17,10
-17,99
109
Задача 11
Задача 11. Расчет двухшарнирной арки
Текст задания приведен на с. 21. Схема конструкции представлена
на рис. 11. Перед выполнением работы следует по любому из литературных источников (учебнику, учебному пособию) ознакомиться с
основами расчета статически неопределимых арок на постоянную нагрузку. В пособии [1] необходимый материал содержится на с. 470–473.
11.1. Расчетная схема. Её основой является схема арки, предложенная для решения задачи 2 (см. с. 40), только теперь отсутствует замковый шарнир C. Такая арка имеет одну лишнюю связь, а потому
представляет собой статически неопределимую конструкцию, расчет
которой выполняется методом сил.
11.2. Основная система. Единичные и грузовые эпюры. В качестве
основной системы (показана на следующей странице) удобнее всего
выбрать трехшарнирную арку, т. е. ту конструкцию, которая рассматривалась при решении задач 2 и 6. В этом случае не придется строить
грузовые эпюры "M0 ", "Q0 " и "N0 ", ибо именно такие эпюры были
уже построены в статически определимой трехшарнирной арке (задача 2). Значения усилий M0 , Q0 и N0 в расчетных сечениях приведены
в трех последних столбцах табл. 2.1, приведенной на с. 44 (см. также
с. 45).
Были также получены и описаны при решении задачи 6 единичные
усилия M 1 , Q1 и N 1 . И в самом деле, ведь при отыскании взаимного
угла поворота сечений, примыкающих к замковому шарниру, определялись изгибающие моменты, продольные и поперечные силы, возникающие в трехшарнирной арке как раз при действии сосредоточенных
моментов MC = 1. Речь идет об усилиях, аналитические выражения
(6.3) для которых приведены на с. 77. Другое воздействие MC = 1,
рассмотренное при решении задачи 6, ничем не отличается от воздей-
110
Статически неопределимые конструкции
ствия X1 = 1, прикладываемого к основной системе в рассматриваемой
задаче, а потому формулы, взятые со с. 77, указаны и на приводимом
ниже рисунке, однако записаны они уже с учетом того, что f = 8 м.
11.3. Формирование канонического уравнения. При n = 1 вместо
системы будет одно единственное каноническое уравнение
u11 X1 + U10 = 0.
(11.1)
Его формирование сводится к вычислению перемещений u11 и U10 .
Первое из них есть не что иное, как обусловленный действием пар
X1 = 1 взаимный угол поворота торцов полуарок, расположенных в основной системе по разные стороны от центрального (замкового) шарнира. Перемещение U10 представляет собой тот же угол поворота, но
порожденный уже не единичными моментами, а заданным силовым
воздействием.
О том, как находят перемещения в арках, рассказывалось при обсуждении задачи 6. При тех параметрах конструкции, о которых говорилось на с. 77, расчетная формула для взаимного угла поворота
111
Задача 11
поперечных сечений, примыкающих к замковому шарниру, была сведена к виду (6.4). Эта формула приводится здесь повторно:
UC = −
15
h1
10−4 n 3 · 104 X
yi Mi
+
N
+
N
16 +
64ρf l
l2 i=1 cos ϕi
2 0
(11.2)
15 io
X
3
.
Ni + 3Qi tgϕi
+ Q0 − Q16 tg ϕ0 +
2
i=1
Из этого равенства немедленно следует выражение для перемещения
u11 , если положить (см. рис. на предыдущей странице)
Mi ≡ M 1i = −
yi
sin ϕi
cos ϕi
, Qi ≡ Q1i = −
, Ni ≡ N 1i = −
f
f
f
и учесть, что cos ϕ16 = cos ϕ0 , sin ϕ16 = − sin ϕ0 , ρ = 1/3:
u11 =
15
3 · 10−4 h 3 · 104 X
yi2
+ cos ϕ0 +
64f 2 l
l2 i=1 cos ϕi
+ 3 sin ϕ0 tg ϕ0 +
15 X
cos ϕi + 3 sin ϕi tgϕi
(11.2a)
i
.
i=1
Это перемещение находят при помощи программы Excel (см. табл. 11.1
на следующей странице). Результат при l = 26 м, f = 8 м таков:
u11 = 6, 90347 · 10−5 .
Что же касается перемещения U10 , то оно дается непосредственно формулой (11.2) и в расчетной работе 6 было уже вычислено (см. с. 80):
U10 = −2, 15844 · 10−5 .
Следовательно (см. равенство (11.1),
6, 90347 · 10−5 X1 − 2, 15844 · 10−5 = 0, → X1 = 0, 31266.
Таким образом, каноническое уравнение не только сформулировано,
но и решено.
11.4. Вычисление усилий. Производится в среде Excel по формулам:
M = M 1 X1 + M0 , Q = Q1 X1 + Q0 , N = N 1 X1 + N0 .
(11.3)
112
Статически неопределимые конструкции
Единичные эпюры M 1 , Q1 , N 1 изображены на c. 110, а грузовые эпюры
– на с. 45.
Результаты построений по формулам (11.3), т. е. итоговые эпюры
изгибающих моментов, продольных и поперечных сил, представлены
на размещенном на следующей странице рисунке.
Выделять отдельные столбцы в таблице Excel для записи единичных усилий нет необходимости, поскольку их аналитические выражения элементарны (см. формулы (6.3) на с. 77 и рисунок на с. 110) и
их целесообразнее непосредственно включить в формулы для подсчета искомых усилий (11.3) в двухшарнирной арке, записав таковые в
виде:
sin ϕ
cos ϕ
y
X1 +Q0 , N = −
X1 +N0
M = − X1 +M0 , Q = −
8
8
8
или (подставляется значение X1 = 0, 3127)
113
Задача 11
M = −0, 0391y + M0 , Q = −0, 0391 sin ϕ+ Q0 , N = −0, 0391 cos ϕ+ N0 .
Значения вычисленных по этим формулам усилий M , Q и N в
расчетных сечениях содержатcя в трех последних столбцах таблицы,
помещенной на следующей странице.
При сопоставлении усилий в трехшарнирной и двухшарнирной арках, т. е. эпюр, приведенных на этой странице и на с. 45, обнаруживается практически полная их идентичность. Совпадение состояний
заданной конструкции (в данном случае – двухшарнирной арки) и ее
основной системы (трехшарнирной арки), хотя не так уж и часто, но
встречается. Например, если U10 = 0, то каноническое уравнение (11.1)
дает X1 = 0. Но тогда, согласно формулам (11.3),
M = M0 ,
Q = Q0 ,
N = N0 ,
т. е. усилия в заданной статически неопределимой конструкции и ее основной системе одинаковы. Если же U10 6= 0, но перемещение U10 мало,
114
Статически неопределимые конструкции
то малым будет и значение основного неизвестного X1 . В результате
первые слагаемые в правых частях формул (11.3) окажутся намного
меньше вторых слагаемых, а потому усилия в исходной конструкции
115
Задача 11
и ее основной системе будут близки друг к другу:
M ≈ M0 ,
Q ≈ Q0 ,
N ≈ N0 .
Описанная выше ситуация как раз и реализовалась в рассматриваемом примере. Объясняется это тем, что нагрузка прикладывается
только к одной половине арки, а потому усилие M0 , вклад которого
в перемещение U10 самый существенный, получилось близким к обратно симметричному: на левой половине арки изображенная на с. 45
эпюра "M0 " положительна, на правой – отрицательна, причем площади положительной и отрицательной частей эпюры примерно равны.
Единичная эпюра изгибающих моментов (см. с. 110) симметрична и
всюду имеет отрицательный знак. Вот почему интеграл Мора от произведения усилий M0 и M 1 оказался весьма малым и столь же малым получилось перемещение U10 . В результате основное неизвестное
X1 , равное значению 0, 3127ql2 изгибающего момента в замковом сечении двухшарнирной арки, вышло практически на два порядка меньше
наибольшего значения изгибающего момента в конструкции, равного
(примерно) величине 70ql2 .
116
Статически неопределимые конструкции
Задача 12. Расчет статически неопределимой фермы
Текст задания приведен на с. 21–22, схема конструкции выбирается по рис. 11, расположенному на с. 27. Подразумевается, что еще
перед решением задачи 4 (определение усилий в стержнях статически
определимой фермы) студент ознакомился с основными принципами и
методами расчета шарнирно-стержневых конструкций, включая способ вычисления перемещений их узлов (задача 7).
12.1. Расчетная схема. Её основой является схема фермы, предложенная для решения задачи 4 (см. с. 57), но теперь в каждую из четырех панелей, выделенных на приводимом ниже рисунке цветом, добавляется по одному стержню.
Такая ферма имеет четыре лишних связи, т. е. она четырежды
статически неопределима. Однако симметрия фермы сохранилась, а
ее опорные реакции по-прежнему определяются из уравнений равновесия. Их значения при действии прежней постоянной нагрузки остаются без изменения (см. задачу 4), что и отражено на изображенной
здесь расчетной схеме.
12.2. Основная система. Единичные и грузовые состояния. Основную систему следует выбрать симметричной, что позволит снизить
число основных неизвестных метода сил с четырех до двух. Именно
такая основная система и изображена в начале следующей страницы.
Она получается при разрезании четырех раскосов в центральных панелях и введением по направлению устраненных связей осевых сил X1
и X2 . Симметрично расположенные силы обозначены одинаково.
117
Задача 12
Единичные состояния фермы – это совокупности продольных сил,
возникающих в основной системе при воздействиях X1 = 1 и X2 = 1.
Симметрия конструкции позволяет ограничиться вычислением усилий
только в стержнях ее левой половины. Каждое из единичных воздействий самоуравновешено, поэтому реакции опор основной системы равны нулю как при нагружении X1 = 1, так и при воздействии
X2 = 1. В этом случае тут же обнаруживается (используются известные положения о нулевых стержнях фермы), что от нуля могут отличаться продольные силы только в стержнях той панели, которая
загружена самоуравновешенными силами Xi = 1. Для вычисления
ненулевых усилий используется метод вырезания узлов.
Сначала об усилиях, порождаемых силой
X1 = 1 при X2 = 0. Рассматривается только
вторая панель фермы при отброшенных нулевых стержнях. Необходимые для дальнейших вычислений значения тригонометрических функций указаны на расчетной схеме
фермы (см. с. 116).
Уравнения равновесия составляются для узла 2. Учитывается, что
N 9−10 = N 2−3 , N 3−10 = N 2−9 и N 3−9 = N 2−10 = 1. Таким образом,
Σx = 0 :
1 · sin α1 + N 2−3 = 0 → N 2−3 = N 9−10 = −0, 5039;
Σy = 0 :
1 · cos α1 + N 2−9 = 0 → N 2−9 = N 3−10 = −0, 8638;
N 3−9 = N 2−10 = 1.
Далее отыскиваются усилия в основной системе от воздействия
X2 = 1 при X1 = 0. Отличными от нуля будут усилия только в тех
118
Статически неопределимые конструкции
стержнях, которые принадлежат третьей панели. Рисунок этой панели, а также рисунки отделенных от нее узлов, предназначенные для
определения усилий, помещены ниже.
Узел 4
Σx = 0 :
Σy = 0 :
1 · sin α1 + N 3−4 = 0 → N 3−4 = −0, 5039;
1 · cos α1 + N 4−11 = 0 → N 4−11 = −0, 8638.
Узел 10
Σx = 0 : 1 · sin α1 +N 10−11 · cos α3 = 0 → N 10−11 = −
Σy = 0 :
0, 5039
= −0, 6192;
0, 8137
N 3−10 − N 1−10 · sin α3 + 1 · cos α1 = 0 →
N 3−10 = −0, 6192 · 0, 5812 − 0, 8638 = −1, 2237;
Узел 3
Σu = 0 : N 3−11 + N 3−4 · sin α2 + N 3−10 · cos α2 = 0 →
N 3−11 = 0, 5039 · 0, 3807 + 1, 2237 · 0, 9247 = 1, 3234.
Единичные состояния рассчитываемой конструкции установлены.
Теперь о грузовом состоянии. Принятая выше основная система
полностью совпадает с конструкцией, расчет которой на такое же точно воздействие был выполнен при решении задачи 4. Поэтому найденные ранее продольные силы (см. с. 58–60 и табл. 4.1 на с. 67) надлежит
рассматривать теперь как усилия, возникающие в основной системе
при действии на нее постоянной нагрузки.
119
Задача 12
12.3. Канонические уравнения. Система канонических уравнений
метода сил при n = 2 имеет вид:

u11 X1 + u12 X2 + U10 = 0, 
(12.1)
u21 X1 + u22 X2 + U20 = 0. 
В этих равенствах
uij =
X N ik N jk
(k)
EFk
Lk ,
Ui0 =
X N ik N0k
(k)
EFk
Lk .
(12.2)
Через k обозначен номер неопорного стержня. Суммы (12.2) берутся
по всем неопорным стержням левой половины фермы, при этом длина
стержня 4–11, находящегося на оси симметрии фермы, уменьшается
вдвое (см. задачу 7). Наконец, следует учесть, что осевые жесткости
всех неопорных стержней фермы одинаковы, а потому можно положить EFk = 1. В результате формулы (12.2) заменятся на соотношения:
X
X
uij =
N ik N jk Lk , Ui0 =
N ik N0k Lk .
(12.2a)
(k)
(k)
После решения системы (12.1) вычисляются усилия в стержнях
статически неопределимой фермы:
Nk = Nk0 + N 1k X1 + N 2k X2 .
(12.3)
12.4. Вычисления. Теперь можно обратиться к вычислениям, выполняемым в табличной форме. Приводимая на следующей странице
таблица 12.1 обрабатывается программой Excel. Столбцы A – E таблицы заполняются вручную. В столбец A заносятся номера стержней,
при этом номер 4–11 стержня, длина которого уменьшается вдвое, отмечается штрихом. В столбце B проставляются длины стержней. Наконец, в столбцы C, D и E последовательно заносятся усилия в стержнях основной системы, порождаемые соответственно воздействиями
X1 = 1, X2 = 1 и постоянной нагрузкой. Последние, как уже отмечалось, заимствуются из расчета, выполненного при решении задачи 4.
После этого в ячейки F4 – J4 вводятся команды, обеспечивающие
вычисление коэффициентов и свободных членов системы канонических уравнений по формулам (12.2a), а именно:
120
Статически неопределимые конструкции
121
Задача 12
=B4*C4*C4,
=B4*C4*D4,
=B4*D4*D4, =B4*C4*E4,
=B4*D4*E4.
Данные команды копируются в строки 5–18, что приводит к заполнению полей (F4:J4) таблицы. Чтобы прийти к численным значениям величин uij и Ui0 , надо в каждом из столбцов F – J сложить содержащиеся в них числа. Для этого в клетку F20 подается команда:
=СУММ(F4:F18), которая затем копируется в ячейки G20 – J20.
На этом заполнение столбцов таблицы временно приостанавливается, с тем чтобы решить систему канонических уравнений. Такое решение выполняется тут же, т. е. на том же самом листе программы Excel.
Используется метод исключения Гаусса, на реализацию которого выделяются строки 24–26 таблицы. Результаты решения содержатся в
полях L24 и M24.
Осталось выполнить заключительный этап расчета. В поле K4 записывается команда, реализующая вычисления по формуле (12.3):
=C4*$M$24+D4*$L$24+E4,
которая затем копируется в ячейки 5–18 столбца K.
И наконец, о столбцах L и M таблицы, предназначенных для контроля вычислений. Дело в том, что вектор усилий N , компоненты которого размещены в столбце K таблицы, при безошибочных вычислениях будет ортогональным к векторам N 1 и N 2 с компонентами,
находящимися соответственно в столбцах C и D. Сказанное означает,
что должны выполняться равенства:
X
(k)
Nk · N 1k · Lk = 0,
X
Nk · N 2k · Lk = 0.
(k)
Вычисление слагаемых в левых частях этих равенств как раз и выполняется в двух последних столбцах таблицы. И тот факт, что суммы этих слагаемых оказались равными нулю (см. ячейки L20 и M20)
свидетельствует о том, что задача решена правильно.
122
Статически неопределимые конструкции
Задача 13. Расчет плоской рамы смешанным методом
Текст задания приведен на с. 22–23, схема конструкции выбирается по рис. 11, расположенному на с. 27. Перед выполнением работы
следует по любому из литературных источников (учебнику, учебному пособию) познакомиться с основами расчета статически неопределимых конструкций смешанным методом. В пособии [1] необходимый
материал содержится на с. 512–519.
13.1 Предварительные замечания. Смешанный метод расчета статически неопределимых конструкций применяют в тех случаях, когда он приводит к меньшему числу неизвестных, чем при расчете методами сил и/или перемещений. Так, конструкции, изображенные на
рис. a, b и c целесообразно рассчитывать соответственно методами сил,
перемещением и смешанным. Этот вывод сделан на основе подсчета
числа неизвестных названных методов для всех трех конструкций.
Число неизвестных в методе перемещений велико для тех конструкций, которые состоят из ломаных стержней (рис. b), а также
имеют много междисковых шарниров. На число неизвестных метода
сил изломы осей стержней не влияют, а каждый шарнир даже снижает это число на единицу. Степень статической неопределимости конструкции тем выше, чем больше у нее бесшарнирных замкнутых контуров (рис. a). Поэтому если рама имеет вид, представленный на рис. c,
т. е. состоит из частей обоих описанных выше типов, ее расчет следует
вести смешанным методом. Конструкцию разбивают на две части. В
части I число неизвестных метода сил меньше, тогда как в части II
123
Задача 13
меньшим уже является количество неизвестных метода перемещений.
При выборе основной системы в I части конструкции связи устраняются, а во II – добавляются. Для рамы, показанной на рис. c, такой
прием (рис. d) позволяет снизить число неизвестных до четырех.
Таким образом, приступая к расчету смешанным методом, надо:
a) подсчитать числа неизвестных nсил и nпер методов сил и перемещений;
b) разбить конструкцию на части I и II и определить количество
nсм неизвестных смешанного метода;
c) если окажется, что nсм < nсил и nсм < nпер , то выполнить расчет
конструкции по излагаемой ниже схеме.
Выбор основной системы смешанного метода требует навыка, для
приобретения которого рекомендуем самостоятельно назначить основные системы для конструкций, изображенных на с. 125 (рис. 13.1).
Свои подсчеты и решения вы затем сможете сравнить с теми, что указаны на с. 129 (рис. 13.2). Что же касается схем рам, предлагаемых
для самостоятельного расчета, то их всегда можно разбить на части I
и II так, что основных неизвестных будет только два: nсм = 2.
13.2. Расчетная схема. Таковая изображается при помощи рис. 11 и табл. 8. Параметры конструкции и нагрузки на нее определяет шифр 843. Так как
ρ=
EIст
= 0, 2,
EIр
то можно положить EIст = EI, EIр = 5EI.
Нагрузка на конструкцию размещена в соответствии с указанием
к тексту задания.
13.3 Основная система. Для заданной рамы nсил = nпер = 3. При
разбиении конструкции на части I и II так, как это показано на рисунке, размещенном на следующей странице, получается, что nсм = 2.
Пусть J4 = EI/6, т. е. EI = 6. Тогда
J3 =
5·6
5EI
=
= 8, 57.
3, 5
3, 5
124
Статически неопределимые конструкции
Податливости стержней 1 и 2 таковы:
1
1
= ,
EI1
6
1
1
1
1
=
=
.
=
EI2
5EI
5·6
30
Приведенные податливости и приведенные погонные жесткости
элементов рамы указаны на основной системе рядом с соответствующими стержнями частей I и II конструкции.
Единичная эпюра "M 1 " строится от воздействия X1 = 1 в части I
основной системы, а во II ее части строится эпюра "M 2 " от перемещения Z2 = 1. Усилия M0 порождаются заданным внешним воздействием на основную систему. В подконструкции I их получают точно так
же, как и при расчете методом сил, т. е. способом сечений. В подконструкции II применяется подход, известный по методу перемещений,
– используются данные табл. 9.1, которая приведена на с. 96.
13.4. Формирование и решение системы канонических уравнений.
Система канонических уравнений смешанного метода при nсм = 2 такова:

u11 X1 + u∗12 Z2 + U10 = 0, 
(13.1)
∗ X +r Z +R

=
0.
r21
1
22 2
20
Перемещения u11 и U10 находят путем перемножения эпюр:
125
Задача 13
u11 = (M 1 , M 1 ) =
1
6
·
1
2
·2·2·
U10 = (M 1 , M0 ) =
1
30
·
1
2
2
3
·2+
1
30
· 2 · 5 · 2 = 1, 111;
· 2, 5 · 35 · 2 = 2, 917.
Для определения реакции r22 используется статический способ:
r22 = 4 + 25, 71 = 29, 71.
126
Статически неопределимые конструкции
∗ есть не что
Теперь о смешанных коэффициентах. Коэффициент r21
иное, как реактивный момент, который возникает во второй наложенной связи при воздействии X1 = 1. Как видно по рисунку основной
системы, это воздействие создает активный
момент R = 1 · 2 = 2 относительно узла с наложенной связью, направленный против хода часовой стрелки. Ясно, что реактивный
∗ )
момент указанной связи (т. е. момент r21
будет иметь противоположное направление,
которое совпадает с направлением перемещения Z2 . Сказанное объясняет, почему ве∗ берется положительной:
личина r21
∗
= 2.
r21
Смещение u∗12 по направлению первой устраненной связи, вызванное воздействием Z2 = 1, можно определить при помощи теоремы о
∗ . Согласно
взаимности единичных реакции и перемещения: u∗ik = −rki
этой теореме,
∗
= −2.
u∗12 = −r21
Однако ради надежности этот результат целесообразно получить и
непосредственно из геометрических рассмотрений. Ведь линейное перемещение u∗12 можно найти как произведение радиуса поворота ρ = 2
на угол поворота ϕ = 1 (ϕ = Z2 = 1):
u∗12 = −2 · 1 = −2.
Отрицательный знак здесь взят потому, что направления силы X1 = 1
и перемещения u∗12 противоположны.
Реакция R20 вычисляется статическим способом:
R20 = 35 − 6, 89 = 28, 11.
Из сказанного выше должно быть ясно, почему слагаемое 35 взято
положительным.
Подстановка в систему (13.1) вычисленных коэффициентов и свободных членов дает:
1, 111 X1 −

2 Z2 + 2, 917 = 0, 
2X1 + 29, 71 Z2 + 28, 11 = 0. 
(13.1a)
127
Задача 13
Отсюда следует (метод исключения неизвестных), что
X1 − 1, 800 Z2 + 2, 626 = 0,
X1 + 14, 855 Z2 + 14, 055 = 0;

(a) 
(b) 
(b) − (a) : 16, 665 Z2 + 11, 429 = 0 → Z2 = −0, 6862;
Из (a): X1 = −2, 626−1, 8 · 0, 6862 = −3, 861.
Чтобы проверить правильность решения системы (13.1a), образуют
суммарное уравнение
3, 111 X1 + 27, 71 Z2 + 31, 027 = 0,
складывая уравнения указанной системы. Подстановка в него величин X1 = −3, 861, Z2 = −0, 6862 приводит практически к тождеству:
−31, 026 + 31, 027 = 0, 001 ≈ 0. Канонические уравнения решены правильно и можно перейти к построению эпюр усилий: изгибающих моментов, поперечных и продольных сил.
13.5. Искомые усилия. Изгибающие моменты получают по уже знакомой по расчетным работам 5–7 формуле, вытекающей из принципа
наложения:
(13.2)
M = M0 + M 1 X1 + M 2 Z2 .
Приведенный выше рисунок иллюстрирует предусматриваемые
формулой (13.2) операции. По изображенной на нем эпюре "M " видно,
128
Статически неопределимые конструкции
что узлы рамы уравновешены по изгибающим моментам. Это является
одним из основных свидетельств правильности решения задачи. Приведенные рядом эпюры поперечных и продольных сил (эпюры "Q"
и "N ") построены по эпюре изгибающих моментов так, как об этом
говорилось при описании решения задачи 8.
В заключение рама изображается со всеми приложенными к ней
нагрузками (опорные реакции устанавливаются по эпюрам "M ", "Q"
и "N ") и делается проверка соблюдаемости условий равновесия конструкции в целом.
P
P
X = 0 : 3, 86 − 3, 17 − 0, 69 = 3, 86 − 3, 86 = 0,
Y = 0 : 14+4, 5 · 3, 5−0, 87−28, 88 = 29, 75−29, 75 = 0.
Задача 13
129
130
Статически неопределимые конструкции
Задача 14. Расчет плоской рамы на устойчивость
Текст задания приведен на с. 23–24. Схема конструкции дана на
рис. 11 – это схема рамы, рассчитанной методом перемещений на постоянную нагрузку при решении задачи 9. Теперь рама с теми же топологией, размерами и изгибными жесткостями стержней должна быть
рассчитана на устойчивость. Перед решением этой задачи необходимо
при помощи любого из литературных источников (учебника, учебного пособия) ознакомиться с основами расчета на устойчивость многостержневых конструкций. В пособии [1] нужный материал содержится
на с. 675–676 и 691–699.
14.1. Расчетная схема. Изображается при помощи рис. 11 и таблиц 6 и 9. Кроме того, следует посмотреть на расчетную схему этой
рамы, изображенную на с. 95. Там были указаны размеры элементов
рамы в метрах. Однако при расчете на устойчивость удобнее иметь
дело с относительными размерами стержней конструкции, что было
учтено при назначении расчетной схемы, которая приводится ниже.
Длина стержня 4 обозначена символом l, а длины остальных стержней
выражены через l с соблюдением пропорций, предписанных условиями задачи. Кроме того, исходными данными являются и продольные
силы в элементах рамы: предполагается, что расчет рамы на некое
статическое воздействие был выполнен заблаговременно, так что продольные силы в ней известны и могут быть записаны в виде N = ki qli ,
где i – номер стержня.
Коэффициенты ki выбираются из таблицы 9 (с. 24) по шифру 843.
В данном случае это величины: k1 = 21, k2 = 14, k3 = 3, k4+ = 9. Тогда
N1 = 21 · 1, 3ql, N2 = 14 · 1, 2ql, N3 = 3 · 1, 3ql, N4+ = 9 · 1, 3ql.
Знаки усилий не выписаны, ибо в последующие расчетные формулы
131
Задача 14
они не входят. Просто при сжатии используются одни формулы, а при
растяжении – другие (см. табл. 14.1 на с. 132). Согласно условию задачи, стержни 1–3 сжаты, а стержень 4 – растянут. На растянутый
стержень внимание обращается тем, что у всех связанных с ним величин, начиная с номера, проставляется значок "+" в виде верхнего
индекса. Однако на эпюре продольных сил, расположенном рядом с
расчетной схемой, знаки усилий проставлены.
14.2. Основная система. Единичные состояния. При расчете рам на
устойчивость целесообразно опираться на метод перемещений. Основная система ничем не отличается от той, что была назначена для рассматриваемой конструкции при решении задачи 9. Однако единичные
эпюры изменятся, ибо их теперь надо строить при помощи табл. 14.1,
приведенной на следующей странице.
Как видно из указанной таблицы,
q ординаты единичных эпюр зависят от некоторого параметра t = l P/EI, характеризующего осевую
силу в стержне и его жесткость при изгибе. Для каждого стержня это
будет своя величина. Если обозначить ql = P , то продольные силы в
стержнях можно будет записать следующим образом:
N1 = 27, 3P,
N2 = 16, 8P,
N3 = 3, 9P,
N4+ = 9P.
Понадобится еще одно переобозначение и одна перезапись:
ti = li
s
Ni
,
EIi
t=
s
P l2
,
EI
после которых можно перейти к вычислениям. Итак,
t1 = l1 ·
s
N1
= 1, 3
EI1
s
s
27, 3P l2
= 6, 7924
EI
P l2
= 6, 7924t,
EI
132
Статически неопределимые конструкции
t2 = l2 ·
s
t3 = l3 ·
N2
= 1, 2
EI2
s
t+
4 = l4 ·
s
N3
= 1, 3
EI3
s
N4
=
EI4
s
s
s
16, 8P l2
= 3, 1108
2, 5EI
s
3, 9P l2
= 1, 6237
2, 5EI
s
9P l2
= 1, 8974
2, 5EI
P l2
= 3, 1108t,
EI
P l2
= 1, 6237t,
EI
P l2
= 1, 8974t.
EI
Таким образом,
t1 = 6, 7924t, t2 = 3, 1108t, t3 = 1, 6237t, t+
4 = 3, 1108t.
(14.1)
133
Задача 14
Условные погонные жесткости элементов рамы назначены – они
указаны (в рамках) рядом с каждым стержнем изображенной на с. 131
основной системы. Поэтому ординаты всех трех единичных эпюр, построенных при помощи табл. 14.1, могут быть тут же вычислены. Само
построение осуществляется так, как об этом говорилось в п. 9.3, да и
внешне единичные эпюры метода перемещений в этой задаче и в задаче обычного статического расчета (задача 9) отличаются только тем,
что при обычном расчете они линейны, а при расчете на устойчивость
– криволинейны, что и отражено на приводимом ниже рисунке.
Нужно также обратить внимание на то, что у символов, входящих
в состав ординат единичных эпюр, имеются индексы, которые совпадают с номерами стержней основной системы.
14.3. Единичные реакции. Уравнение устойчивости. Коэффициенты системы канонических уравнений (единичные реакции) можно найти статическим способом, т. е. точно так же, как это было сделано при
решении задачи 9. Поэтому нижеследующие записи приводятся без
комментариев.
+
r11 = α1 + 2, 7083α 2 + 6, 5α+
4 , r12 = 6, 5β4 , r13 = −
r22 = 2α1 + 6, 5α+
4 + 2, 5α3 ,
r33 =
r23 = −
α1
α
= −0, 7692 1 ;
1, 3l
l
(α + β)1
2(α + β)1
= −1, 5385
;
1, 3l
l
γ1
γ
2γ1
γ
+
= 0, 5917 21 + 1, 1834 21 .
1, 69l2
1, 69l2
l
l
Из этих реакций составляется детерминант Det(P ), представляющий собой определитель системы канонических уравнений метода перемещений при решении задачи устойчивости. Уравнением устойчивости является соотношение Det(P ) = 0, в котором сила P представлена
134
Статически неопределимые конструкции
параметрами ti . Как видно из табл. 14.1, последние являются аргументами тригонометрических и гиперболических функций, а потому
уравнение Det(P ) = 0, которое по существу является уравнением вида
Det(t) = 0,
(a)
есть не что иное, как трансцендентное уравнение относительно параметра t (см. формулы (14.1)). Такое уравнение имеет бесконечное
множество корней, меньший из которых и определяет критическую
нагрузку.
В развернутом виде рассматриваемый определитель третьего порядка имеет представление:
2
2
2
−r22 ·r13
−r33 ·r12
,
Det(t) = r11 ·r22 ·r33 +2r12 ·r13 ·r23 −r11 ·r23
а потому более детальная запись равенства (a) такова:
2
2
2
−r22 ·r13
−r33 ·r12
= 0.
r11 ·r22 ·r33 +2r12 ·r13 ·r23 −r11 ·r23
(14.2)
Можно заметить, что при подстановке в уравнение (14.2) вычисленных ранее реакций rij , каждое слагаемое в левой части образовавшегося равенства будет содержать множитель 1/l2 . А так как в правой
части стоит нуль, то решение уравнения (14.2) не изменится, если указанный множитель заменить единицей. Но это означает, что и при
записи формул для реакций rij допустимо положить 1/l2 = 1. В этом
случае выражения для величин rij несколько упростятся:

+
r11 = α1 +2, 7083α 2 +6, 5α+

4 , r12 = 6, 5β4 , r13 = −0, 7692α 1 , 

r22 = 2α1 +6, 5α+
4 +2, 5α3 , r23 = −1, 5385(α + β)1 ,
r33 = 0, 5917γ 1 +1, 1834γ1 .

(14.3)




Из формул (14.3) видно, какие именно функции параметра t из тех,
что указаны в табл. 14.1, используются при решении уравнения (14.2).
В данном случае это функции:
+
α1 , α2 , α3 , α1 , α+
4 , γ1 , γ 1 , (α + β)1 , β4 .
Однако величины αi нельзя установить без предварительно найденных величин γi , поэтому указанный выше список необходимых для последующих вычислений функций следует расширить, включив в него
зависимости
γ 2 (t), γ 3 (t), γ4+ (t).
135
Задача 14
Теперь с помощью табл. 14.1 можно выписать все данные, необходимые
для решения уравнения устойчивости.
0, 5t31
γ t − sin t1
t31
γ1 =
, γ1 =
, β1 = 21 1
,
2tg(t1 /2) − t1
tg t1 − t1
t1 sin t1
2γ + t21
, α1 = (α + β)1 −β1 , α1 = γ 1 +t21 ;
(α + β)1 = 1
4
t32
t33
, α2 = γ 2 +t22 ; γ 3 =
, α3 = γ 3 +t23 ;
γ2 =
tg t2 − t2
tg t3 − t3
γ4+ =
γ + sh t4 − t4
0, 5t34
, β4+ = 42
,
t4 − 2th(t4 /2)
t4 sh t4
(α + β)+
4 =
2γ4+ − t24
+
+
, α+
4 = (α + β)4 − β4 .
4




















(14.4)



















14.4. Вычисления. Речь идет о нахождении первого положительного корня уравнения (14.2). Это можно сделать численно, наращивая
параметр t от нуля с некоторым шагом ∆t до тех пор, пока определитель Det(t) не сменит знак. Чтобы достичь желаемой точности, в
окрестности значения t∗ шаг ∆t дробят. Такие подсчеты однотипны,
поэтому их следует вести с использованием программы Excel. Последовательность выполнения операций такова.
1. По формулам (14.1) вычисляются значения параметров t1 – t4.
2. По формулам (14.4) находят значения функций γ1 (t) – α+
4 (t).
3. По формулам (14.3) вычисляются значения единичных реакций.
4. Вычисляется определитель Det(t), т. е. подсчитывается левая
часть уравнения (14.2).
При вычислении величины Det(t) с шагом ∆t = 0, 1, начинающимся при t0 = 0, обнаруживается, что смена положительного знака этого
определителя на отрицательный происходит на отрезке 0 < t < 0, 4.
Далее участок [0, 3 0, 4] оси t проходится с шагом ∆t = 0, 01, что позволяет сузить область определения корня tcr уравнения (14.2) до диапазона [0, 38 0, 39]. Продолжение уточнения границ искомого корня с
шагами ∆t = 0, 001 и ∆t = 0, 0001 приводит к результату
tcr = 0, 3488.
(14.5)
136
Статически неопределимые конструкции
Тогда (см. запись формул для параметров ti на с. 131–132)
tcr =
s
Pcr l2
t2 EI
EI
→ Pcr ≡ qlcr = cr 2 = 0, 1217 2 .
EI
l
l
Критическая нагрузка рамы установлена.
Как ясно из сказанного несколькими абзацами выше, вычисления выполняются при помощи программы Excel. Однако порождаемая проводимыми вычислениями таблица здесь не приводится. Представляется, что после примеров оформления электронных таблиц, рассмотренных выше (см. задачи 2, 6, 11), в этом уже нет необходимости.
Остается найти коэффициенты µi приведенных длин четырех сжатых стержней конструкции, для чего используется формула
µi =
π
,
µi
i = 1, 2, 3.
Так как при t = tcr (см. равенства (14.1) и (14.5))
t1 = 6, 7924 · tcr = 6, 7924 · 0, 3488 = 2, 3693,
t2 = 3, 1108 · tcr = 3, 1108 · 0, 3488 = 1, 0851,
t3 = 1, 6237 · tcr = 1, 6237 · 0, 3488 = 0, 5664.
Тогда
µ1 =
π
= 1, 3259;
2, 3693
µ2 =
π
= 2, 8951;
1, 0851
µ3 =
π
= 5, 5466.
0, 5664
Как известно, для защемленного с двух сторон сжатого стержня
µ = 0, 5. Более жесткое закрепление стержня по торцам (а потому и
более высокое сопротивление потере устойчивости) невозможно. Стало быть, коэффициент приведенной длины любого стержня рамы не
может быть меньше 1/2. Так оно при только что выполненном расчете
конструкции и получилось.
И еще одно важное замечание. Стойки рассчитанной рамы несколько отличаются друг от друга: левая стойка опёрта шарнирно, а правая
– защемлена, однако коэффициенты приведенной длины у них одинаковы. Объясняется это тем, что у стоек одинаковы не только длины и
изгибные жесткости, но и продольные силы, а значит – и параметры
137
Задача 14
нагружения t. Вот почему оказалось возможным назначить для стоек
рамы один общий номер. Будь продольные силы в стойках разные, им
пришлось бы дать разные номера.
14.5. Влияние растянутого стержня. При нагружении конструкции
в одних ее стержнях возникают сжимающие продольные силы, а в других – растягивающие. Последние оказывают стабилизирующее влияние на процесс потери устойчивости, т. е. приводят к увеличению
критической силы. Чем больше у конструкции растянутых стержней,
тем заметнее этот эффект. В рассматриваемой конструкции растянут
только один стержень, да и продольная сила в нем сравнительно невелика, так что рассчитывать на сколь-нибудь серьезное влияние этого
стержня на результат решения задачи не приходится. Однако любопытно проверить, насколько близко к истине сделанное предположение. Для этого расчет рамы на устойчивость следует повторить, положив N4 = 0. Новый расчет не так уж и обременителен, ибо вносимые
изменения в ранее использованные формулы несущественны, а потому незначительны изменения и таблицы программы Excel. Необходимые изменения вносятся в таблицу, заблаговременно скопированную
во второй лист созданного для основного расчета файла.
При N4 = 0 надо положить t4 = 0, что приведет к изменению первых
двух единичных эпюр: на стержне 4 это будут обычные эпюры метода
перемещений (см. задачу 9). Немного изменятся единичные реакции
r11 , r12 и r22 (см. формулы (14.3)):
r11 = α1 +2, 7083α 2 +13,
r12 = 6, 5,
r22 = 2α1 +13+2, 5α3 .
Все функции, помеченные ранее верхним индексом "+", теперь останутся без применения. Уравнение (14.2) не меняется, сохраняется и
вся последовательность вычислений. Результаты расчета таковы:
tcr = 0, 3487,
Pcr ≡ qlcr =
t2cr EI
EI
= 0, 1216 2 .
2
l
l
138
Статически неопределимые конструкции
Критическая сила уменьшилась всего на 0,07 %. Столь же незначительно меняются коэффициенты приведенных длин сжатых стержней:
µ1 = 1, 3264, µ2 = 2, 8961, µ3 = 5, 5485. Таким образом, высказанное
априори мнение о том, что в рассматриваемой задаче стабилизирующее влияние растянутого стержня окажется несущественным, более
чем подтвердилось.
Задача 15
139
Задача 15. Динамический расчет плоской рамы
Текст задания приведен на с. 24–26, схема конструкции изображена
на рис. 11. Перед решением задачи следует ознакомиться с основами
расчета стержневых систем с конечным числом степеней свободы на
гармоническое динамическое воздействие, а также с теорией собственных колебаний таких систем. В частности, необходимый материал по
теме задания можно найти в пособии [1] на с. 601–606 и 618–621.
15.1. Расчетная схема. Образуется при помощи рис. 11 и табл. 10.
Изображенная ниже расчетная схема выполнена в строгом соответствии с указаниями, приведенными на с. 26. Рядом с расчетной схемой
указаны исходные данные, взятые из табл. 10 по шифру 843, которые
потребуются при дальнейших вычислениях.
Коэффициенты ki , определяющие длины стержней по их номерам i, таковы: k1 = 1, 7, k2 = 3, 2, k3 = 1, 5, k4 = 1, 9. Коэффициент k,
показывающий во сколько раз изгибная жесткость ригеля выше изгибной жесткости стойки, равен 1,2.
Важнейшим фактором, определяющим ход расчета конструкции
на динамическое воздействие, является число ее степеней свободы, т. е.
число независимых кинематических параметров, полностью определяющих движения масс. В данной задаче масса только одна, но двигаться она может в плоскости, к которой отнесена расчетная схема, в
любом направлении. Вектор перемещения точки сосредоточения масс
140
Статически неопределимые конструкции
допустимо разложить на две составляющие, а потому рассматриваемая динамическая система имеет две степени свободы. Направления,
по котором раскладывается указанный вектор перемещения, показаны
на рисунке, помещенном выше, под номерами 1 и 2.
15.2. Собственные колебания конструкции. Расчету конструкции
на любое динамическое воздействие предшествует исследование собственных колебаний системы. Прежде всего вычисляются частоты ωi
таких колебаний: в данном случае это собственные частоты ω1 и ω2 .
Они связаны с параметрами λ1 и λ2 равенством
ωi2 = 1/λi ,
i = 1, 2.
(15.1)
В свою очередь величины λ1 и λ2 при m1 = m2 = m находят как корни
некоторого квадратного уравнения, т. е. по формуле:
λ1, 2 = 0, 5m[u11 + u22 ±
q
(u11 − u22 )2 + 4u212 ].
(15.2)
В этой формуле uij – перемещения точки сосредоточения массы вдоль
линий (1) и (2), вызванные единичными силами, также направленными вдоль этих линий. Другими словами, u11 и u21 – это перемещения
по указанным направлениям от воздействия P1 = 1, а u12 и u22 – перемещения по тем же самым направлениям, но уже при действии силы
P2 = 1. По теореме взаимности единичных перемещений u12 = u21 . Величины uij находят перемножением эпюр, т. е. по правилам, о которых
шла речь при решении задачи 5.
Прежде всего следует построить эпюры изгибающих моментов в заданной статически неопределимой раме от действия сил P1 = 1 и P2 = 1.
Это можно сделать, опираясь на метод перемещений. Но поскольку
расчет стержневых конструкций методом перемещений на фиксированное воздействие уже отработан (задача 9), то можно сэкономить
время и получить требуемые эпюры при помощи любой программы,
предназначенной для расчета стержневых конструкций. В частности,
удобно воспользоваться программой ПОЛЮС. Именно при помощи
этой программы и построены эпюры усилий M1 и M2 , изображенные
на рисунке, который приведен ниже. Программа ПОЛЮС позволяет
найти и перемещения uij , однако этим обстоятельством следует воспользоваться лишь для контроля вычислений. Тем более что непосредственный подсчет указанных перемещений в статически неопределимых конструкциях можно вести по формуле uij = (Mi , Mjсил ), где Mjсил
141
Задача 15
– эпюра изгибающих моментов, построенная в любой основной системе метода сил. Это обстоятельство существенно упрощает вычисления,
так как при разумном выборе основной системы эпюра Mjсил получается локальной, занимающей малую часть осевого контура конструкции.
Такие эпюры также приведены на расположенном ниже рисунке.
При вычислении перемещений используется прием разложения сложных эпюр изгибающих моментов на простые фигуры.
Итак,
u11 = (M1 , M1сил ) =
2ω · mсил − ωсил · m
1 h 1
2
2· ·1, 6l·0, 8l· ·0, 8l−
=
1, 2EI
1, 2EI
2
3
i
1
l3
1
;
− · 3, 2l · 0, 8l · (0, 315236l + 0, 301187l) = 0, 240116
2
2
EI
142
Статически неопределимые конструкции
u12 = (M2 , M1сил ) =
ωсил · m 0, 5 · 3, 2l · 0, 8l · 0, 106197
l3
=
= 0, 113277
;
1, 2EI
1, 2EI
EI
u22 = (M2 , M2сил ) =
ωсил · m
=
EI
2
l3
1
1 1
1, 9l · 1, 9l
1, 075008 − 0, 824992 = 0, 797225
.
EI 2
3
3
EI
Таким образом,
=
u11 = 0, 240116
l3
,
EI
u12 = 0, 113277
l3
,
EI
u22 = 0, 797225
l3
, (15.3)
EI
и теперь можно приступать к вычислениям по формуле (15.2). Так как
u11 + u22 = 1, 037341 l3 /EI, u11 − u22 = −0, 557110 l3 /EI, то
λ1, 2 = 0, 5m[1, 037341 ±
q
0, 5571102 + 4 · 0, 1132772 l3 /EI],
откуда следует, что λ1, 2 = ml3 (1, 03734 ± 0, 601413)/2EI и
λ1 = 0, 819377 ml3 /EI,
λ2 = 0, 217964 ml3 /EI.
(15.4)
Тогда (см. формулы (15.1))
ω12 = 1, 220440
EI
,
ml3
ω22 = 4, 587917
EI
.
ml3
(15.5)
Пусть Aij – амплитудное перемещение массы m по направлению
i = 1, 2 при частоте колебаний ωj (j = 1, 2). Между амплитудами A1j
и A2j существует связь вида: A2j = ρA1j , где (см. формулы (15.3))
ρj ≡
λj EI/ml3 − 0, 240116
λj − mu11
.
=
mu12
0, 113277
При частотных параметрах λj , определяемых равенствами (15.4), множители ρj будут следующими:
ρ1 =
0, 217964−0, 240116
0, 819377−0, 240116
= 5, 113680; ρ2 =
= −0, 195554.
0, 113270
0, 113270
143
Задача 15
Эти равенства означают, что при перемещении массы в направлении (1) на единицу, перемещение той же массы в направлении (2)
оказывается равным величине ρj . Собственные векторы
e1 = [1 ρ1 ] = [1 5, 113680],
e2 = [1 ρ2 ] = [1 − 0, 195554]
определяют формы свободных колебаний с частотами ω1 и ω2 соответственно. При m1 = m2 = m эти векторы должны быть ортогональными,
т. е. должно выполняться условие ρ1 · ρ2 = −1. И в самом деле,
5, 113680 · (−0, 195554) = −1.
Собственные формы колебаний конструкции, диктуемые векторами e1
и e1 , приведены на располагаемом ниже рисунке.
15.3. Характеристики двигателя. Возмущающая сила. Необходимые данные о двигателе – масса ротора, смещение центра массы последнего относительно центра вращения и круговая частота вращения ротора определены условиями задачи. Эти величины указаны на рисунке.
По ним вычисляется центробежная сила
Q, возникающая при вращении ротора, а
затем – и возмущающие силы Q sin θ и
Q cos θ, действующие на раму.
Итак,
Q=
(θe)2
mrot v 2
= mrot ·
= θ 2 · 0, 26m · 1, 5 · 10−3 l = 3, 9 · 10−4 θ 2 ml,
e
e
где (см. формулы (15.5))
θ 2 = 0, 49 ω12 = 0, 49 · 1, 220440 EI/ml3 = 0, 598015 EI/ml3 .
144
Статически неопределимые конструкции
Таким образом,
θ 2 = 0, 598015
EI
,
ml3
Q = 3, 9 · 10−4 θ 2 ml = 2, 332260 · 10−4
EI
. (15.6)
l2
15.4. Амплитуды вынужденных колебаний. Амплитуды C1 и C2 колебаний масс m1 и m2 при m1 = m2 = m определяются следующей
системой уравнений:
(1 − u11 m θ 2 )C1 − u12 m θ 2 C2 = u10 Q,
− u21 m θ 2 C1 + (1 − u22 m θ 2 )C2 = u20 Q.
)
В эти соотношения подставляется сила Q, определяемая соответствующей формулой из равенств (15.6), после чего уравнения для амплитуд
приводятся к виду:
(1/m θ 2 − u11 )C1 − u12 C2 = 3, 9 · 10−4 l u10 ,
− u21 C1 + (1/m θ 2 − u22 )C2 = 3, 9 · 10−4 l u20 .
)
Перемещения uij даются формулами (15.3), а для величины θ 2 имеется
запись (15.6). Если подставить эти зависимости в уравнения для амплитуд и выполнить элементарные подсчеты, то получится следующая
система линейных алгебраических уравнений, полностью определяющая динамические перемещения C1 и C2 :
1, 432082 C1 − 0, 113277 C2 = 3, 9 · 10−4 · (EI/l2 ) · u10 ,
− 0, 113277 C1 + 0, 874973 C2 = 3, 9 · 10−4 · (EI/l2 ) · u20 .
)
(15.7)
Для решения этой системы используется правило Крамера, требующее
вычисление определителя D данной системы:
D = 1, 432082 · 0, 874973 − (−0, 113277)2 = 1, 240201,
а также определителей
EI
D1 = 3, 9·10−4 2
l
Таким образом,
u
10
u20
−0, 113
0, 874
EI
, D2 = 3, 9·10−4 2
l
1, 432
−0, 113
u10
u20
EI
D1 = 3, 9 · 10−4 (0, 874973 u10 + 0, 113277 u20 ) 2 ;
l
EI
−4
D2 = 3, 9 · 10 (0, 113277 u10 + 1, 432082 u20 ) 2 .
l
D = 1, 240201;
.
145
Задача 15
Следовательно,
D1
EI
= 3, 562161 · 10−5 (7, 724199 u10 + u20 ) 2 ;
D
l
D2
EI
−5
C2 =
= 3, 562161 · 10 (u10 + 12, 642326 u20 ) 2 .
D
l
C1 =
(15.8)
Формулы (15.8) содержат перемещения u10 и u20 точки сосредоточения массы по направлениям (1) и (2), вызванные возмущающей
силой Q = 1. Эта центробежная сила постоянно меняет свое направление. Интерес представляют такие направления, при которых расчетные усилия принимают экстремальные значения. Оказывается, что
для определения экстремальных усилий вовсе не обязательно знать те
моменты времени, в которые такие усилия реализуются. Достаточно
найти значения расчетных усилий при вертикальном направлении силы Q = 1, а также при горизонтальном направлении этой силы. О действии центробежной силы по названным направлениям говорят как о
вертикальном и горизонтальном толчках двигателя.
Как видно из расположенного выше рисунка (см. также формулы
(15.3) на с. 142), при вертикальном толчке двигателя следует положить
u10 = u11 = 0, 240116 l3 /EI, u20 = u12 = 0, 113277 l3 /EI и установить по
формулам (15.8), что
C1V = 0, 701025 · 10−4 l,
C2V = 0, 595664 · 10−4 l.
(15.9a)
Если же толчок двигателя горизонтален, то u10 = u12 = 0, 113277 l3 /EI,
u20 = u22 = 0, 797225 l3 /EI и, согласно формулам (15.8),
C1H = 0, 595664 · 10−4 l,
C2H = 3, 630574 · 10−4 l.
(15.9b)
Выполнение равенства C2V = C1H является подтверждением правильности вычислений.
146
Статически неопределимые конструкции
15.5. Огибающая эпюра изгибающих моментов. Ординатами этой
эпюры являются экстремальные значения изгибающих моментов в расчетных сечениях рамы, возникающие при действии постоянной нагрузки P = mg и сил инерции. Амплитудные значения Pi = mi θ 2 Ci последних вычисляются в данной задаче при mi = m с учетом того, что (см.
первую из формул (15.6) на с. 144)
m θ 2 = 0, 598015 EI/l3 .
Амплитудные значения перемещений при вертикальном толчке двигателя даются формулами (15.9a). Стало быть,
P1V = (m θ 2 ) · C1V = 0, 598015
EI
EI
· 0, 701025 · 10−4 l = 0, 419224 · 10−4 2 ,
3
l
l
EI
EI
· 0, 595664 · 10−4 l = 0, 356216 · 10−4 2 .
3
l
l
Если же толчок двигателя горизонтален, то используются формулы
(15.9b). Тогда
P2V = (m θ 2 ) · C2V = 0, 598015
P1H = (m θ 2 ) · C1V = 0, 598015
EI
EI
· 0, 59664 · 10−4 l = 0, 356216 · 10−4 2 ,
3
l
l
EI
EI
· 3, 630574 · 10−4 l = 2, 171139 · 10−4 2 .
3
l
l
Теперь можно приступить к построению эпюр изгибающих моментов. Эпюра "M 0 " строится от постоянной нагрузки, т. е. от силы
P = mg, приложенной вертикально вниз в точке сосредоточения массы.
Но от подобной нагрузки, а именно – от воздействия P = 1 уже была
построена эпюра изгибающих моментов в рассматриваемой раме. Речь
идет об эпюре "M1" , изображенной на с. 141. Значит, ординаты эпюры
усилий M 0 будут отличаться от соответствующих ординат эпюры усилий M1 только множителем mg. Сказанное здесь как раз и отражено
на рисунке, помещенном ниже.
P2H = (m θ 2 ) · C2V = 0, 598015
147
Задача 15
Следует обратить внимание на то, в каком виде записаны ординаты
на эпюре "M 0 ". Дело в том, что промежуточные подсчеты необходимо выполнять с достаточно высокой точностью, чтобы свести к минимуму последствия накопления вычислительной погрешности1 . Это
обcтоятельство подчеркивалось тем, что при записи чисел в ходе предварительных вычислений указывались шесть цифр после запятой, тогда как значения результирующих усилий указываются в сокращенной
форме.
Далее выполняется построение эпюр изгибающих моментов от динамических воздействий. К последним относятся возмущающая сила
Q и силы инерции PiV , PiH . Формулы для динамических воздействий
приведены на с. 144 (формула (15.6)) и с. 146. В записи этих величин
присутствует множитель
EI/l2 = 16000 кНм 2 /1 м2 = 16000 кН,
учитывая который можно указать численные значения всех динамических сил:
Q = 2, 332260 · 10−4 · 16000 кН = 3, 731616 кН,
P1V = 0, 419224 · 10−4 · 16000 кН = 0, 670758 кН,
P2V = P1H = 0, 356216 · 10−4 · 16000 кН = 0, 569946 кН,
P2H = 2, 171139 · 10−4 · 16000 кН = 3, 473823 кН.
Сначала рассматривается случай, когда усилия в раме возникают
при вертикальном толчке двигателя. Действуют направленная вниз
сила Q и порождаемые ею силы инерции P1V и P2V . Ясно, что можно найти усилия от этих воздействий по отдельности, а затем сложить
результаты. Поскольку изгибающие моменты M1 и M2 от соответствующих единичных воздействий были найдены еще в п. 15.2, то при
построении искомой динамической эпюры "MV " можно опереться на
формулу
M V = (Q + P1V )M1 + P2 M2 .
Эта формула напоминает зависимости, которые используются при вычислении изгибающих моментов в статически неопределимых системах в случаях, когда расчет выполняется методами сил, перемещений
1
Впрочем, Excel требуемую точность вычислений заведомо обеспечивает.
148
Статически неопределимые конструкции
и смешанным. Поскольку порядок действий в этих случаях был подробно рассмотрен при рассмотрении задач 8, 9 и 13, здесь можно
ограничиться только окончательным результатом. Он и представлен
на расположенном ниже рисунке.
Совершенно аналогично строится вторая динамическая эпюра, относящаяся к случаю горизонтального толчка двигателя. Для ее построения используется зависимость
M H = P1H M1 + (Q + P2H )M2 .
Значения Mдин экстремальных изгибающих моментов, обусловленных динамическим воздействием, находят по формуле
Mдин =
q
(M V )2 + (M H )2 .
(15.10)
Речь идет о вычислении характерных ординат эпюры усилий Mдин ,
изображенной ниже.
149
Задача 15
На данном рисунке ординаты отложены с той стороны, с которой
значения усилий на эпюрах ”M V ” и ”M H ” больше по модулю. Видно,
что узел рамы, в котором сходятся три стержня, не уравновешен по
изгибающим моментам. Это и понятно, ибо использование "нелинейной" формулы (15.10) для вычисления ординат динамической эпюры
усилий приводит к нарушению принципа наложения.
Ясно также, что при колебаниях системы меняются не только значения динамических сил, но и их направления. Поэтому в состоянии,
противоположном по фазе тому состоянию, которому отвечает изображенная выше эпюра "Mдин ", знаки всех ординат сменятся на противоположные. Вот почему динамический расчет конструкции завершается построением огибающей эпюры изгибающих моментов "Mог ".
Ординаты последней вычисляют по формулам:
max Mог = M 0 + Mдин ,
min Mог = M 0 − Mдин .
Через M 0 обозначены усилия, возникающие при действии постоянной
нагрузки. Эпюра этих усилий приведена на с. 146.
Узлы рамы по огибающим изгибающим моментам уравновешены,
так как неравновесные части входят в ее состав с противоположными
знаками и компенсируют друг друга.
15.6. Число оборотов двигателя. Техническая частота вращения
ротора, т. е. число его оборотов в минуту, дается формулой n = 30 θ/π.
Используя первую из формул (15.6) и исходные данные к решению
рассматриваемой задачи, нетрудно установить, что
EI
16000g
16000 · 9, 81
=
= 5214, 69.
θ 2 = 0, 598015 3 = 0, 598015 3
ml
l mg
18 · 13
q
Стало быть, n = 30 · 5214, 69/π = 689, 64 об/мин. Следует выбрать
двигатель с характеристикой n = 700 об/мин.
ЧАСТЬ IV. РАСЧЕТ КОНСТРУКЦИЙ С ПОМОЩЬЮ
ПРОГРАММЫ ЛИРА
Задача 16. Расчет трехшарнирной арки
На практике расчет несущих конструкций выполняется, как правило, при помощи мощных программ, специально для этой цели предназначенных. Только небольшие частные расчеты ведутся, как говорится, вручную, с обращениям, например, к таким вычислительным
средствам, как электронные таблицы. Сказанное может породить иллюзию, что изучение методов расчета, о которых шла речь в предыдущих частях пособия, лишается смысла: ведь специальные программы
позволяют достаточно быстро решать задачи практически любой степени сложности, а с простыми задачами справляются мгновенно. Все
это так, но тогда почему для решения задач, требующих обращения к
специальным программам, привлекаются только такие инженеры, которые в совершенстве владеют методами вычислений, описанными в
предыдущих частях пособия? Ответ прост – никому другому оценить
полученные результаты машинного расчета не удастся. Достаточно допустить небольшую неточность при задании исходных данных, несущественно ошибиться в формировании расчетной схемы, неудачно выбрать траекторию расчета, чтобы получить в итоге неверную информацию об усилиях, напряжениях и перемещениях в конструкции. Как
же выяснить, заслуживают ли доверия полученные результаты или
нет, а если они ошибочны, то как понять, где была допущена ошибка
и что надо сделать для того, чтобы ее исправить? Вот почему любой
результат расчета должен быть тщательно проанализирован. Сделать
это может только высококвалифицированный специалист, владеющий
простыми методами получения оценочных решений. Да и рассказывать об использовании промышленных программ расчета силовых конструкций тому, кто обычных методов расчета таких конструкций не
знает, бессмысленно. Читателю это станет ясным сразу же, как он
приступит к изучению настоящего раздела.
Все специальные программы обсуждаемого типа, в том числе и
программа ЛИРА, основаны на методе конечных элементов. Начальные сведения об этом методе можно получить при помощи пособия [1]
(с. 555–578).
Задача 16
151
16.1. О программе ЛИРА. Эта программа предназначена для численного расчета произвольных строительных конструкций на любые
воздействия, встречающиеся в инженерной практике. В частности, с
ее помощью можно находить усилия, напряжения и перемещения в
любых стержневых конструкциях. Расчетный модуль программы базируется на методе конечных элементов, идеологически близком к
методу перемещений. Элементами моделей рассчитываемых объектов
(расчетных схем) могут служить точки, стержни, пластины, оболочки, массивные тела. Имеется возможность решать геометрически и
физически нелинейные задачи.
Как уже отмечалось, ЛИРА ориентирована на выполнение расчетов для строительной отрасли, а потому специфические для строительных конструкций воздействия, их расчетные сочетания, информация о жесткостных характеристиках элементов задаются намного
проще, чем при использовании программ общего назначения. ЛИРА
имеет специальные конструкторские модули, позволяющие, например,
выполнить подбор поперечного сечения, в состав которого входят стандартные прокатные профили, или подобрать арматуру железобетонного элемента. Разумеется, если решается задача, которая не требует обращения к строительным нормам, пользователь может игнорировать
специфические возможности программы. Так обычно и поступают при
решении учебных задач и задач исследовательского характера.
Следует обратить внимание на то обстоятельство, что расчетная
модель метода конечных элементов отличается от расчетной модели
строительной механики стержневых систем. Основу второй из указанных моделей составляют узел и стержень, а основу первой – узел и конечный элемент. И тут дело не только в том, что конечный элемент не
обязательно должен быть стержневым, а то, что и сам стержень может
быть представлен в модели набором как стержневых, так и нестержневых конечных элементов. Да и узел трактуется в сопоставляемых
моделях по-разному.
Узел – это объект, не имеющий размеров. Он представляет собой
точку, но точку специфическую. Так, точка, являющаяся простым геометрическим объектом, задается своими координатами и только. Узел
же может быть, например, наделен массой, так что его характеризуют
как координаты, так и величина точечной массы. Другими словами,
узел в методе конечных элементов – физический объект, а не геомет-
152
Расчет с помощью программы ЛИРА
рический. Кроме того, в отдельных случаях метод конечных элементов допускает использование изолированных узлов, которые никак не
связаны с другими элементами модели.
Конечный элемент – это подконструкция, которая представляет
собой тело простой формы. Для каждой программы набор таких тел,
называемый библиотекой конечных элементов, определяется ее (программы) разработчиками. Библиотека конечных элементов содержит
набор примитивов, с помощью которых расчетчик формирует свою
модель. Типичными являются следующие конечные элементы:
1) точечные элементы;
2) стержневые призматические элементы различных типов: испытывающие только осевую деформацию, испытывающие изгиб и сдвиг
в одной плоскости, испытывающие кручение, а также изгиб и сдвиг в
двух плоскостях;
3) пластинчатые треугольные и четырехугольные элементы, используемые для моделирования плит и оболочек;
4) Объемные элементы в форме тетраэдра (4 грани) и гексаэдра
(6 граней).
Совокупность узлов и конечных элементов называется конечноэлементной сеткой. При этом элементы соединяются друг с другом только
при помощи узлов. Соединения по граням пластинчатых и объемных
конечных элементов отсутствуют, даже если эти грани вплотную примыкают друг к другу. Последовательность задания конструкции и ее
последующего расчета такова. Сначала генерируется конечноэлементная сетка, что требует, как правило, точной и кропотливой работы,
которая, к тому же, может быть выполнена разными способами. Затем
на опорные узлы конструкции накладываются связи. На следующем
этапе расчета задается нагрузка, которая может быть отнесена как к
узлам, так и к конечным элементам. Необходимо также указать материал конструкции и геометрические характеристики поперечных сечений элементов. Для стержневых элементов возможно непосредственное задание жесткостей – осевой, изгибной и т. д. Остается выполнить
вычисления, сохранить и осмыслить полученные результаты.
Описанная последовательность операций не является жесткой, так
как на каждом шаге можно вернуться назад и внести коррективы в
исходную схему.
Задача 16
153
Выполняя расчет конструкции, важно понимать, что приходится
оперировать минимум с двумя системами координат – глобальной (общей) и локальной (местной). В первой из них указываются координаты узлов, в ней же могут быть заданы связи и нагрузки. Найденные
в результате расчета перемещения узлов также отнесены к глобальному базису. С каждым конечным элементом связана своя локальная
система координат, в которой вычисляются усилия и напряжения.
16.2. Об интерфейсе программы ЛИРА. Программа запускается по
команде Пуск/Программы/Lira Soft/ЛИРА 9.6/ЛИРА 9.6. Если с данной установкой программы уже работали, то загрузится уже введенная предыдущим пользователем расчетная схема. Её можно удалить
командой Файл/Закрыть и создать свой файл: Файл/Новый. В результате появится окно Признак схемы, содержащее ряд полей для
заполнения. Правда, поля «Имя задачи», «Шифр задачи», «Описание
задачи»... могут быть проигнорированы, так как вносимая в них информация нужна лишь для последующей идентификации решаемой
задачи. А вот выбор одного из предлагаемых признаков схемы обязателен. При расчете плоской стержневой изгибаемой конструкции выбирается признак 2: 2 - Три степени свободы в узле (два перемещения
и поворот) XOZ. Следует подчеркнуть, что плоская стержневая конструкция всегда соотносится с плоскостью XOZ глобального базиса.
Режим задания исходных данных включается командой Применить. Эта команда, как и почти все другие, может быть подана из
меню, расположенного в верхней части окна программы, так и по нажатию кнопки, находящейся в верхней панели инструментов. Первый
способ более осмысленный, второй – более простой. Чтобы и вторым
способом пользоваться с пониманием сути дела, надо знать функции
каждой кнопки. В приводимой на странице 155 таблице 16.1 эти функции указаны. Кроме того, в таблице всем кнопкам приданы номера,
заключенные в угловые скобки, что упрощает в дальнейшем ссылки
на отдаваемые команды.
В центральной части окна находится рабочая область экрана, в которой отображается конструкция. В левом нижнем углу приведен рисунок, указывающий на направление осей глобального базиса (но не
начало общей системы координат). По умолчанию схема конструкции
отображается в аксонометрической проекции. Традиционные элементы управления – меню и панель инструментов – будут обсуждаться
154
Расчет с помощью программы ЛИРА
по ходу решения конкретных задач, а пока имеет смысл разобраться
в функциях отдельных подменю.
1. Подменю Файл – предназначено для выполнения операций с
файлами.
2. Подменю Режим – предназначено для переход от задания исходных данных к просмотру результатов и обратно.
3. Подменю Вид – предназначено для отображения различных типов конструкции.
4. Подменю Выбор – предназначено для выделения узлов и конечных элементов, чтобы позволить выполнить требуемые операции над
ними.
5. Подменю Схема – предназначено для ввода и корректировки
исходных данных.
6. Подменю Жесткости – применительно к стержням предназначено для задания размеров и формы поперечных сечений, материала,
либо задания относительных жесткостей конечных элементов.
7. Подменю Нагрузки – предназначено для задания и корректировки внешних воздействий на узлы и конечные элементы.
8. Подменю Опции – предназначено для ряда настроек среды (например, выбор единиц измерения, выбор выводимых на экран результатов расчета и т. п.).
9. Подменю Окно – предназначено для отображения различных
окон, в том числе окон с таблицами исходными данных и результатов
расчета.
10. Подменю ? – содержит справочные данные. В этом разделе особый интерес представляют обучающие примеры.
В правой части экрана должен быть расположен так называемый
графический контейнер (вытянут по вертикали). Если это не так, то
обсуждаемый объект включается по команде Окно/Графический контейнер. В него (контейнер) можно сначала скопировать содержимое
рабочей области (т. е. конечноэлементную сетку), для чего используется кнопка <18>1 , а затем щелчком правой кнопки мыши получить
уменьшенную копию изображения и сохранить его в любом растровом
формате. Желательно также периодически сохранять и сами исходные
1
И далее помещенное за именем команды в угловых скобках число будет являться номером кнопки по табл. 16.1, нажатие на которую обеспечивает вызов
требуемой команды.
Задача 16
155
данные, особенно перед расчетом (<1>). При этом сохранение можно
выполнять в любом каталоге, а не только в предлагаемом программой по умолчанию. В результате будет создан файл с расширением
lir. Если этот файл перенести на другой компьютер с установленной
программой ЛИРА, то и расчет конструкции можно будет на новом
компьютере довести до конца.
156
Расчет с помощью программы ЛИРА
И еще одно обстоятельство. В предыдущем абзаце говорилось о
команде, подаваемой щелчком правой кнопки мыши. Это почти единственное исключение из общего правила для ЛИРЫ – любые операции выполнять нажатием левой кнопки мыши. Поэтому в дальнейшем
прилагательное перед словами «кнопки мыши» опускается.
16.3. Исходная информация к расчету трехшарнирной арки. Речь
идет о конструкции, расчет которой на постоянную нагрузку был выполнен при решении задачи 2 (см. с. 38–49). Представляется интересным повторить вычисления с помощью программы ЛИРА и сравнить
результаты.
Прежде всего создается конечноэлементная сетка, для чего используется расчетная схема конструкции, предложенная на с. 40. Поскольку в библиотеке ЛИРЫ, как и в библиотеках большинства других
подобных программ, непризматические стержневые элементы отсутствуют, ось арки придется заменить вписанной ломаной линией. Это
означает, что решение задачи окажется приближенным, а потому неизбежен последующий анализ сходимости полученных результатов.
Приступая к созданию сетки, надо убедиться, что используются
требуемые единицы измерения. Если это не так, их нужно установить
с помощью подменю Опции. На вкладке Схема для линейных размеров назначаются метры, для сил – килоньютоны. Такие же единицы измерений назначаются и на вкладке Результаты. Затем требуется открыть диалоговое окно Добавить узел, чего можно добиться с
помощью команды Схема/Корректировка/Добавить узел<17>. После
этого выполняется переход на вкладку Формульный ввод.
В поле ввода справа от символов Y = задается выражение, описывающее очертание арки. В качестве независимой переменной указывается x. Используются традиционные знаки арифметических операций: ∗ – умножение, ˆ – возведение в степень, / – деление, а также
обозначения для ряда часто встречающихся функций, перечень которых приведен в справке. Аргументы функций обязательно заключены
в круглые скобки. При вводе чисел в качестве десятичного разделителя всегда используется точка.
В рассматриваемом примере ось арки состоит из двух сопряженных в замковом шарнире кубических парабол (см. с. 41). Сначала вво-
157
Задача 16
дится формула, определяющая левую часть оси:
8/26 ∗ x ∗ (3 − 4 ∗ (x/26)2 ).
Указываются плоскость XOZ, к которой отнесена рассматриваемая
полуарка, число n конечных элементов, на которое последняя разбивается (принято n = 8), а также значения 0 и 13 для граничных абсцисс
X1 и X2 аргумента x. Параметр n определяет точность геометрического представления кривой. Число узлов n+1 = 9 выбрано для наиболее адекватного сравнения результатов расчета, выполненного при
решении задачи 2, с результатами, которые будут получены с использованием программы Лира.
Создавая сетку, надо следить за тем, чтобы в диалоговом окне слева от условного изображения стержня стояла галочка: при ее отсутствии узлы не будут на рисунке соединены между собой. После завершения набора данных дается команда Применить<35>*, что приводит
к появлению на экране изображения конечноэлементной сетки. Если
полученная картина удовлетворяет пользователя, то это окно можно закрыть. Если же требуются коррективы, то надо воспользоваться
командой Отмена<10> и, не выходя из режима диалога, внести необходимые изменения.
158
Расчет с помощью программы ЛИРА
В итоге полуось арки заменяется ломаной, которая состоит из отрезков разной длины, причем проекции этих отрезков на ось X одинаковы.
Далее формируется конечноэлементная сетка правой части конструкции. Для этого нужно уже созданную сетку скопировать и отразить относительно плоскости, параллельной плоскости Y OZ. Это
можно сделать, включив режим отметки узлов: Выбор/Отметка узлов<8> и режим отметки элементов Выбор/Отметка элементов<9>.
Все объекты выделяются одновременно при нажатой кнопке мыши с
помощью "резиновой" рамки. Отмеченные объекты меняют цвет на
красный.
После выделения объектов левой части сетки выполняется команда
Схема/Корректировка/Копировать выбранные объекты<18>. Затем
следует обращение к вкладке Копирование симметрично (кнопка
<29>*) с включением параметров Указать базовый узел и Относительно плоскости YOZ. Остается щелкнуть кнопкой мыши по крайнему правому узлу копируемой сетки, убедиться, что этот узел сменил
цвет с зеленого на розовый и выполнить команду Применить<35>*.
Видно, что выделение элементов левой части сетки исчезло, а элементы ее правой части остались отмеченными. В строке статуса (правый
нижний угол окна на рисунке) отображается число выделенных узлов/общее число узлов, и число выделенных элементов/общее число
элементов (всего должно быть 17 узлов и 16 элементов). Снять отметку можно командой Выбор/Отмена выделения<11>.
На сетке также отсутствуют номера узлов. Эти номера имеет смысл
вывести на экран. Для этого используется команда Опции/Флаги рисования<5>, открывающая окно, на котором имеются четыре вкладки. На второй вкладке слева выбирается функция включения номеров
узлов, для чего ставится галочка рядом с картинкой <31>*, и, наконец, дается команда Перерисовать<6>.
Если в расчетной схеме конструкции добавлялись узлы, то им номера придаются по умолчанию путем добавления единицы к последнему существующему номеру. Если же узлы удалялись (в том числе и
при отмене операции создания), то в нумерации появляются пропуски. Такие пропуски можно ликвидировать, выполнив команду Схема/Корректировка/Упаковка схемы<15> и подтвердив ее нажатием
кнопки <35>* (Применить).
Задача 16
159
Следующая операция – установка замкового шарнира. Шарнир при
расчете конструкций методом конечных элементов является атрибутом стержня, а не узла, поэтому если между двумя элементами имеется шарнир, то его надо отнести к какому-либо одному из соприкасающихся торцов элементов. Постановка шарнира эквивалентна устранению поворотной связи между торцом стержня, в который он вводится,
и узлом. Этого достаточно, чтобы стал возможным взаимный поворот
торцов элементов, примыкающих к рассматриваемому узлу, т. е. поворот относительно местной оси Y 1, параллельной глобальной оси Y .
Для плоской конструкции ось Y 1, как и ось Y , отображается синим
цветом. Местная ось X1 всегда направлена вдоль оси стержня. Узел,
в котором она начинается, называется начальным узлом. Для отображения местной системы координат на экране используются команда
Флаги рисования и вкладка Элементы. Затем ставится галочка у опции Местные оси стержней и нажимается кнопка Перерисовать<6>.
Ось X1 отображается зеленым цветом. Для левой полуарки она направлена вправо и вверх, для правой – влево и вверх.
Так как подготовительные операции к установке шарнира завершены, то остается шарнир задать. Это можно сделать двумя способами.
Один из них связан с открытием окна диалога по команде Жесткости/Шарниры<22>. После вызова этого окна (или до него) необходимо выделить элемент, в торце которого предполагается поставить
шарнир. Это может быть любой из двух элементов, примыкающих
к центральному узлу – например, справа от него. Затем на вкладке
Назначить шарнир включается галочка U Y для узла 2, т. е. левого узла элемента. Завершается постановка шарнира командой Применить<35>*.
Второй способ постановки шарнира требует открытия окна Выбор/Информация об узле или элементе<12>, называемого «Фонариком». Если затем щелкнуть мышью по интересующему нас элементу,
то изобразится относящаяся к этому элементу информация. Таковая
при необходимости может быть тут же откорректирована. Поправки
должны быть подтверждены командой Применить<35>*. Наконец,
как и при постановке шарнира первым способом, осуществляется переход на вкладку назначения шарнира, ставится нужная галочка и
нажимается кнопка <35>* (см. рисунок на следующей странице).
160
Расчет с помощью программы ЛИРА
Необходимо иметь в виду следующее. Встречаются задачи, при
решении которых приходится отключать не поворотную связь между торцами элементов, а линейную: например, ставится специальный
шарнир из двух параллельных стержней. Но на рисунке сетки и такой шарнир будет изображен в форме кружочка. Поэтому всегда надо
Задача 16
161
проверять правильность назначения шарнира с помощью «Фонарика».
Как выглядит окно «Фонарика» с информацией о стержне только что
было проиллюстрировано, вид окна с информацией об узле конструкции представлен ниже.
162
Расчет с помощью программы ЛИРА
Для ряда последующих операций локальные координаты не потребуется и их можно пока отключить.
Задание топологической информации завершается расстановкой
связей, т. е. указанием вида опорных устройств. В данном случае –
это опорные шарниры. Существуют различные подходы к решению
этой задачи. Например, можно сперва поставить в опорах заделки, а
затем убрать в них связи, препятствующие поворотам. Но логичнее
сразу поставить между опорными торцами крайних элементов арки
и землей по две линейные связи – вертикальную и горизонтальную.
Это можно сделать двумя способами. Применение первого из них начинается с команды Схема/Связи<19>. В появившемся окне ставятся
галочки рядом с именами X и Z координатных осей, что означает
запрет любых линейных перемещений опорного узла. Затем надо отметить (выделить) оба опорных узла, отменить выделение всех остальных элементов сетки и подать команду Принять<34>*.
Второй способ постановки опорных связей реализуется с помощью
«Фонарика». Точно так же, как было сказано выше, устанавливаются
линейные связи, но делается это для каждого опорного узла по отдельности. Поэтому отметка узлов при этом способе не требуется. Завершается постановка связей в каждом опорном узле командой Принять<34>*. После задания связей опорные узлы изменят свой цвет на
синий. И снова контроль правильности установки связей осуществляется с помощью «Фонарика».
Жесткостные характеристики арки задаются по команде Жесткости/Жесткости элементов<20> после того, как эти характеристики
описаны и элементы с одинаковыми жесткостными параметрами выделены (отмечены). Описание жесткостей начинается с нажатия на
кнопку Добавить, открывающую три вкладки. При решении данной
задачи используется первая из них: Стандартные типы сечений. Здесь
можно из набора предлагаемых типов сечений выбрать нужное, в том
числе и прямоугольное. Именно такое поперечное сечение использовалось при расчете арки в ходе решения задачи 2. Параметры этого сечения и материала конструкции вводятся после выбора на первой вкладке опции Брус. По умолчанию ЛИРА предлагает для изгибаемой стержневой конструкции конечный элемент типа 10. Проверить или изменить тип элемента можно с помощью команды Схема/Корректировка/Смена типа конечного элемента<14>. При реше-
Задача 16
163
нии данной задачи изменять тип элемента не требуется, так что убедившись, что элементы заданы правильно, надо тут же вернуться к
окну задания жесткости и ввести высоту H и ширину B прямоугольного поперечного сечения, а также модуль упругости E материала.
На значения усилий в статически определимой конструкции постоянные H, B, E никак не влияют, поэтому вполне допустимо положить
H = B = E = 1, согласившись с такими размерностями этих величин,
которые приняты программой по умолчанию. Но разумнее задавать
истинные значения исходных данных, ибо тогда ЛИРА сможет правильно вычислить не только усилия, но и перемещения. Такие значения нетрудно указать, ибо они использовались при решении задач 2
и 6. Так, l = 26 м (с. 40), H = 0, 02l = 0, 02 · 26 = 0, 52 м (с. 76),
B = ρ · H = 0, 333 · 0, 52 = 0, 17333 м (с. 76), E = 108 кН/м2 (с. 76).
Поместить же в поля ввода надо следующие данные. В поле E: 10e8; в
поле H: 0.52; в поле B: 0.17333. Остальные поля можно игнорировать.
После закрытия окна диалога по команде Применить<35>* в
списке жесткостей появляется строка Брус 17.33X52. По ней можно
щелкнуть левой кнопкой мыши, а затем выбрать в возникшем перечне
команд команду Установить как текущий тип. Введенные численные
характеристики жесткости будут приняты программой. Если же по
строке Брус 17.33X52 сделать двойной щелчок левой кнопкой мыши,
то указанные характеристики будут приняты программой сразу. Поскольку обсуждаемые параметры жесткости одинаковы для всех элементов сетки, то надо все элементы выделить (отметить) и подать
команду Назначить. Теперь всем отмеченным элементам будет назначена выбранная жесткость и выделение исчезнет.
Наступила очередь задания внешнего воздействия. Для этой цели существует команда Нагрузки/Нагрузка на узлы и элементы<21>.
Но воспользоваться этой опцией без предварительной подготовки в обсуждаемой задаче не удастся. Дело в том, что оба рассматриваемых
воздействия привязаны к точке, находящейся на оси элемента. Координаты этой точки не совпадают ни с одними из координат узлов. В
этом можно убедиться, просмотрев координаты узлов с помощью «Фонарика»<12>, либо воспользовавшись таблицей, которая вызывается
командой Окно/Интерактивные таблицы2 . Можно будет увидеть, что
2
Диалог Редактор форм, строка Узлы, кнопка Применить<35>*; затем в окне
Создание таблицы узлов – кнопка Принять<34>*.
164
Расчет с помощью программы ЛИРА
в таблице узлов координата X нигде не равна 9 (см. расчетную схему
арки на с. 40).
Существуют различные способы решения возникшей проблемы,
вплоть до смещения нагрузки в ближайший узел сетки. Однако более
естественным представляется способ введения дополнительного узла в
том месте, где приложена сосредоточенная сила. Речь идет о постановке узла, который разделит элемент с номером 6 на две части. В этом
случае потребуется указать расстояние от начального узла 1 данного
элемента до вновь создаваемого узла.
Разница абсцисс 7-го и 6-го узлов равна 9.75 − 8.125 = 1.625.
Относительное расстояние вдоль оси X от 6-го узла до силы равно
(9 − 8.125)/1.625 = 0.538. Запомнив это число, надо обратиться к команде Задать узел и перейти на вкладку Ввести узел на расстоянии L
(самая последняя вкладка). Галочка Указать узлы курсором должна
быть включена, а галочку рядом с символом L необходимо выключить. Остается в поле N набрать запомненное число 0.538 и по очереди щелкнуть мышью по узлам 6 и 7 (именно в таком порядке). На
схеме появится новый узел с номером 18. При помощи «Фонарика»
можно проверить, правильно ли определена абсцисса X вновь образованного узла. Ответ таков: X = 8.99925 м, что практически совпадает
с заданной величиной X = 9 м.
В результате только что проведенной операции появилось два новых элемента, расположенных между узлами 6 и 18 и между узлами
18 и 7. Однако прежний элемент, соединяющий узлы 6 и 7, остался на
месте. Ясно, что его надо удалить. Для этого щелчком мыши между
узлами 6 и 18 включается режим отметки стержней, после чего в появившемся списке элементов выделяется элемент 6 (в скобках после
номера элемента приводятся номера 6 и 7 инцидентных к нему узлов).
Наконец, выделенный элемент удаляется нажатием клавиши Del на
клавиатуре.
Узел создан и теперь его можно нагрузить. Следует обращение к
команде Нагрузки/Нагрузка на узлы и элементы<21>, после которой
на вкладке Нагрузки в узлах с помощью кнопки <30>* задается сосредоточенная сила3 . Система координат выбирается глобальной, направление – вдоль оси Z. В окне Параметры нагрузки задается значе3
Коричневый цвет изображений на кнопках относится к силовому и температурному воздействиям, желтый – к кинематическому, а розовый – к динамическому.
Задача 16
165
ние силы: 33.0. Надо убедиться, что ее размерность указана правильно
(кН). Положительной считается сила, направленная вертикально вниз.
Ввод подтверждается командой Применить<35>*. Наконец, выделяется узел 18 и снова нажимается та же самая кнопка <35>*. На схеме
появится изображение силы. Случается, что масштаб рисунка выбран
программой неудачно. Поправить дело можно, если дать команду Исходный размер<9>.
Для того чтобы задать равномерно распределенную нагрузку, надо
сначала, не закрывая окна Задание нагрузок, отметить элементы от
узла 18 до узла 9, а затем перейти на вкладку Нагрузка на стержни.
Далее выбирается направление Z в глобальной системе координат и
по нажатию верхней кнопки <33>* в правой части экрана, предназначенной для операций с равномерно распределенной нагрузкой, ввести
в открывшемся окне Параметры число 4.5. Этим будет указана интенсивность распределенной нагрузки в кН/м (положительна нагрузка,
направленная вниз). Завершается ввод, как и обычно, командой Применить<35>*. После этого на расчетной схеме появится изображение
распределенной нагрузки. Окно Задание нагрузок можно закрыть.
На этом задание исходных данных завершается.
16.4. Выполнение расчета. Используется команда Режим/Выполнить расчет<2>. Появляется окно, содержащее информацию о ходе
решения. В правой части схематично отображается конструкция, слева вверху – структура матрицы коэффициентов разрешающей системы уравнений (от ее вида зависит скорость и точность решения). Ниже
матрицы написаны некоторые технические детали задачи, например,
число уравнений, ориентировочное время расчета. Еще ниже размещена кнопка Отмена, по нажатию которой после некоторой паузы появляется кнопка Закрыть. Этим расчет конструкции при необходимости
прерывается. Расчет может быть приостановлен и самой программой.
В этом случае в протоколе расчета, размещенном в нижней части окна,
будет написано: Задание не выполнено, и в левом нижнем углу появится кнопка Закрыть, по нажатию которой происходит возврат к статусу
задания исходной информации. В том же протоколе при невозможности выполнения расчета содержится информация о предполагаемом
типе ошибок.
Если программа сообщит, что, по ее мнению, конструкция является
изменяемой, то пользователю надо не только убедиться в правильно-
166
Расчет с помощью программы ЛИРА
сти расстановки связей самой конструкции, но и в том, что эти связи
правильно описаны, что жесткости всех элементов заданы отличными
от нуля и что правильно назначены их (жесткостей) единицы измерения. Часто ошибка связана с тем, что неправильно указан признак
схемы. В этом случае при помощи команды Схема/Признак схемы
этот признак надо указать повторно. К распространенным относятся
также ошибки, возникающие при задании внешнего воздействия: например, нагрузка на плоскую стержневую конструкцию направляется
вдоль оси Y .
При своем первом запуске ЛИРА тестирует возможности компьютера оптимизировать использование его памяти и увеличить быстродействие. На это уходит достаточно много времени и даже при решении задачи совсем незначительной размерности приходится долго
дожидаться появления результатов расчета. У пользователя даже может возникнуть желание осуществить аварийный выход из программы. Однако надо запастись терпением, понимая, что при всех последующих запусках ЛИРЫ такой большой задержки уже не будет.
16.5. Результаты расчета. Вывод результатов расчета на экран осуществляется командой Режим/Результаты расчета<3>. При смене режима работы на экране появляется деформированная схема, однако
недеформированное очертание арки отсутствует. Его можно вызвать
по команде Схема/Исходная + деформированная<25>, позволяющей
сравнить очертания оси арки до и после нагружения. Перемещения точек оси арки очень малы по сравнению с ее генеральными размерами,
поэтому масштаб рисунка искажен. Но это даже помогает использовать рисунок для зрительного контроля полученного результата: ведь
картина перемещений должна отвечать как заданной нагрузке, так и
наложенным на конструкцию связям.
Если деформированная схема визуальную проверку выдерживает, ее можно сменить на недеформированную (Схема/Исходная схема<24>) и с помощью кнопки <26> перейти к эпюрам усилий. В
нижней части окна появится панель, на которую эпюры усилий N ,
My , Qz и выводятся.
ЛИРА изображает эпюры усилий на осевом контуре конструкции,
а не на горизонтальной оси абсцисс, как это делается при вычислениях
вручную. Надо также иметь в виду, что осевая линия арки при расчете
была заменена на вписанный в нее многоугольник, что привело к раз-
Задача 16
167
рывам на эпюрах Q и N во всех узловых точках. Однако эти разрывы
в узлах ломаной незначительны, за исключением скачка на эпюре Q в
замковом шарнире. Объясняется это исключительно правилом знаков
для поперечных сил, предлагаемым ЛИРОЙ: положительна поперечная сила, которая в конце элемента направлена в ту же сторону, что
и ось Z1. Ориентация местных систем координат для левой и правой
полуарок различна, что и привело к различным знакам поперечных
сил по обе стороны от замкового шарнира.
168
Расчет с помощью программы ЛИРА
Для приведения эпюры Q к нормальному виду (см. рисунок на
предыдущей странице) надо перейти в режим задания исходных данных (Режим/Режим создания расчетной схемы<4>) и изменить ориентацию местных осей на правой полуарке. Эти оси идентифицируются с помощью «Фонарика» и разворачиваются так, чтобы оси X1 на
элементах 9–16 сменили направление на противоположное. Используется диалоговое окно Схема/Корректировка/Местные оси стержней,
в котором выделяются элементы правой полуарки, после чего дается
команда Инверсно под надписью Изменить направление оси X1. Конечно, описанную операцию можно было бы выполнить сразу же после зеркального отражения левой части конечноэлементной сетки, что
опытный пользователь и сделал бы. Но тому, кто только приступает
к изучению ЛИРЫ, необходимо понять, что навыка правильно вводить исходные данные для расчета конструкции недостаточно – надо
еще приобрести умение истолковывать полученные результаты. Разбор ситуации с эпюрой поперечных сил как раз и способствует такому
пониманию. Он тем более полезен, что в справке программы о влиянии локальной системы координат на вид обсуждаемой эпюры ничего
не сказано.
После смены ориентации местных координат на правой части конструкции надо повторить расчет, отключить локальный базис и вернуться в режим просмотра результатов. Эпюра Q на правой полуарке
сменит знаки на обратные.
Задача 16
169
При желании с помощью флагов рисования значения усилий по
торцам каждого элемента можно вывести на экран. Достаточно на
вкладке Значения включить галочку Значения на эпюрах. Но в этом
случае ординаты эпюр в местах стыков элементов могут наложиться
друг на друга. Поэтому лучше просмотреть значения усилий по торцам элемента с помощью «Фонарика». Так, если, выделив некоторый
элемент, щелкнуть по кнопке <12>, то появится окно, в котором надо
включить галочку Эпюры. Возникнет новое окно с кнопками, носящими имена шести усилий. В плоской задаче от нуля отличаются только
три из них: Nx , Qz и My . Кнопки с тремя остальными усилиями нужно
отключить. В табличном виде обсуждаемые усилия получают с помощью интерактивных таблиц по команде Усилия (стержни).
В приводимой на следующей странице таблице сопоставляются усилия, найденные при расчете с помощью программ Excel и ЛИРА. Это
сделано для пяти характерных сечений. Индекс у символа усилия совпадает с номером узла, в котором это усилие вычисляется. Если речь
идет об усилии в сечении, находящемся в непосредственной близости
от узла i слева, то оно получает индекс i − 0, а если справа – то индекс i + 0. Можно напомнить, что узлы 1 и 17 являются опорными,
узел 9 – центральным, а в узле 18 приложена сосредоточенная сила.
Что же касается узла 14, то он выбран потому, что в нем максимален по модулю изгибающий момент на правой части арки. Видно, что
усилие M14 , найденное приближенно (ЛИРА), практически совпадает
с точным решением (Excel).
Незначительно отличаются сопоставляемые изгибающие моменты
в сечении 18: примерно на 2,7 %. Впрчем, в этом наиболее напряженном сечении достаточно близкими в обоих расчетах оказались и
остальные усилия – продольные и поперечные силы.
Значительное расхождение между точным и приближенным решением наблюдается лишь в замковом сечении арки, да и то лишь для
поперечной силы, роль которой при оценке прочности конструкции
невелика. Значения поперечной силы справа и слева от замкового шарнира должны быть одинаковыми (Q = −19, 04), тогда как ЛИРА дает
Q9−0 = −22, 67 и Q9+0 = −15, 774 . Это следствие того, что ось арки заменялась ломаной, а такая замена наиболее заметно сказывается как
4
О необходимости смены знака у поперечных сил для сечений правой полуарки
говорилось на с. 167–168.
170
Расчет с помощью программы ЛИРА
раз для сечений около замкового шарнира: ось конструкции приобретает самый большой перелом там, где касательная к оси на самом деле
должна быть горизонтальной.
Таблица 16.2
Сравниваемые
усилия
M18
M14
Q18−0
Q18+0
Q9−0
Q9+0
N1
N18−0
N18+0
N9−0
N9+0
N17
Программа
Excel
Программа
ЛИРА
71,65
-47,13
15,41
-14,34
-19,04
-19,04
-44,41
-41,73
-27,44
-30,94
-30,94
-35,65
73,58
-47,87
15,45
-14,23
-22,67
15,77
-45,08
-42,44
-28,02
-29,11
-33,36
-36,22
Список литературы
1. Гольдштейн Ю. Б. Основы механики твердого деформируемого
тела / Ю. Б. Гольдштейн. Петрозаводск: Изд–во ПетрГУ, 2005. 872 с.
2. Ю. Б. Гольдштейн. Строительная механика: Расчетные работы и методические указания для студентов-заочников специальности
"ПГС" / Петрозаводск: Изд-во ПетрГУ, 2006. - 156 С.
3. Смирнов А. Ф. Строительная механика. Стержневые системы /
А. Ф. Смирнов, А. В. Александров, Б. Я. Лащеников, Н. Н. Шапошников. М.: Стройиздат, 1981. 512 с.
4. Смирнов А. Ф. Строительная механика. Динамика и устойчивость сооружений / А. Ф. Смирнов, А. В. Александров, Б. Я. Лащеников, Н. Н. Шапошников. М.: Стройиздат, 1984. 416 с.