Решение тригонометрических уравнений
реклама

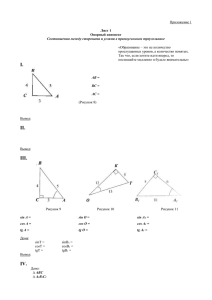
Решение тригонометрических уравнений Эпиграф урока: «Нахождение способа решения задачи подобно изобретению, а изобретение требует воображения, догадки, фантазии. Поэтому развивайте у себя эти качества». (А.И. Маркушевич) Цели консультации: Создание условий учащимся: Овладение приемами решения тригонометрических уравнений; Формирование умений отбора нужных корней уравнения на заданном промежутке, умение анализировать полученные результаты, обоснованно отбирать корни уравнения разными способами с помощью: числовой окружности, графика или решением двойных неравенств; Овладение приемами построения графика и числовой окружности. Структура консультации: 1. 2. 3. 4. 5. 6. Организационный момент. Изучение нового материала. Закрепление изученного материала. (Работа в группах). Рефлексия Итог Домашнее задание Ход урока 1. Организационный момент. Этап: инициация (приветствие, знакомство) 5 минут АМО «Поздоровайся локтями» (К.Фопель, «Сплоченность и толерантность в группе», М.: «Генезис» 2003, с 17) Цель – Встреча друг с другом, приветствие. Предварительная подготовка: Следует отставить в сторону стулья и столы, чтобы ученики могли свободно ходить по помещению. Технология проведения: Учитель просит учеников встать в круг. Затем он предлагает им рассчитаться на первый-второйтретий и сделать следующее: • Каждый «номер первый» складывает руки за головой так, чтобы локти были направлены в разные стороны; • Каждый «номер второй» упирается руками в бедра так, чтобы локти также были направлены вправо и влево; • Каждый «номер третий» нагибается вперед, кладет ладони на колени и выставляет локти в стороны. Учитель говорит учащимся, что на выполнение задания им дается только три минуты. За это время они должны поздороваться с как можно большим числом одноклассников по-английски и коснуться друг друга локтями. Через три минуты ученики собираются в три группы так, чтобы вместе оказались соответственно первые, вторые и третьи номера. После этого они приветствуют друг друга внутри своей группы. Примечание: Эта смешная игра позволяет весело начать урок, размяться перед более серьезными упражнениями, способствует установлению контакта между учениками. 2. Вводный этап. Учитель: Прежде чем вы узнаете тему сегодняшней консультации, я хотела бы продемонстрировать вам видео сюжет. http://www.youtube.com/watch?v=NgGGcuB2lrM (Ученики смотрят фильм о значении витаминов в жизни людей). Как вы думаете, почему сегодняшняя консультация началась с этого видеофрагмента? Ученики отвечают. Учитель: Действительно, мы заговорили о витаминах потому, что их названия точно такие же, как названия заданий на экзамене по математике в формате ЕГЭ 2014. Но в формате ЕГЭ 2015 задания имеют сквозную нумерацию. Номер Витамина, который мы употребим сегодня №15. Ваша задача сегодня отработать и закрепить навыки решения некоторых заданий из экзаменационного материала. Этап: формирование ожиданий обучающихся 3 мин. АМО «Импровизированные цели» (К. Фопель «Эффективный воркшоп». М.: Генезис. 2003 с.128.) Цель: выразить задачи, выяснить ожидания участников Необходимые материалы: Слайд с записанной целью урока: «Изучить способы отбора корней тригонометрических уравнений» Подготовка: на доске в середине в кругу записана цель урока. В сторонах от неё, как клумбы, изображены пустые круги или овалы. Предлагает подумать и обсудить в группах способы, над которыми будет проведена работа на уроке. Затем представители каждой группы выходят к доске и записывают сформулированные задачи в чистых кружках. Примечание: необходимо выделить небольшое количество задач. Среди них могут быть такие: «повторить методы решения тригонометрических уравнений», «изучить методы оценки» «учиться работать в группе» и т. д. Цель: научиться решать задания №15(С1) (ЕГЭ), тригонометрические уравнения, интерпретировать полученные результаты графически; отбирать корни на указанном в задании промежутке алгебраически и с помощью тригонометрического круга. 1. Актуализация Ребята получают карточку №1 - яблоко зеленое (очень полезный витамин). №1. Найдите cos , если sin = 7/25 и (0; π/2). Ответ: 0,96 № 2. Найдите значение выражения 9sin 1320 sin 2280 Ответ. – 9 № 3. Найдите cos , если sin 𝛼 = √7 4 и (0; 0,5π). Ответ. 0,75 № 4. Найдите значение выражения 50 sin 190 cos 190 sin 380 Ответ: 25 № 5. Найдите значение выражения sin70оcos40о – sin40оcos70о. Ответ. 0,5 2. Подготовительные упражнения - Рассмотреть частные случаи тригонометрических уравнений. Учащимся предлагается сопоставить уравнения и их корни. С помощью числовой окружности объяснить своё решение (указать точки, соответствующие данным корням), аналогично проанализировать свой выбор на графике соответствующих функций (слайд № 2-8). Систематизировать свои результаты в таблице. В таблице записать цвет выбранных решений. Уравнение Соответствующие точки на числовой окружности рисунок 7 Точки на графике рисунок 1 Решение cos х = 1 рисунок 8 рисунок 2 𝜋 + 𝜋𝑛, 𝑛 ∈ 𝑍 2 х = 2𝜋𝑛, 𝑛 ∈ 𝑍 cos х = −1 рисунок 9 рисунок 3 х = 𝜋 + 2𝜋𝑛, 𝑛 ∈ 𝑍 sin х = 0 рисунок 10 рисунок 4 х = 𝜋𝑛, 𝑛 ∈ 𝑍 sin х = 1 рисунок 11 рисунок 5 х= sin х = −1 рисунок 12 рисунок 6 х=− cos х = 0 х= 𝜋 + 2𝜋𝑛, 𝑛 ∈ 𝑍 2 𝜋 + 2𝜋𝑛, 𝑛 2 ∈𝑍 - разобрать пример решения тригонометрического уравнения. Ребята получают карточку №2 - яблоко красное. Приглашаются по одному представителю от группы к доске. Каждый представитель вытягивает заморочку - яблоко из бочки. Задача № 10 (тригонометрия) 1. Ответ: - 0,2. 2. 3. Найдите наименьшее значение выражения 2√3 cos 𝛽 − 2 sin 𝛽 − 6 4. Найдите tgα , если cos 𝛼 = 5√29 29 и α∈(3𝜋 ; 2π) 2 Задание 1 (Демо-версия ЕГЭ 2015) . (Слайд № 9-11). а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие промежутку . Решение: а) , откуда x= x= б) 1 способ. На рисунке 13 точками (желтыми и голубой произведен отбор корней в заданном промежутке). Рисунок 13 2 способ. График.(оранжевые точки, корни на заданном промежутке) Рисунок 14 3 способ. Решение двойных неравенств. Учитель объясняет на доске. 1) Отбор корней x= , на Так как n – целое число, то n=-2, т.е. x= 2) Отбор корней x= , для удобства разобьем решение на 2 части: Решение Решение n = -1 n = -2 Ответ: . 4. Закрепление изученного материала. (Работа в группах). В группах по 3-4 человека ученики работают над заданием 2. У каждой группы способ отбора корней определяется заранее (группа более подготовленных учащихся решают всеми тремя способами, сами определяя между участниками группы способ решения, группа экспертов будет осуществлять проверку заданий и анализировать допущенные ошибки, сверяясь с эталоном Слайдами № 13-15). Задание 2. (Слайд № 12) а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие промежутку Решение: а) Откуда x= б) 1 способ. Синяя и голубые точки изображают искомые корни. Рисунок 15 2 способ. График. Решение изображают желтые точки. Рисунок 16 3 способ. Решение неравенств. (Слайд № 15) Отбор корней x= на промежутке 3, тогда Отбор корней на промежутке Решение Решение n=-2 n=-3 Ответ: Задание 3. Группа сильных учащихся по готовому решению и эталону эксперта оценивают работы учащихся. 4. Рефлексия: группа экспертов отвечают на вопросы: Какие ошибки допустили группы? Достигнута ли цель занятия? Соответствуют ли полученные результаты исследования корней заданным промежуткам? 5. Итог урока. На данной консультации мы рассмотрели частные случаи решения тригонометрических уравнений, которые пригодились при решении более сложных уравнений. Научились отбирать корни согласно поставленной задаче. 6. Домашнее задание. Решить уравнение , на промежутке . Рефлексия: «Взгляд изнутри» Цель: Организовать рефлексию и самооценку обучающимися собственной учебной деятельности на консультации, определить домашнее задание. Происхождение метода: Необходимые материалы и условия проведения: «Барометр ожиданий и опасений», маркеры синего и красного цвета, листики синего и красного цвета. Технология проведения: Закройте глаза и мысленно вернитесь к началу урока. Вспомните все, что вы делали на уроке. Посмотрите на себя изнутри. Вы такой же, как и 45 минут назад, или чтото изменилось? (Изменились, узнали, как можно сделать отбор корней тригонометрического уравнения и создали свой кодекс дружбы, который будем стараться соблюдать). - Как бы вы теперь ответили на вопрос, подведение итогов (рефлексия, анализ и оценка урока) 5 минут АМО «Кафе» (происхождение метода: «Копилочка активных методов обучения», http://www.moi-universitet.ru/ebooks/kamo/kamo/) Цель: Выяснить получить обратную связь от учеников от прошедшего урока. Материал: скотч, цветные карточки в форме витаминок. Необходимые материалы: карточки для каждого ученика Технология проведения: Учитель предлагает ученикам представить, что сегодняшний день они провели в аптеке и теперь директор аптеки просит их ответить на несколько вопросов: - Я употребил бы еще витамины… - Больше всего мне понравилось… - Я почти усвоил… - Я перебрал… - Пожалуйста, добавьте… Участники пишут свои ответы на карточки и приклеивают на лист флипчарта, комментируя. Примечание: Для учителя этот этап очень важен, поскольку позволяет выяснить, что ребята усвоили хорошо, а на что необходимо обратить внимание на следующем уроке. Кроме того,